7. 1) Распределение по вектору скорости

Учитывая, что плотность распределения по скоростям пропорциональна плотности распределения по импульсам:

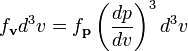
и используя мы получим:

,

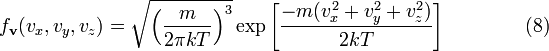что является распределением Максвелла по скоростям. Вероятность обнаружения частицы в бесконечно малом элементе около скоростиравна

2) Наиболее вероятная скорость

наиболее вероятная скорость, — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению. Чтобы найти её, необходимо вычислить, приравнять её нулю и решить относительно:

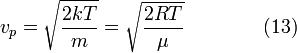
3) Средняя скорость

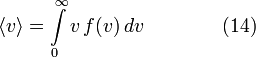
Подставляя и интегрируя, мы получим

4)Среднеквадратичная скорость

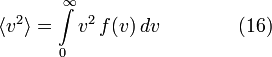
Подставляя и интегрируя, мы получим

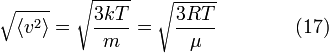
7. Основное уравнение МКТ

, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул ( в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

Вывод основного уравнения МКТ

Пусть имеется кубический сосуд с ребром длиной и одна частица массой в нём.

Обозначим скорость движения , тогда перед столкновением со стенкой сосуда импульс частицы равен , а после — , поэтому стенке передается импульс . Время, через которое частица сталкивается с одной и той же стенкой, равно .

Отсюда следует:

Так как давление , следовательно сила 

Подставив, получим: 

Преобразовав: 

Так как рассматривается кубический сосуд, то 

Отсюда:

.

Соответственно, и .

Таким образом, для большого числа частиц верно следующее: , аналогично для осей y и z.

Поскольку , то . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.

Отсюда 

или .

Пусть  — среднее значение кинетической энергии всех молекул, тогда:

, откуда, используя то, что , а , имеем .

[Править]Уравнение среднеквадратичной скорости молекулы

Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.

,

, где  — молярная масса газа

Отсюда окончательно

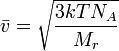
7. Теорема Больцмана о равномерном распределении кинетической энергии по степеням свободы. (Часто применяемое краткое название—теорема о равнораспределении—следует применять с осторожностью: хотя во многих случаях, как мы увидим ниже, эта теорема оказывается применимой и к потенциальной, а следовательно, и к полной энергии, но это тем опаснее, поскольку в общем случае такая теорема для потенциальных энергий не имеет места.)

Мы видели в гл. 3, 5, 7₆, что для атомов, рассматриваемых как материальные точки, движущиеся по законам классической механики, справедливо распределение Максвелла (3.1) —  (3.2) по скоростям; это справедливо как для свободных атомов (одноатомных молекул), так и для атомов, находящихся во внешних полях или даже взаимодействующих между собой не только при столкновениях (однако взаимодействие должно проявляться как наличие сил, зависящих от расстояний между атомами, а не как кинематические запреты на изменение этих расстояний, т.е. не должно быть “абсолютно жестких связей”). Из этого факта следует формула (4.3) для средней кинетической энергии атома, а с учетом изотропности распределения по скоростям получим для средней кинетической энергии, приходящейся на одну степень свободы (например, соответствующую движению какого-то атома по оси х)

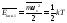. (8.1)

Общая кинетическая энергия молекулы, содержащей Z атомов, т.е. имеющей f=3Z степеней свободы, в среднем равна

. (8.2)

Формула (8.2) и выражает теорему равнораспределения для молекул, не содержащих жестких связей. Как мы покажем далее, она должна быть справедливой и в общем случае, т.е. если допустить, что f не обязательно равно 3Z.

Напомним, что числом степеней свободы системы материальных точек называют в теоретической механике число независимых переменных q_j, значениями которых можно однозначно описать любую возможную конфигурацию этих точек. Сами переменные q_j называются обобщеннымикоординатами системы, их изменение q_j=q_j(t) можно называть движением по соответствующим степеням свободы. При отсутствии жестких связей между атомами f=3Z. Наличие связей выражается “кинематическими” уравнениями между координатами атомов, например, (x₁–x₂)²+(y₁–y₂)²+(z₁–z₂)²=const.=l₁₂². Соответственно число независимых переменных будет уменьшено, f<3Z. (Во многих книгах, в частности, в [1], [16], термин “обобщенные координаты” применяется только к таким случаям; но мы будем называть обобщенными, как это часто делaют, вообще любые не-декартовы координаты, например, сферические координаты одной точки.)

Если допустить существование абсолютно жестких связей (ниже мы обсудим, можно ли считать обоснованным такое допущение, так же как и принятое выше отождествление атомов с материальными точками), то следует специально выделить случаи, когда молекулу в целом можно считать абсолютно твердым телом. Такая молекула имеет три поступательных степени свободы, описываемых координатами центра инерции(f_пост.= 3), и две или три ориентационных (они же вращательные). Если все атомы лежат на одной прямой, то вращательными координатами могут служить два угла (и ), задающих ориентацию этой прямой в сферической системе координат; в противном случае, кроме углов и для направления одной связи, надо указать еще третий угол, задающий поворот какой-либо другой связи вокруг этого направления. Поскольку для абсолютно твердого тела кинетическая энергия вращения может быть выражена как _jI_j_j² (где I_j — главные значения тензора моментов инерции , a _j — проекции вектора угловой скорости на главные оси эллипсоида инерции, см. [16], § 53), для величин _j справедливы одномерные максвелловские распределения вида (3.21), в которых роль масс играют I_j; соответственно средняя кинетическая энергия вращения 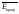оказывается равной 2·kT/2 для линейной или 3·kT/2 для нелинейной молекулы, т.е. она выражается формулой вида (8.2) соответственно с f =f_вращ.=2 или f =f_вращ.=3. Для полной кинетической энергии молекулы в обоих случаях справедливо (8.2) с f=3+ f_вращ.<3Z.

В курсах теоретической механики доказывается, что если на систему из Z материальных точек, на которые действуют силы, возникающие за счет движения внешних тел, наложено Z_связ. жестких связей, то работа этих сил отличается от их работы при действии на свободную систему в отношении (3Z–Z_связ.)/3Z, т.еf/3Z. Отсюда и следует, что формула (8.2) справедлива в самом общем случае, когда f≤3Z. Таким образом, на одну степень свободы любой молекулярной системы должна приходиться в среднем одна и та же кинетическая энергия, равная (1/2)kT.Это и есть теорема равнораспределения.

Обратите внимание на двусмысленность выражения “в среднем приходится на… (или должна приходиться на…)”. Слова “в среднем” означают, конечно, прежде всего, усреднение по флуктуациям. Однако они имеют и более глубокий смысл. Если бы кинетическая энергия разделялась на вклады, связанные с отдельными степенями свободы, то проще было бы сказать, что каждый такой вклад в среднем (по времени или по ансамблю одинаковых систем) равен (1/2)kT. Но это далеко не всегда так. В общем случае кинетическая энергия представляется квадратичной формой

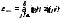.  (8.3)

[Здесь коэффициенты 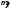, играющие в диагональных членах (приj=k) роль масс, — не обязательно константы, а являются, возможно, функциями от всех q_i :

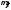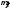=({q_i}). ]   (8.4) Если в этой квадратичной форме исчезают при каких-либо j все _jk для k≠j, то действительно можно говорить о “кинетических энергиях этих отдельных степеней свободы”. Пусть число таких выделенных “чисто диагональных” членов в сумме равно f₁ (причем три из них всегда можно связать с координатами центра инерции, но это сейчас не важно). Для остальных f– f₁ степеней свободы можно сказать только, что их общий вклад в Е_кин. в среднем равен (f– f₁)·(1/2)kT.Таким образом, более детальная формулировка теоремы гласит: средняя кинетическая энергия каждой из f₁ выделенных в указанном выше смысле (“приватизированных”) степеней свободы равна (1/2)kT; на каждую из остальных f– f₁ степеней свободы приходится в среднем такая же доля из их общей (неразделенной, “общественной”) кинетической энергии.

Мы не будем останавливаться на вопросе о корреляциях между q_iи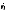, наличие которых должно следовать из распределения (7.15) с учетом (8.3) и (8.4).

₂Поступательные, вращательные и колебательные степени свободы одноатомных, двухатомных, линейных трехатомных и нелинейных многоатомных молекул. Из анализа типичных параметров атомов и молекул (который мы не будем проводить), можно убедиться, что обычно все движения молекул и атомов в них распределяются по величинам характерных скоростей (или, более точно, по характерным временам прохождения расстояний, на которых заметно изменяется потенциальная энергия, зависящая от соответствующей обобщенной координаты) следующим образом: самым медленным является поступательное движение молекул; за ним следует вращательное движение молекул, рассматриваемых как абсолютно твердые тела; самыми быстрыми являются внутримолекулярные колебания атомов за счет сил междуатомного взаимодействия. Такое соотношение типичных характерных скоростей позволяет в (обычно) удовлетворительном приближении рассматривать эти типы движений как независимые.

К такому же выводу можно прийти и из других (хотя и тесно связанных с этими) соображений. В отношении поступательного движения он следует уже из того, что кинетическая энергия любой системы материальных точек точно выражается через квадрат скорости их общего центра инерции, а потенциальная энергия во внешнем поле тяжести является медленно меняющейся функцией координат и потому практически зависит только от положения центра инерции. Отсюда следует, как уже сказано в гл. 7.₇, что скорость поступательного движения молекулы подчиняется распределению Максвелла (3.1), (3.2) с параметром   m/2 m/2kT (в последнем выражении использованы результаты, полученные в гл. 5, 6), а средняя кинетическая энергия, приходящаяся на каждую из f_пост.=3 поступательных степеней свободы дается формулой, аналогичной (8.1):

. (8.5)

Что касается потенциальной энергии, которую молекулы могут иметь за счет внешних полей, то она обычно мала по сравнению с kT, и в теории теплоемкости газов ее можно не учитывать. (Это относится и к потенциальной энергии вращательных степеней свободы, рассматриваемых ниже.) Соответственно

. (8.6)

Далее, отметим, что колебания атомов в молекуле всегда имеют малые амплитуды по сравнению с ее размерами. Поэтому, рассматривая поступательное и вращательное движение молекулы, т.е. отвлекаясь пока от внутримолекулярных движений, можно приближенно считать ее жестким (абсолютно твердым) телом, характеризующимся некоторым эллипсоидом инерции (см. [16], § 53), и связать с ней систему координат, в которой начало отсчета движется вместе с центром инерции, а оси вращаются, совпадая в каждый момент с главными осями тензора инерции.Для жесткой молекулы в энергию ее j-го состояния _jсм. гл. 7_7.; напомним, что состояния искусственно нумеровались там как дискретные) входит кинетическая энергия вращения, а в <N_j>как отдельный множитель, — плотность распределения по угловым скоростям при =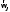. В случае двухатомной молекулы достаточно ввести двухкомпонентный вектор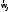, перпендикулярный мгновенному направлению оси молекулы, т.е. линии, соединяющей центры атомов (вращение вокруг этой последней оси не нужно рассматривать, если атомы считаются материальными точками). Если молекула состоит из трех или большего числа атомов, не лежащих на одной прямой, то вектор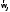— трехмерный, с компонентами, ориентированными в каждый момент параллельно главным осям тензора инерции ([16], § 53). Соответственно число вращательных степеней свободы f_вращ. равно двум или трем, и средняя кинетическая энергия, приходящаяся на каждую из них, равна той же величине (8.5). Итак, для жестких молекул

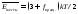. (8.7)

Формуле (8.7) соответствует молярная теплоемкость при постоянном объеме

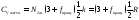. (8.8)

Если в описанной выше системе координат все атомы занимают в состоянии равновесия какие-то определенные положения, соответствующие минимуму потенциальной энергии их взаимодействия Е_пот., а при смещении атомов от этих положений Е_пот. возрастает как квадратичная функция обобщенной координаты q_j, то изменение q_j [q_j(t)=q_j(t)– q_j0, где q_j0 — значение q_jв равновесии] представляет собой гармоническое колебание; на практике это бывает справедливо почти всегда, пока амплитуды колебаний достаточно малы. Соответствующая степень свободы называется тогда колебательной. Записывая вклад q_jв потенциальную энергию молекулы как E_пот.j=q_j² и используя (7.15), мы видим, что функция распределения по q_j имеет такую же форму, как распределение Максвелла по одной компоненте скорости [ср. (7.15) для двухатомной молекулы]; следовательно, повторяя расчет, приведенный в гл. 4, мы получим аналогично (4.3):

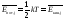(8.9)

[второе равенство — это (8.1)]. Этот результат можно получить и иначе, используя известное соотношение между кинетической и потенциальной энергиями при свободных колебаниях гармонического осциллятора. Но нельзя забывать, что формула (8.8) справедлива только при квадратичной зависимости потенциальной энергии от координаты! — (ср. ниже задачу 8.1). Для вклада одной (j-ой) колебательной степени свободы в молярную теплоемкость из (8.9) следует:

C_V кол.j= R. (8.10)

Формулы (8.9), (8.10) должны быть справедливы для всех

f_кол.= 3Z – f_пост.–f_вращ. (8.11)

колебательных степеней свободы, если колебательные движения атомов действительно возможны. Именно так и должно быть во вполне последовательной классической теории, которая не допускает существования абсолютно жестких связей между атомами. Подчеркнем, что вклады в теплоемкость, даваемые всеми степенями свободы молекул [формулы (8.8), (8.10)], не зависят от температуры. Это следствие применимости классической механики к рассматриваемым движениям.

Учитывая (8.8), (8.10), (8.11), имеем:

C_V= (3­ +f_вращ. + 2f_кол.)R/2.  (8.12)

Опыт показывает, однако, что в очень многих случаях измеренные теплоемкости соответствуют классической теории с f_кол.= 0, т.е. формуле (8.8). Можно предполагать, что молекулы некоторых веществдолжны рассматриваться как вполне жесткие. Имея это в виду, мы будем рассматривать два варианта классической теории теплоемкости: вполне последовательный (I), ведущий к (8.12), и полуэмпирический (II), в котором принимается (8.8).

₃Результаты классической теории для внутренней энергии и теплоемкости C_V. В следующей ниже таблице дан обзор результатов классической теории для простейших типов молекул в сравнении с экспериментом, относящимся к обычным температурам (~300 К). В большинстве приведенных примеров экспериментальные данные хорошо согласуются с теорией II, т.е. колебательные степени свободы не вносят вклада во внутреннюю энергию энергию и в C_V — молекулы ведут себя как жесткие; отличие в величинах  = C_p/C_V = 1+R/C_V обычно не превышает 1% (см.[1]). Несколько большие отличия от теории II, указанные в 3-й, 4-й и 6-й строках знаком > для экспериментального значения, далеко не достигают различия между теориями II и I. С ростом температуры, однако, значения C_V во всех газах начинают расти, а при значительном понижении температуры — падать, приближаясь к значению (3/2)R, которое для всех температур характерно для газов из одноатомных молекул. Иначе говоря, при очень низких температурах исчезает также и вклад вращательных степеней свободы.

Таблица 1.

Теплоемкости газов в зависимости от формы молекул

Форма молекулы Рисунок. O	Примеры	Z	Число степеней свободы					CV (идеальный газ)
			f	f пост.	fвращ.	f кол.	теор. I		теор. II	Экспер.
O	He, Ar, Hg	1	3	3	-	-	(3/2)R		(3/2)R	(3/2)R
О—О	H2, O2, HCl	2	6	3	2	1	(7/2)R		(5/2)R	(5/2)R
О—О	Cl2	2	6	3	2	1	(7/2)R		(5/2)R	>(5/2)R
О—О—О	CO2 , CS2	3	9	3	2	4	(13/2)R		(5/2)R	>(5/2)R
	H2O, D2O	3	9	3	3	3	(12/2)R		(6/2)R	(6/2)R
	Cl2O	3	9	3	3	3	(12/2)R		(6/2)R	>(6/2)R