книги / Принципы и практика решения задач по общей физике. Механика. Физика макросистем

3.3.Гармоническое движение

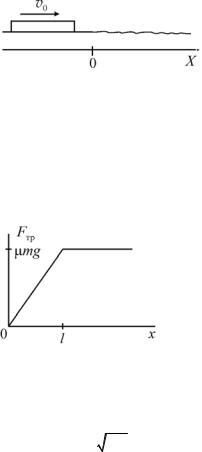
3.3.1.Полет камня в глубоком тоннеле. Через центр Земли от одного полюса к другому прорыт прямой тоннель (рис. 3.18). Пренебрегая сопротивлением воздуха, определить время полета камня от одного полюса к другому. Плотность Земли считать постоянной.

Направим ось X c началом в центре Земли вдоль тоннеля и запишем для падающего камня второй закон Ньютона:

md 22x = −F(x) , dt

где F(x) – модуль силы притяжения, кото-

рая в силу симметрии задачи может зависеть только от расстояния камня до центра Земли x . Применить закон тяготения к падающему камню напрямую нельзя, так как этот закон в его первоначальном виде справедлив толь-

ко для материальных точек. Для расчета силы тяготения разделим мысленно Землю на две части – шаровой слой с внутренним радиусом, равным x (область 1), и сфе-

ру радиусом x (область 2). Покажем, что сила взаимодействия камня и шарового слоя, как это ни парадоксально, равна нулю!

Разобьем область 1 на бесконечно тонкие шаровые слои радиусом R. Построим конус с малым углом раствора и вершиной в точке, где находится камень массой m (рис. 3.19). Сила притяжения масс m и dm1

141

dF1 = G mdm1 .

r12

Если ввести поверхностную плотность тонкого шарового слоя σ, то массу dm1 можно представить в виде dm1 =σdS1 , где dS1 – площадь участка, вырезанного конусом с одной стороны от массы m . Тогда сила

dF1 =G mσdS1 .

r12

Напрямую интегрировать это выражение по всем элементам dS1 нельзя (сила – величина векторная!), поэтому разложим

силу dF1 на две проекции: на нормаль к элементу dS1 – dF1n и на касательную – dF1τ . Величина нормальной составляющей силы

под которым видна площадка dS1 из точки, где находится масса m . Таким образом, нормальная составляющая силы тяготения

dF1n =GmσdΩ ,

причем точно такое же выражение получается и для силы dF2n (телесный угол один и тот же!). Обратимся теперь к касательной составляющей силы dF1τ :

dF1τ = Gmσ dS1 sin α1 .

r12

Представим это выражение несколько иначе:

dF1τ =GmσdS1 cos α1 tgα1 =GmσdΩtgα1.

r12

Соответственно для противоположного элемента dS2 имеем: dF2τ = GmσdΩtg α2 .

142

Так как элементы располагаются на поверхности сферы, то α1 = α2 и соответственно dF1τ = dF2τ . Если учесть, что равны и нормальные составляющие сил, то это означает, что масса m притягивается одинаково к любым двум противоположным относительно ее элементам сферического слоя (но только сферического слоя!).

Таким образом, мы доказали, что внутри любого однородного сферического слоя нет поля тяготения. С учетом доказанного утверждения сила тяготения камня обусловлена только его притяжением к шару радиусом x и массой M (x) , т.е. только к области 2:

= mM (x) F(x) G x2 .

Так как плотность Земли ρ = const , то

43 πx3ρ,

На самом деле нам не нужно знать значение плотности Земли, так как при x, равном радиусу Земли R3 , сила тяготения должна быть равна силе тяжести mg ( g – ускорение свободного падения на поверхности Земли). Окончательно

F(x) = mg x . R3

И тогда второй закон Ньютона для падающего камня приобретает вид

m d 22x = −mg x . dt R3

143

Сокращая на массу, получаем

d 22x + g x = 0 . dt R3

А это есть дифференциальное уравнение гармонических коле-

Любопытно, что это время равно половине времени обращения спутника вокруг Земли на малой высоте.

Попробуйте доказать, что столько же времени потребуется камню, чтобы показаться с другой стороны прямого тоннеля, не проходящего через центр Земли, если пренебречь вращением Земли и трением.

3.3.2. Веревка в трубе. Однородную веревку длиной l удерживают в гладком вертикальном колене изогнутой трубки так, что нижний конец веревки касается горизонтальной части трубки (рис. 3.20). Через какое время веревка полностью окажется в горизонтальном колене, если ее отпустить?

Рассмотрим произвольное положение веревки, когда она сместится на расстояние x от верхнего края трубки. Единственной внешней силой, влияющей на движение веревки, является сила тяжести, приложенная к вертикальной части веревки длиной l − x .

Так как веревка однородна, то сила тяжести

144

Таким образом, мы приходим к неоднородному дифференциальному уравнению

x + gl x = g ,

которое после замены переменных ξ = x −l , приводится к стандартному дифференциальному уравнению гармонических колебаний

ξ+ gl ξ = 0 .

Конечно, если горизонтальное колено трубки очень длинное, то ни о каких колебаниях не может быть и речи. После того, как веревка вся окажется в горизонтальном колене, она будет двигаться равномерно. Но, представим, что длина горизонтального участка трубки равна длине веревки, а затем начинается вертикальный участок. Тогда, очевидно, мы будем наблюдать колебательное движение

окажется в горизонтальном колене трубки, будет равно четверти периода этих колебаний:

Посмотрим, изменится ли ответ, если вначале часть веревки уже находится в горизонтальном колене. Конечно, нет, так как изменится только амплитуда колебаний, а период не зависит от амплитуды.

3.3.3. Брусок на шероховатой поверхности. По гладкой гори-

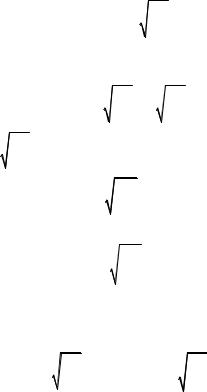
зонтальной плоскости со скоростью v0 скользит однородный брусок длиной l (рис. 3.21). Брусок наезжает на обширный шероховатый участок с коэффициентом трения µ . Через какое время брусок оста-

новится?

Если брусок принять за материальную точку, то после того, как он въедет на шероховатый участок, появится сила трения, равная µmg . Эта сила приведет к равнозамедленному движению с уско-

145

рением a =µg , и тогда время движения было бы равным t = v0 / a = = v0 / µg . Но брусок, обладающий

длиной, никак в данных условиях нельзя принять за материальную точку! Он будет въезжать на шероховатый участок постепенно, следо-

вательно, и сила трения не будет оставаться постоянной. Примем за x координату правого конца бруска. Тогда легко увидеть, что сила трения, действующая на брусок, должна иметь вид, представленный на рис. 3.22. Описать такую зависимость простой аналитической функцией нам не удастся, поэтому задачу следует разбить на два этапа.

1. Пусть длина бруска и его скорость таковы, что он остановится раньше, чем весь окажется на шероховатой по-

скорость бруска меньше некоторой минимальной скорости vmin , которую можно найти из условия

которое формально совпадает с дифференциальным уравнением гармонических колебаний, хотя, очевидно, в отличие от предыдущей

146

задачи ни о каких колебаниях не может быть и речи. Это совпадение означает только то, что характер движения бруска на этапе торможения формально похож на некоторый отдельно выбранный интервал гармонического движения. Воспользуемся тем, что мы знаем, как выглядит решение уравнения (1):

Дифференцируя это выражение по времени, найдем закон изменения скорости:

которое определяет точку остановки правого конца бруска.

Время торможения τ можно найти из условия v(τ) = 0 . Из уравнения (2) следует

Интересно, что это время никак не зависит от начальной скорости бруска.

2. Пусть теперь начальная скорость бруска больше vmin . В этом

случае брусок весь въедет на шероховатый участок и остановится, пройдя еще некоторое расстояние при постоянной силе трения µmg .

Поэтому время торможения будет складываться из двух слагаемых. Первое слагаемое равно времени, через которое брусок весь въедет

147

на шероховатый участок, – τl , и у него еще сохранится некоторая скорость vl . Второе слагаемое равно времени торможения от скорости vl до нуля при постоянной силе трения.

Найдем вначале скорость vl из теоремы об изменении кинетической энергии:

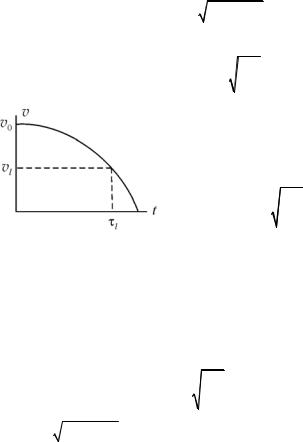
Отобразим графически этот закон изменения (рис. 3.23). Полагая v = vl , найдем время въезда бруска на шероховатую поверхность τl :

148

3.3.4. Тело на колеблющейся наклонной плоскости. На на-

клонной плоскости с углом наклона α (рис. 3.24), совершающей гармонические колебания с большой частотой ω вдоль своей поверхности, находится небольшое тело. Амплитуда скорости колебаний плоскости v0 , коэффициент трения µ . Какова средняя скорость соскальзывания тела за достаточно большое время, если tg α <<µ ?

Попробуем представить характер движения тела вдоль плоскости. Если бы плоскость не совершала никаких колебаний, то при выполнении условия tg α <<µ

(или даже более слабого условия tg α <µ )

тело вообще никуда не будет двигаться.

При наличии колебаний за счет силы трения тело будет получать небольшие импульсы противоположных направлений вдоль плоскости. Малость этих импульсов обусловлена малым временем действия силы трения (большая частота колебаний плоскости ω). Если бы плоскость была горизонтальной, то в среднем скорость движения тела при колебаниях с большой частотой была бы равна нулю. Но так как плоскость наклонена, то под действием силы тяжести возможно через достаточно большое время почти установившееся соскальзывание тела с небольшой скоростью u .

Обратимся к графику зависимости скорости колебаний плоскости v от времени t (рис. 3.25). Пусть положительное значение скорости v соответствует дви-

жению плоскости вниз, а отрицательное значение скорости v соответствует движению вверх. В связи с такой договоренностью мы должны считать и скорость почти установившегося соскальзывания тела u также положи-

тельной. Рис. 3.25

149

Понятно, что тело будет получать за счет колебаний плоскости небольшие импульсы ∆pвниз , направленные вниз, если скорость плоскости положительна (т.е. направлена вниз) и больше скорости установившегося движения тела u . Это происходит в интервале времени ∆t1 . Если же скорость колебаний плоскости меньше скорости тела u , или отрицательна (т.е. плоскость движется вверх), то тело будет получать небольшие импульсы ∆pвверх , направленные вверх. Этот интервал вре-

мени ∆t2 , как видно на рисунке, больше интервала ∆t1 . Легко сообразить, что условием «стационарности» движения тела является равенство импульсов, полученных за промежутки времени ∆t1 и ∆t2 :

∆pвниз = ∆pвверх .

Это равенство можно переписать иначе:

∆t1aвниз = ∆t2 aвверх ,

где aвниз – ускорение тела при движении плоскости вниз; aвверх – ускорение тела при движении плоскости вверх. Модули этих ускорений, как следует из второго закона Ньютона, определяются по формулам:

aвниз = g(µ+ tg α)cos α , aвверх = g(µ− tg α)cos α .

На рис. 3.25 видно, что интервал времени ∆t1 , в течение которого тело получает импульс вниз,

∆t1 = T2 − 2τ,

где T – период колебаний плоскости, равный 2π/ ω; τ – время много меньшее периода колебаний и в течение которого скорость колебаний плоскости меньше скорости установившегося движения тела u . Интервал же времени, в течение которого тело получает импульс вверх,

∆t2 = T2 + 2τ.

150