
matstatistika_1_2_3_RGR
.pdf2.2. Тема 5: Модель линейной парной регрессии y = a + bx
20 баллов
Задание расчетно-графической работы № 3.
общая сумма : 25 баллов
1.Определить (!) какой из заданных показателей является зависимой переменной, а какой – независимой.
2.Построить поле корреляции.
3.Найти точечные и интервальные оценки параметров модели y = a + bx
~ ~ ~2 |
~ |
~ |
(a,b ,σ |
, D(a), D(b)) |
|
4.Оценить значимость коэффициентов регрессии при γ = 0,95 , используя:
а) t-критерий Стьюдента;
б) доверительные интервалы истинных значений параметров.
5.Верифицировать полученную модель, используя: а) дисперсионный анализ в регрессии; б) элементы теории корреляции.
6.Интерпретировать полученные результаты.
7.В случае пригодной линейной модели построить точечные и интервальные прогнозы зависимой переменной, если ее прогнозное значение увеличится на p % от среднего (при α = 0,05).
|
|
|
|
2.2.1. Основные формулы |
||
1. Исходные данные: |
|
|
|
|
||
xi |
x1 |
x2 |
… |
|
xn |
|
yi |
y1 |
y2 |
… |
|
yn |
|
х – независимая (объясняющая) переменная или фактор, или регрессор; у – зависимая (объясняемая) переменная.
Исходные данные используются для построения линейной регрессионной модели: y = a + bx .
2. Построение поля корреляции: на координатной плоскости отмечаем точки (x1, y1), (x2 , y2 ) , …, (xn , yn ) . Затем через них проводим прямую (рис.
2.7). По расположению точек вокруг прямой определяем каким будет поле корреляции:
а) однородным – если точки расположены равноудаленно от прямой (гомоскедастичность);
б) неоднородным – если точки разбросаны неравномерно от прямой (гетероскедастичность).
51
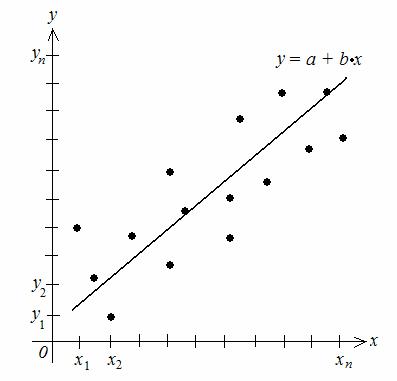
Рис. 2.7. Поле корреляции
3. Для нахождения точечных и интервальных оценок параметров модели
y = a + bx ( ~ ~ σ~2 ~ ~ ) используем метод наименьших квадратов. Для a,b , , D(a), D(b)
этого составляем и заполняем вспомогательную таблицу:
№ |
xi |
yi |
x2 |
y2 |
xi yi |
|
|
|
i |
i |
|
1 |
x |
y1 |
|
|
|
|
1 |
|
|
|
|
2 |
x2 |
y2 |
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
п |
xn |
yn |
|
|
|
Итого |
Σ=… |
Σ=… |
Σ=… |
Σ=… |
Σ=… |
Оценки параметров модели находятся по формулам: |
|
|
|
|||||||||||
a |
= |
∑x2 |
∑ y |
|
− ∑x ∑x y |
, |
~ |
= |
n∑x y |
− ∑x |
∑ y |
|
, |
|
i |
|
i |
i i i |
b |
|
i i |
i |
|
i |
|||||
~ |
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
k |
|
|
|
|
|
k |
|
|
|
|
|
|
|
k = n∑xi2 −(∑xi )2 , |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
n – количество наблюдений. |
|
~ |
~ |
|
|
|
|
|
|
|||||
Уравнение прямой линии примет вид: |
|
|
|
|
|
|
|
|||||||
y = a + b x . |
|
|
|
|
|
|||||||||
(2.1)
(2.2)
Для анализа полученной модели рассчитываем теоретические значения объясняемой переменной:
~ ~ |
~ |
(2.3) |
yi = a |
+ b xi . |
52

|
№ |
|
yi |
|
~ |
|
|
~ |
|
~ |
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
yi |
~ |
|
yi − yi |
|
(yi − yi |
) |
|
||
|
1 |
|
y1 |
~ |
~ |
|
|
|
|
|
|
|
|
|
y1 |
= a |
+ b x1 |
|
|
|
|
|
|
||
|
2 |
|
y2 |
~ |
~ |
~ |
|
|
|
|
|
|
|
|
y2 |
= a |
+b x2 |
|
|
|
|
|
|
||
|
… |
|
|
~ |
~ |
~ |
|
|
|
|
|
|
|
п |
|
yn |
|
|
|
|
|
|
|||
|
|
yn |
= a |
+b xn |
|
|
|
|
|
|
||
|
Итого |
|
Σ=… |
|
– |
|
|
Σ=…≈0 |
|
Σ=… |
|
|
Величины ei = yi − ~yi , i =1,2,...,n называются остатками регрессии (разница между фактическими и теоретическими значениями объясняемой перемен-
n
ной). ∑ei ≈ 0.
i=1
Находим остаточную сумму квадратов
|
|
|
|
|
n |
|
2 |
n |
~ 2 |
|
|
|
|
(2.4) |
||||
|
|
|
|
|
Rmin = ∑ |
(ei ) |
= ∑(yi − yi ) . |
|
|
|
|
|||||||
|
|
|
|
|
i=1 |
|
|
|
i=1 |
|
~ |
|
~ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Несмещенные оценки дисперсий и ковариаций оценок a |
и b |
определяем |
||||||||||||||||
по формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ ~ |
∑xi2 |
|
Rmin |
~ ~ |
n |
|
Rmin |
~ ~ |
− ∑xi |
|
Rmin |
|
|
|
||||
D(a )= |
k |
|
|
; |
D(b )= k |
|
|
; |
cov(a,b )= |
k |
|
|
(2.5) |
|||||
n − 2 |
n − 2 |
n − 2 |
||||||||||||||||
Несмещенной оценкой дисперсии ошибок наблюдений будет S |
2 |
|
~2 |
|
Rmin |
|||||||||||||
|
=σ |
= |
|
. |
||||||||||||||
|
n − 2 |
|||||||||||||||||
4) Оценка значимости коэффициентов регрессии при γ = 0,95
а) доверительные интервалы истинных значений параметров
Находим интервальные оценки или доверительные интервалы для полученных коэффициентов регрессии:
~ |
~ ~ |
|
|
|
~ |
+ tγ |
~ ~ |
~ |
~ ~ |
~ |
~ ~ |
(2.6) |
a −tγ |
D(a )< a |
< a |
D(a ), |
b −tγ |
D(b ) |
<b <b + tγ |
D(b ), |
|||||
|
1 |
+ |
γ |
|
|
– квантиль |
t -распределения |
(распределения |
||||
где tγ =tγ (n − 2) =t |
2 |
|
,n − 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Стьюдента) уровня |
1+γ |
и числа степеней свободы n − 2 (значение t |
опреде- |
|||||||||
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ляется как в теме 2). γ – доверительная вероятность или надежность (дана в за-
дании).
Если доверительный интервал для данного коэффициента регрессии содержит нулевое значение, то этот коэффициент считается статистически незначимым.
Б) t-критерий Стьюдента
Далее проверяем гипотезу |
H0 : a = 0 |
против альтернативной |
гипотезы |
|||
H1 :a ≠ 0, используя при этом статистику |
|
|
|
|||
t |
|
|
~ |
t |
, |
(2.7) |
0a |
= |
a − 0 |
||||
|
|
~ ~ |
γ |
|
|
|
|
|
|
D(a ) |
|
|
|
t0 – наблюдаемое или экспериментальное значение t -статистики.
53
Гипотеза H0 отвергается (и принимается H1), если t0 >tγ (это означает, что параметр а – значим). В противном случае гипотезу H0 следует принять, т.е. считать, что результаты наблюдений согласуются с гипотезой H0 , не противоречат ей (это означает, что параметр а – незначим).
Аналогично проверяются гипотезы |
H0 :b = 0 и |
H1 :b ≠ 0, используется |
|||||
критерий, статистика которого |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
0b |
= b − 0 |
t |
|
. |
|
(2.8) |
|
~ ~ |
γ |
|
|
|
||
|
|
D(b ) |
|
|
|
|
|
5. Верификация модели |
|
|
~ |
|
~ |
|
|
|
|
|
|
или ее верификация, а также |
|||
Пригодность построенной модели y = a |
+ b x |
||||||
качество оценивания регрессии может быть проверено двумя равноценными способами: дисперсионным анализом в регрессии и с использованием элементов теории корреляции.
а) Дисперсионный анализ в регрессии
Суть метода заключается в разложении общей суммарной дисперсии выходной величины y на составляющие, обусловленные действием входных пе-
ременных-факторов, и остаточную дисперсию, обусловленную ошибкой или всеми неучтенными в данной модели переменными. Фактор оказывает несущественное влияние на y , если соответствующая ему дисперсия и дисперсия
ошибок статистически незначимы. Для проверки гипотезы о равенстве таких дисперсий используется критерий Фишера (F-критерий). Поскольку для оценок дисперсий используются суммы квадратов SS (от англ. sum of squares) отклонений значений данной переменной от ее средней величины, то можно говорить о разложении общей суммы квадратов SSобщ. на составляющие.
|
|
SSобщ. = Σ(yi − y)2 |
(2.9) |
|||||
– величина, характеризующая разброс значений yi |
относительно среднего зна- |
|||||||
чения y ( y = |
1 |
n |
|
|
|
|
||
|
∑ yi ). Разобьем эту сумму на две части: объясненную регресси- |
|||||||
|
n i=1 |
|
|
|
|
|||
онным уравнением и не объясненную (т. е. связанную с ошибками εi ): |
||||||||
|
|
~ |
|
2 |
|
(2.10) |
||
|
|
SSR = Σ(yi − y) |
||||||
– сумма квадратов, объясненная регрессией, |
|
|||||||
|
|
|
|
|
~ 2 |
|
(2.11) |
|
|
|
SSост. = Σ(yi − yi ) |
||||||
– остаточная сумма квадратов, обусловленная ошибкой. |
||||||||
Проверка: SSобщ. = SSR + SSост. !!! |
|
|
|
|
||||
Коэффициентом детерминации, или |
долей объясненной дисперсии y , на- |
|||||||
зывается |
|
|
SSост. |
|
|
SSR |
|
|
|
|
R2 =1− |
= |
|
. |
(2.12) |
||
|
|
|
|
|||||
|
|
|
SSобщ. |
|
SSобщ. |
|
||
54

В силу определения 0 ≤ R2 ≤1. Если R2 = 0, то это значит, что регрессия ничего не дает, т. е. фактор x не улучшает качество предсказания yi по срав-
~ =
нению с тривиальным предсказанием yi y
.
Другой крайний случай R2 =1 означает точную подгонку: все наблюдаемые значения (xi , yi ) лежат на регрессионной прямой (все остатки ei = 0 ). Чем
ближе к 1 значение R2 , тем лучше качество подгонки или качество регрессии, ~y более точно аппроксимирует y .
Коэффициент R2 *100% показывает на сколько % линейная регрессия y на x объясняет дисперсию y . Остальные (1 – R2 )*100% приходятся на долю
прочих факторов, не учтенных в уравнении регрессии.
Гипотеза об отсутствии линейной функциональной связи между x и y может быть записана как H0 : b = 0 . Критерий, статистика которого распределена по закону Стьюдента, эквивалентен здесь критерию, статистика которого
F = |
MSR |
= |
SSR /1 |
F (α,1,n − 2) |
(2.13) |
|
|
||||
0 |
MSост. |
|
SSост. /(n − 2) |
кр |
|
распределена по закону Фишера со степенями свободы (1,n −2). Здесь через
MSR и MSост. обозначены средние квадраты (от англ. mean of squares), которые дают несмещенные оценки соответствующих теоретических дисперсий.
Вычисления, необходимые для дисперсионного анализа уравнения регрессии, сводят в таблицу
Дисперсионный анализ одномерной регрессии
Источник |
Число |
Сумма |
Средний |
Критерий |
Критическая |
Гипотеза |
|||||||
дисперсии |
степеней |
квадратов |
квадрат |
Фишера |
точка |
H0 :b = 0 |
|||||||
|
свободы |
SS |
MS |
|
F |
Fкр. = F(α;1,n − 2) |
|
||||||
|
|
|
|
|
|
|
|
|
0 |
F |
=… |
|
|
Регрессор |
|
|
MSR = |
SSR |
F0 |
= |
|
MSR |
Принять |
||||
x |
1 |
SSR |
|
|
|
|
|
кр. |
|
или от- |
|||
1 |
|
|
MSост. |
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
клонить |
Ошибка |
n − 2 |
SSост. |
MSост. = |
|
SSост. |
|
|
|
|
|
|
|
|
(остаток) |
|
n − 2 |
|
|
− |
− |
− |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общая |
n −1 |
SSобщ. |
|
|
|
|
|
|
|
|
|
|
|
дисперсия |
− |
|
|
|
|
|
− |
− |
− |
||||
(итог) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
при заданном уровне значимости |
|
α наблюдаемое значение F - |
||||||||||
статистики больше критической точки F0 > Fкр , то гипотеза H0 :b = 0 отвергается, то есть связь между x и y есть, и результаты наблюдений не противоречат предположению о ее линейности. В противном случае H0 :b = 0 принима-
ется и постулируется отсутствие значимой функциональной связи между x и y .
б) Использование элементов теории корреляции
55

Другой способ верификации линейной модели состоит в использовании элементов теории корреляции. Мерой линейной связи двух величин является коэффициент корреляции:
~ |
= |
nΣxi yi − ΣxiΣyi |
. |
(2.14) |
rB = r |
[nΣxi2 − (Σxi )2 ][nΣyi2 − (Σyi )2 |
|||
|
|
] |
|
Значения коэффициента корреляции принадлежат промежутку [−1;1]. Чем больше его абсолютное значение к 1, тем теснее связь между признаками. Положительная величина коэффициента корреляции свидетельствует о прямой связи между ними, отрицательная – о наличии обратной связи между призна-
ками. Также R2 = r 2 . |
|
|
|
|
|
|
B |
|
|
|
|
x и y |
|
Проверяем гипотезу об отсутствии |
|
|
линейной связи между |
|||
H0 : rB = 0 с помощью критерия Стьюдента |
|
|
|
|
|
|
t0r = rB n − 2 |
~ tγ . |
|
(2.15) |
|||
1− r 2 |
|
|
|
|
|
|
B |
|
|
|
|
|
|
6. Интерпретация уравнения регрессии |
|
|
|
|
|
|
Для линейного уравнения y = a + bx эластичность |
|
|||||
Ex (y) = |
bx |
|
|
|
(2.16) |
|
y |
|
|
||||
|
|
|
|
|||
(полученное значение будет сразу в %). x = |
1 |
n |
. Эластичность приближенно |
|||
|
|
∑xi |
||||
|
|
n i=1 |
|
|
||
показывает, на сколько процентов изменится у при изменении х на 1 % от сред-
него значения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Прогноз на основе линейной модели |
|
|
|
|
|
|
||||||||||||||
В случае точечного прогноза мы определяем |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
~ |
|
|
~ |
~ |
|
|
|
|
|
|
(2.17) |
|||
|
|
|
|
|
|
|
y0 |
= a |
+ b x0 . |
|
|
|
|
|
||||||
Так как |
прогнозное |
значение |
|
независимой |
переменной |
изменяется на |
||||||||||||||
± P% от среднего, |
|
|
|
P% |
|
|
|
|
|
|
|
|
|
P% |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x0 |
= x 1+ |
|
|
|
|
, x0 |
|
= x 1 |
− |
|
|
|
. |
(2.18) |
||||
|
|
|
|
|
2 |
100% |
||||||||||||||
|
|
1 |
|
|
100% |
|
~ |
|
|
|
|
|||||||||
Вычислим дисперсию величины |
: |
|
|
|
|
|
|
|
|
|||||||||||
y0 |
(x − x0 )2 |
|
|
|||||||||||||||||
|
|
|
|
~ |
~2 |
|
1 |
|
|
|
|
|||||||||
|
|
|
D(y0 )=σ |
|
|
+ |
|
|
|
|
|
. |
|
(2.19) |
||||||
|
|
|
|
Σ(xi − x)2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||
Отсюда видно, что дисперсия прогноза возрастает по мере удаления значе- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
~ |
ния x0 от среднего x , использованного для расчета a и b . Для расчета D(y0 ) |
||||||||||||||||||||
составить вспомогательную таблицу: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
№ |
|
xi |
xi − xi |
|
|
(x − x )2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
56

1 |
x1 |
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
п |
xn |
|
|
|
|
|
|
Итого |
Σ=… |
|
|
Σ=… |
|
|
|
Тогда доверительный интервал для прогностического значения |
|||||||
записать в виде |
|
~ |
~ |
|
~ |
||
|
~ |
−tγ |
+ tγ |
||||
|
|
y0 |
D(y0 ) < y < y0 |
D(y0 ) , |
|||
где tγ уже найдена в предыдущих пунктах.
2.2.2. Вычисления в MS Excel
y0 можно
(2.20)
Пример 6. Выполнение расчетов в MS Excel. Известны следующие данные по одному из субъектов Российской Федерации:
Совокупные до- |
|
|
|
|
|
|
|
|
ходы физ. лиц, |
|
|
|
|
|
|
|
|
млн. руб. |
14855,30 |
18745,10 |
20268,70 |
20319,30 |
20174,80 |
22524,50 |
21805,80 |
|
Вклады физ. лиц в |
|
|
|
|
|
|
|
|
банках, тыс. руб. |
36 643 |
38 297 |
38 993 |
40 394 |
41 090 |
42 691 |
43 916 |
|
|
|
|
|
|
|
|
|
|
Совокупные до- |
|
|
|
|
|
|
|
|
ходы физ. лиц, |
21571,30 |
22902,80 |
23928,40 |
23741,80 |
30271,90 |
30481,90 |
33088,00 |
|
млн. руб. |
|
|||||||
Вклады физ. лиц в |
|
|
|
|
|
|
|
|
банках, тыс. руб. |
43 988 |
44 684 |
43 721 |
44 198 |
46 465 |
47 481 |
48 438 |
|
|
|
|
|
|
|
|
|
|
Совокупные до- |
|
|
|
|
|
|
|
|
ходы физ. лиц, |
32133,70 |
34915,70 |
33377,50 |
34923,40 |
32558,70 |
33149,40 |
|
|
млн. руб. |
|
|
||||||
Вклады физ. лиц в |
|
|
|
|
|
|
|
|
банках, тыс. руб. |
49 632 |
53 506 |
52 559 |
53 461 |
49 484 |
48 387 |
|
|
1 этап. Спецификация модели. Определим, какой из заданных показателей будет зависимой переменной, а какой – независимой. Так как сбережения в банках – это часть дохода, то совокупные доходы физических лиц обозначим в качестве независимой переменной x , а вклады в банках – y .
Занесем исходные данные в MS Excel в виде таблицы, состоящей их двух столбцов, в первом расположены значения независимой переменной x , а во втором – зависимой переменной y (рис. 2.8). Чтобы определить характер зави-
симости – построим поле корреляции. Для этого выделяем оба столбца ((!) данные x должны быть в первом столбце, y – во втором), вызываем мастера диа-
грамм и выбираем точечную диаграмму (рис. 2.9). Затем проходим все шаги построения диаграммы, заполняя графы с ее названием и подписями осей координат. Получаем поле корреляции, не очень удачно расположенное на диаграмме (рис. 2.10).
57
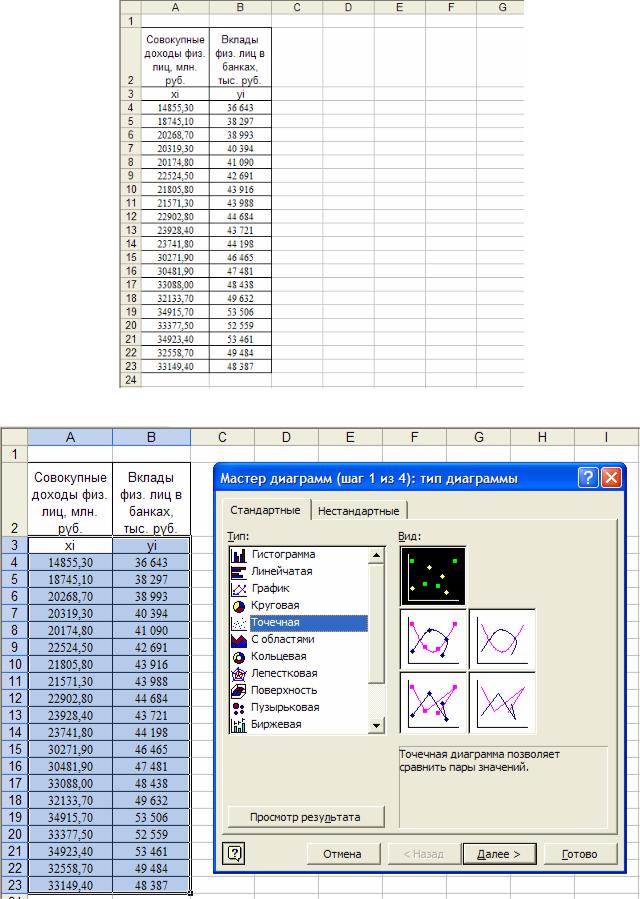
Рис. 2.8. Исходные данные в MS Excel
Рис. 2.9. Построение поле корреляции с использованием точечной диаграммы
58
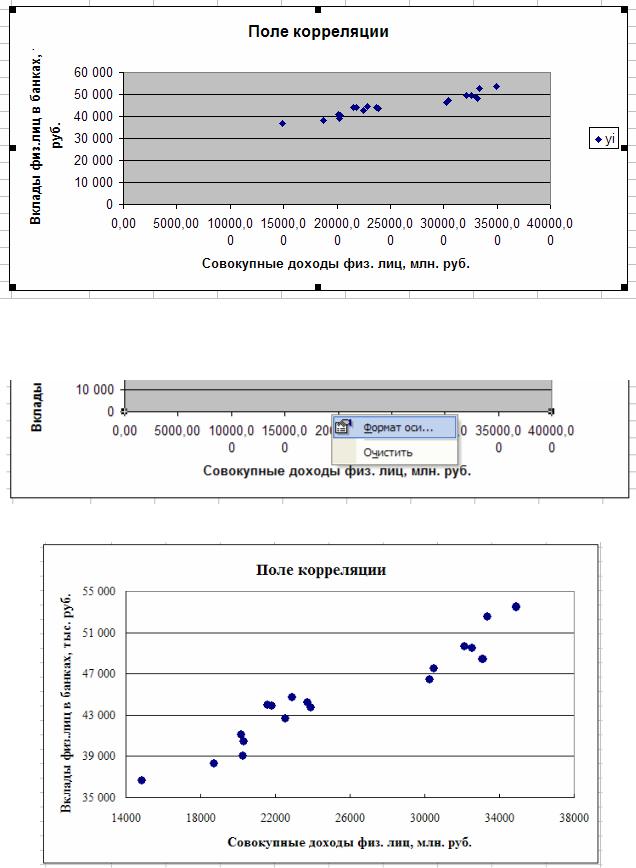
Рис. 2.10. Поле корреляции, требующее дополнительной художественной обработки
Рис. 2.11. Корректируем формат оси категорий ( x )
Рис. 2.12. Измененное поле корреляции
Мы видим, что точки близко расположены друг к другу и занимают малую часть поля диаграммы. Для этого изменим масштаб осей координат (рис. 2.11) следующим образом: подсвечиваем ось категорий (осьx ), с помощью правой
59
кнопки мыши выбираем «формат оси» и на вкладке «шкала» устанавливаем минимальное значение 14000. Аналогично на оси значений (ось y ) задаем ми-
нимальное значение 35000. Далее, используя художественные способности, облагораживаем внешний вид поля корреляции (рис. 2.12).
Следующим шагом наносим на поле корреляции прямую y = a + bx : выби-
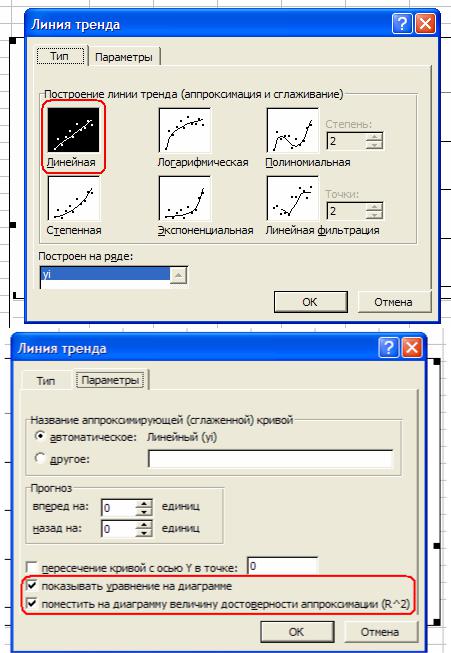
раем в меню «диаграмма» пункт «добавить линию тренда» (предварительно подсветив график) (рис. 2.13). В появившемся окошке выделяем линейную модель, затем выбираем вкладку параметры и отмечаем галочкой «показывать уравнения на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации (R^2)».
Рис. 2.13. Добавление на диаграмму прямой y = a + bx
После проведенной процедуры поле корреляции примет нужный для дальнейшего анализа вид (рис. 2.14).
60
