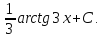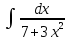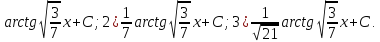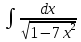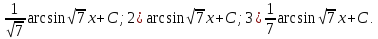- •Программированное пособие
- •Тема №1 Непосредственное интегрирование
- •Задания для самостоятельной работы
- •Тема №2 Интегрирование способом подстановки
- •Задание для самостоятельной работы
- •Задание для самостоятельной работы
- •Тема №3 Интегрирование по частям
- •I группа:
- •III группа: .
- •Задание для самостоятельной работы
- •Указания к ответам
Задание для самостоятельной работы
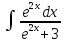 ;
2.
;
2.
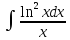 ;
3.
;
3.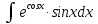 ;
;
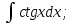 5.
5.
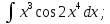 6.
6.
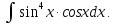
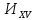
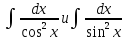
К
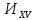 приводятся интегралы, содержащие в
знаменателе
приводятся интегралы, содержащие в
знаменателе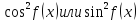 ,
поэтомуf(x)
заменяется через вспомогательное
переменное.
,
поэтомуf(x)
заменяется через вспомогательное
переменное.
Пример
1.
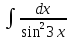 .Произведем
замену: 3x=t;
3dx=dt
.Произведем
замену: 3x=t;
3dx=dt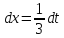 .
.
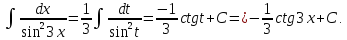
Пример
2.
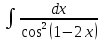 .Произведем
замену: 1-2x=t;
-2dx=dt;
.Произведем
замену: 1-2x=t;
-2dx=dt;
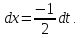
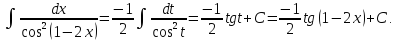
Пример
3.
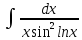 .
Произведем замену: lnx=t;
.
Произведем замену: lnx=t;
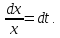
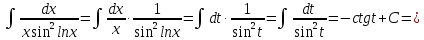
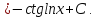
Пример
4.
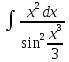 .Произведем
замену:
.Произведем
замену:
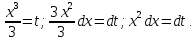
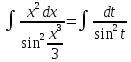 =
-ctgt+C=-ctg
=
-ctgt+C=-ctg
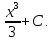
Задание №15.
|
№ |
ЗАДАНИЕ |
ВАРИАНТЫ ОТВЕТА |
|
1. |
|
|
|
2. |
|
1) |
|
3. |
|
1) |
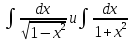
К
 приводятся интегралы, содержащие в
знаменателе корень их разности постоянной
величины и квадрата х с некоторым
коэффициентом или сумму постоянной
величины и квадрата х с коэффициентом.
приводятся интегралы, содержащие в
знаменателе корень их разности постоянной
величины и квадрата х с некоторым
коэффициентом или сумму постоянной
величины и квадрата х с коэффициентом.
Пример
1.
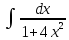 .
Произведем замену:
.
Произведем замену:
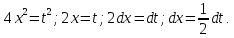
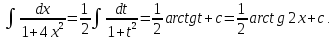
Пример
2.
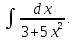 Произведем замену:
Произведем замену:
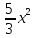 =
=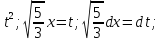
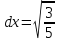 dt.
dt.
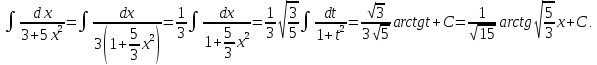
Пример
3.
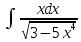 .
Произведем
замену:
.
Произведем
замену:
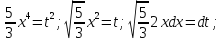
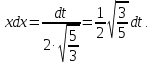
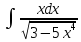 =
=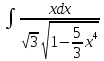 =
=
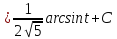 =
=
Задание №16.
|
№ |
ЗАДАНИЕ |
ВАРИАНТЫ ОТВЕТА |
|
1. |
|
1)arctg3x+C;
2) |
|
2. |
|
1) |
|
3. |
|
1) |
Задание для самостоятельной работы
4.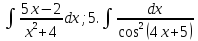 ;
6.
;
6.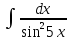 .
.
Тема №3 Интегрирование по частям
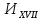
 Пусть
U=U(x)
и V=V(x)
– дифференцируемые функции. По свойству
дифференциала d(U·V)=VdU+UdV
UdV=d(U·V)-VdU.
Пусть
U=U(x)
и V=V(x)
– дифференцируемые функции. По свойству
дифференциала d(U·V)=VdU+UdV
UdV=d(U·V)-VdU.
Интегрируем
обе части равенства:
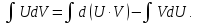
Используя свойства неопределенного интеграла, получаем формулу интегрирования по частям для неопределенного интеграла:
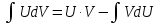
При
её применении фиксируется разбиение
подынтегрального выражения искомого
интеграла на два сомножителя U
и dV.
При переходе к правой части формулы
первый из сомножителей дифференцируется
(при нахождении дифференциала dU=U´dx),
второй интегрируется (V=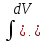
Возможности применения формулы интегрирования по частям связаны с тем, что дифференцирование может существенно упростить один из сомножителей (при условии, что интегрирование не слишком усложнит другой).
Пример
1.
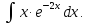
Так
как x´=1,
а
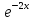 при интегрировании практически не
изменяется (появляется лишь постоянный
множитель
при интегрировании практически не
изменяется (появляется лишь постоянный
множитель ,
то данный интеграл можно найти
интегрированием по частям.
,
то данный интеграл можно найти
интегрированием по частям.

 Пусть
U=x;
dV=
Пусть
U=x;
dV=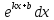 ,
тогдаdU=dx;
,
тогдаdU=dx;
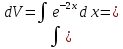 k=-2;
b=0
=-
k=-2;
b=0
=-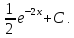
Применяя формулу интегрирования по частям, получаем:
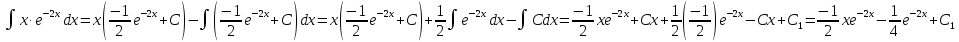
Замечание: Анализ полученного решения показывает, что постоянная С, возникшая при нахождении V (по заданному dV), не входит в запись окончательного ответа. Аналогично, в общем случае постоянная С, возникшая при нахождении V, исключается в процессе решения. Поэтому в дальнейшем, применяя формулу интегрирования по частям и найдя V, будем полагать С=0, что несколько упрощает запись решения.
Пример
2.
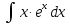 .
.
Пусть
U=x;
dV=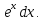
Тогда
dU=dx;
V=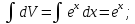
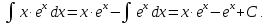
Пример
3.
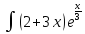 dx.
dx.
Пусть
U=2+3x;
dV=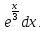
Тогда
dU=d(2+3x)=(2+3x)´dx=3dx;
V=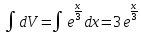 .
.
Применяя формулу интегрирования по частям, получаем:
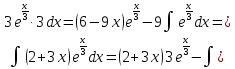
 =
=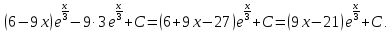
 Пример
4.
Пример
4.
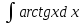
U dV
Пусть arctgx=U; dx=dV
Тогда
dU=(arctgx)´dx=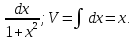
Получаем согласно формулы интегрирования по частям:
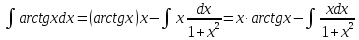 =
=
=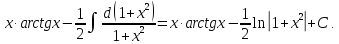
Указание. Все интегралы, которые находят с использованием формулы интегрирования по частям, можно разбить на три группы.

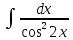
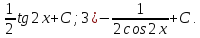
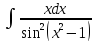
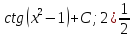 tg
tg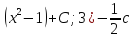 tg
tg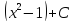
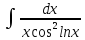
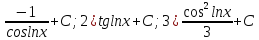
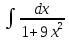
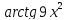 +C;
3)
+C;
3)