Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный Технический Университет Харьковский Политехнический Институт

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Дифференциальное исчисление_эл.учебник

.pdf

Скачиваний:

Добавлен:

07.03.2015

Размер:

1.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

зультатов исследования:

x		( , 2)	–2		( 2, 0)	0		(0, 2)	2	(2, )

y		+	0		–			–	0	+

y			–4 (max)						4 (min)
			–4 (max)						4 (min)

	Следовательно, функция возрастает на интервалах ( , 2)						и (2, ) , убывает на интервалах			( 2, 0) и
(0, 2) . При переходе через точку x 2				производная меняет знак «+» на знак «–», следовательно, точка x 2

является точкой максимума. При переходе через точку x 2 производная меняет знак «–» на «+», следователь-

но, x 2 – точка минимума.

Теорема 2.14 (второе достаточное условие экстремума).

Пусть функция y f (x) дифференцируема в некоторой окрестности точ-

ки x0 , имеет вторую производную в самой точке x0 и f				0	,	f
ки x0 , имеет вторую производную в самой точке x0 и f			(x0 )	0	,	f	(x0 ) 0, то-
гда функция y f (x) в точке x0 имеет экстремум, причем, если								, то –
						f	(x0 ) 0	, то –

минимум, если же f (x0 ) 0 , то – максимум.
Пример 2.32. Найти точки экстремума функции y 2x3 9x2		12x 17.
Решение. Найдем точки, в которых первая производная равна нулю:
	y 6x2 18x 12 0 x2 3x 2 0,	x 2,	x 1 .
		1	2
Вычислим вторую производную в полученных точках: y 12x 18;
y (1) 6,	x 1 – точка максимума;
y (2) 6,	x 2 – точка минимума.

Второе достаточное условие применимо реже, ибо требует существова-

ния первой и второй производной в соответствующей точке. Его нельзя приме-

нить для случая, когда в точке не существует первая производная.

Может случиться, что производные первого, второго, третьего и т.д. по-

рядков обращаются в нуль. Возможность проверить функцию на экстремум в указанных случаях дает следующая теорема.

Теорема 2.15. Пусть функция y f (x) имеет в точке x0 все производные

до n -го порядка, причем f (x0 ) f (x0 ) ... f (n 1) (x0 ) 0 , f (n) (x0 ) 0. Тогда

1)при n 2k 1 экстремума нет;

2)при n 2k есть экстремум; если f (n) (x0 ) 0 , то функция имеет мини-

мум, если же f (n) (x0 ) 0 , то максимум.

2.11.2. Наибольшее и наименьшее значения функции

Пусть функция y f (x) непрерывна на замкнутом интервале a,b . По теореме 1.18 она принимает на этом интервале свои наибольшее и наименьшее значения.

Наибольшее значение на a,b функция принимает либо в точках макси-

мума, либо на концах интервала. Наименьшее значение на a,b функция при-

нимает либо в точках минимума, либо на концах интервала.

При вычислении наибольшего и наименьшего значений функции на a,b

можно не находить точек экстремума, а поступить гораздо проще:

1)найти все критические точки первого рода, принадлежащие интервалу

a,b ;

2)вычислить значения функции в найденных критических точках и на концах интервала;

3)сравнивая полученные результаты, выбрать наибольшее и наименьшее значения функции.

Пример 2.33. Найти наибольшее и наименьшее значения функции				y	x3	5	x2	6x 5	на интервале
Пример 2.33. Найти наибольшее и наименьшее значения функции				y			x2	6x 5	на интервале
				3		2
0, 4 .
Решение.
1) найдем критические точки:
y x2 5x 6 ,	x2 5x 6 0 x 2, x 3		;
	1	2

2) вычислим значения функции в критических точках и на концах интервала:

y(2)	8	10 12 5			29	,	y(3) 9		45	18 5		19		,
y(2)		10 12 5				,	y(3) 9		2	18 5			2	,
3		3							2				2
y(0) 5		, y(4)	64	40 24 5				31	;
y(0) 5		, y(4)		40 24 5					;
		3					3
3) сравнивая найденные значения, получаем: y															31	, y		5.
3) сравнивая найденные значения, получаем: y											наиб.			3		, y	наим.	5.
											наиб.						наим.

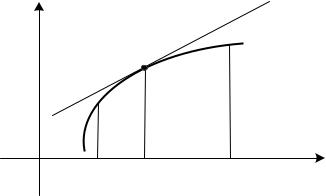
2.11.3. Выпуклость и вогнутость графика функции. Точки перегиба

Определение. График функции y f (x) называется выпуклым (вогну-

тым) на интервале a, b , если он полностью расположен под (над) касатель-

ной, проведенной в произвольной точке x0 (a,b).

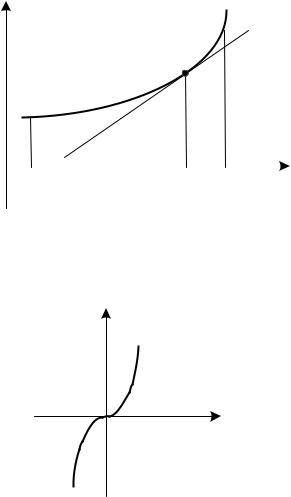
На рис. 2.18 изображен выпуклый график функции y f (x) , а на рис.

2.19 – вогнутый.

Определение. Точка кривой, разделяющая интервалы выпуклости и во-

гнутости кривой, называется точкой перегиба.

На рис. 2.20 изображен график функции y x3 , имеющий перегиб в точке x 0 .

							ая
						н
					ь
				л
			е
		т
	са
а
к

y f (x)

Рисунок 2.18

y	y f (x)

	я
	а
	льн
	е
	т
	а
	с
	ка

0 a	x0 b x

Рисунок 2.19

y x3

0 x

Рисунок 2.20

Теорема 2.16 (достаточное условие выпуклости и вогнутости графика функций). Пусть функция y f (x) имеет вторую производную на интервале

a, b , тогда:

1) если		, x (a,b) , то график функции на интервале	a, b вы-
	f (x) 0

пуклый;

2)	если		,	x (a,b) , то график функции на интервале	a, b во-
		f (x) 0
гнутый.

Теорема 2.17 (необходимое условие перегиба графика функции).

Пусть x0 – точка перегиба графика функции y f (x) . Тогда
Пусть x0 – точка перегиба графика функции y f (x) . Тогда	f (x0 ) 0
либо не существует.
74

Таким образом, для отыскания точек перегиба графика функции y f (x)

нужно рассмотреть все корни уравнения
нужно рассмотреть все корни уравнения	f (x) 0, а также точки, в которых

f (x) не существует.
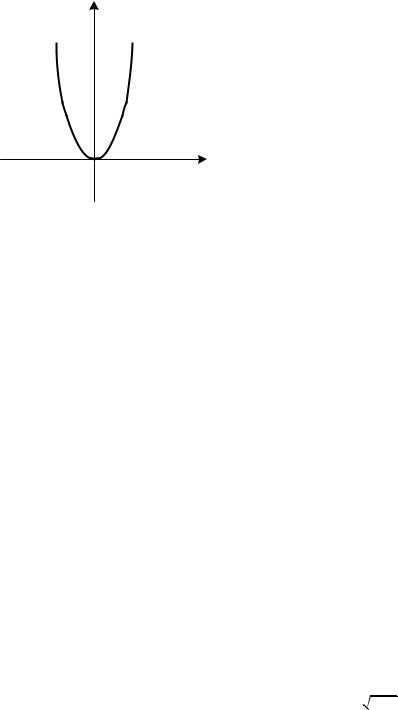
Условие теоремы 2.17 не является достаточным.
Покажем на примере функции y x4	(рис. 2.21).

Рисунок 2.21

При x 0 вторая производная y (x) 12x2 обращается в нуль, однако точки перегиба в точке x 0 нет.

Следовательно, точки, в которых вторая производная равна нулю либо не существует, подлежат дополнительному исследованию. Такие точки называют-

ся критическими точками второго рода функции y f (x) .

Теорема 2.18 (достаточное условие перегиба графика функции).

Пусть функция y f (x) определена в некоторой окрестности точки x0 ,

имеет вторую производную в указанной окрестности, кроме, может быть, точки x0 , и при переходе через точку вторая производная f (x0 ) меняет знак, тогда точка x0 , f (x0 ) на кривой является точкой перегиба.

Пример 2.34. Найти точки перегиба, интервалы выпуклости и вогнутости функции y x 3x 4 .

Решение. Функция определена на всей числовой оси. Найдем вторую производную:

3(x

4) x

x 12

y 3 x 4

3 3 (x 4)2

2(4x

12)

4 3

(x 4)2

12(x 4)

2(4x

12)

4x 24

откуда y

3 3 x 4

3 3 (x 4)4

9 3 (x 4)5

Найдем точки, в которых вторая производная равна нулю либо не существует:

1) y (x) 0,

4x 24 0

x 6;

2) y (x) не существует при

x 4 .

Итак, точки

x 4 и x 6 подлежат исследованию на перегиб. Определим знак второй производной в

каждом из образовавшихся интервалов и построим таблицу результатов исследования:

( , 4)

(4, 6)

(6, )

–

0 (перегиб)

63 2 (перегиб)

Таким образом, точки 4;0

и 6;6 3

являются точками перегиба.

Интервалы вогнутости:

, 4 и 6, . Интервал выпуклости:

(4, 6) .

2.11.4. Асимптоты графика функции

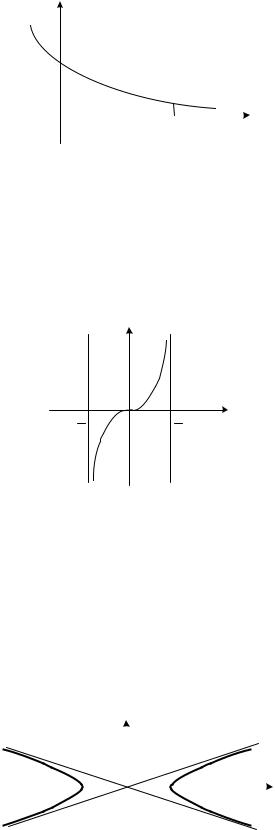
Определение. Прямая L называется асимптотой некоторой кривой y f (x) , если при удалении точки на бесконечность вдоль кривой расстояние

δ от точки до прямой L стремится к нулю (рис. 2.22).

y								δ
								δ	y f (x)
									y f (x)
								а
							т
						о
					т
				п
			м
		и
	с
	а
0									x
						Рисунок 2.22

		1	x
Пример 2.35. Построим график функции	y			(рис. 2.23).
Пример 2.35. Построим график функции	y			(рис. 2.23).
		3
y

y f (x)

Рисунок 2.23

Прямая y 0

является асимптотой графика функции y

Пример 2.36. Построим график функции

y tg x ,

(рис. 2.24).

π	0	π	x
	0		x
2		2

Рисунок 2.24

Вертикальные прямые x

и x

являются асимптотами графика функции

y tg x на рассмат-

риваемом интервале.

Пример 2.37. Построим график функции гиперболы

1 (рис. 2.25). Прямые

x являют-

ся асимптотами данной гиперболы.

Рисунок 2.25

По способу нахождения асимптоты различают вертикальные и наклон-

ные.

Замечание 1. Прямая x a является вертикальной асимптотой графика функции y f x , если хотя бы одно из предельных значений

lim

f x или

lim

f x

x a 0

равно или , то есть точка

x a является точкой бесконечного разрыва

функции y f x .

На рис. 2.24 прямые

являются вертикальными асимптотами гра-

фика функции y tg x на интервале

Замечание 2. Пусть

y kx b является наклонной асимптотой графика

функции y f x

(рис. 2.23, рис. 2.25). Параметры k и b вычисляются по сле-

дующим формулам

k lim

f x

b lim f x kx .

(2.18)

Аналогично определяются наклонные асимптоты при x .

Если хотя бы одно из предельных значений (2.18) не существует, то

наклонной асимптоты нет.

Пример 2.38. Найти асимптоты графика функции

2x2

x 2

Решение. Прямая x 2 является вертикальной асимптотой, так как

lim

2x2 3

, lim

2x2

x 2

x 2 0

Ищем наклонную асимптоту в виде y kx b . Воспользуемся формулами (2.18):

k lim

f x

lim

2x2 3

2 ;

b lim f

kx lim

2x2 3

lim

3 4x

4 .

x x

x x x 2

x 2

x x 2

Таким образом, прямая y 2x 4 является наклонной асимптотой.

Выполните практическое занятие 9.

Практическое занятие 9

Тема: Исследование функции с помощью производной

Пример 1. Найти интервалы монотонности и экстремумы функции:

у 2x3 3x2 .
Ответ:	Функция возрастает при x ( ,0)		(1, ) , функция убывает
при x (0,1),	уmax y(0) 0,	уmin y(1) 1.
			Помочь?

Подсказка 1.

Интервалы возрастания и убывания функции называются интервалами монотонности.

Если f (x) 0, x (a,b) , то функция возрастает на (a,b) .

Если f (x) 0, x (a,b) , то функция убывает на (a,b) .

Не понятно?

Подсказка 2.

Найдите для заданной функции критические точки первого рода и иссле-

дуйте изменение знака производной на полученных интервалах числовой пря-

мой.

Подробнее?

Подсказка 3.

Точки, в которых первая производная равна нулю либо не существует,

называются критическими точками первого рода:

y(x) 2x3 3x2 , y (x) 6x2 6x 6x(x 1) .

Критические точки первого рода: x1 0, x2 1.

Изобразите их на числовой прямой и определите знаки производной y (x)

на полученных интервалах.

Помочь?

Подсказка 4.


y (x)
	0	1	x

Знаки на интервалах расставлены в соответствие с методом интервалов.

Подробнее?

Подсказка 5.

Выберите на любом из полученных интервалов произвольную точку x0 и

вычислите в ней значение y x0 . Производная в выбранном интервале имеет тот же знак, что и число y x0 . Можно это проделать для каждого из интерва-

лов.

							Как?
Подсказка 6.
	2	2	6 2	12 0 , то		для x (1, ) . Аналогич-
Так как y (2) 6	2		6 2	12 0 , то	y (x) 0	для x (1, ) . Аналогич-
			для	x ( ,0)		0 для	x (0,1) . Следова-
но, получим, что y (x) 0			для	x ( ,0)	, и y (x)	0 для	x (0,1) . Следова-
тельно, функция возрастает при x ( ,0)					(1, ) и убывает при x (0,1) .
Теперь воспользуемся первым условием экстремума и найдем экстрему-
мы функции.
							Напомнить?
Подсказка 7.
Если производная				при переходе через точку			x0 меняет знак, а
Если производная			f (x)	при переходе через точку			x0 меняет знак, а

функция y f (x) определена в некоторой окрестности точки x0 , то в этой точ-

ке функция имеет экстремум.

Причем если производная меняет знак «+» на знак «–», то x0 – точка мак-

симума, а если знак «–» на знак «+», то x0 – точка минимума.

Дальше?

Подсказка 8.

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.02.2015146.94 Кб19Диплом_печать-1.doc
#
01.02.2015752.64 Кб33Диплом_печать-2.doc
#
20.03.20162.53 Mб50Дипломная работа.rtf
#
02.02.2015428.09 Кб41Дисципліни терапевтичного профілю.rtf
#
02.02.2015222.67 Кб7Дисципліни хірургічного профілю.rtf
#
07.03.20151.88 Mб48Дифференциальное исчисление_эл.учебник.pdf
#
02.02.201587.05 Кб7дкп.docx
#
21.11.201943.79 Кб2дкр-право.docx
#
20.08.2019135.68 Кб21Для Магистров Сем 3 .doc
#
20.08.2019142.85 Кб2Для магистров сем 1 .doc
#
02.02.201513.25 Mб496Для первокурсеника.pdf