Метод половинного деления

Пусть f(x) – непрерывная функция на [a;b], .

1. Находим середину отрезка .

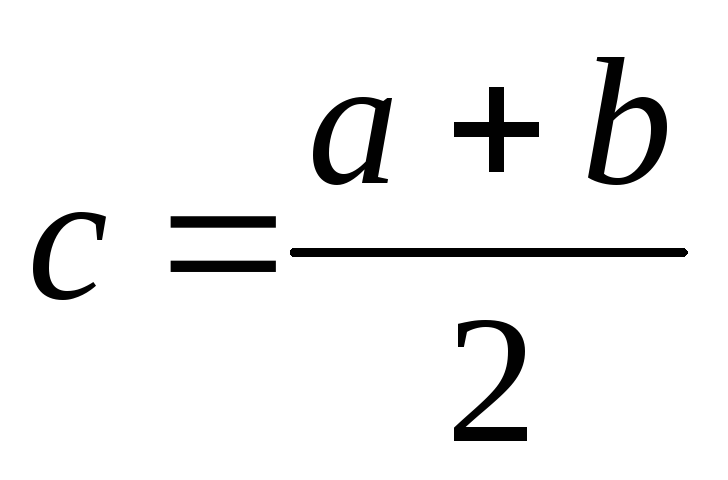2. Вычисляем .

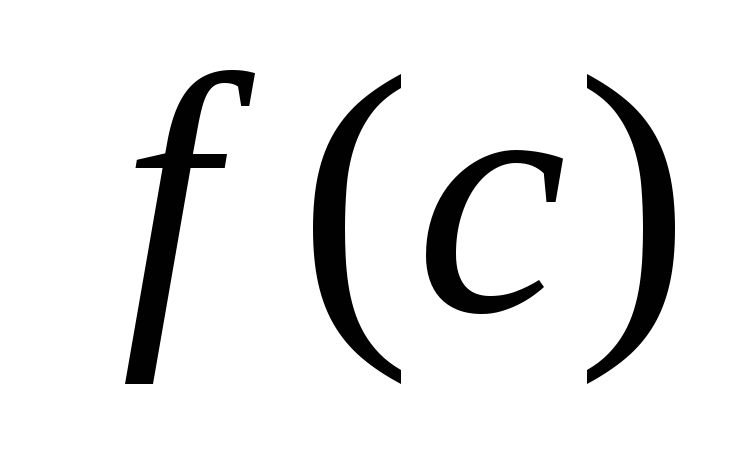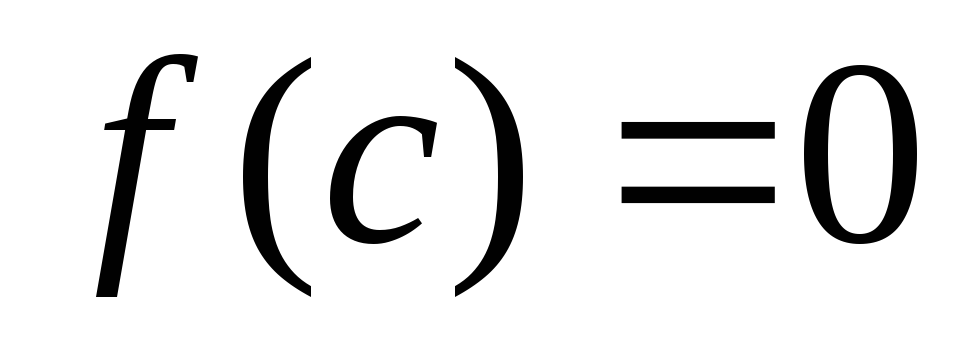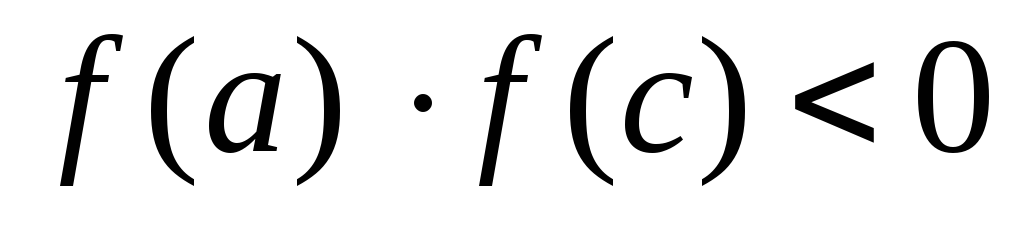3. Если , то полагаем, что корень равенc и заканчиваем вычисления. Если , то полагаем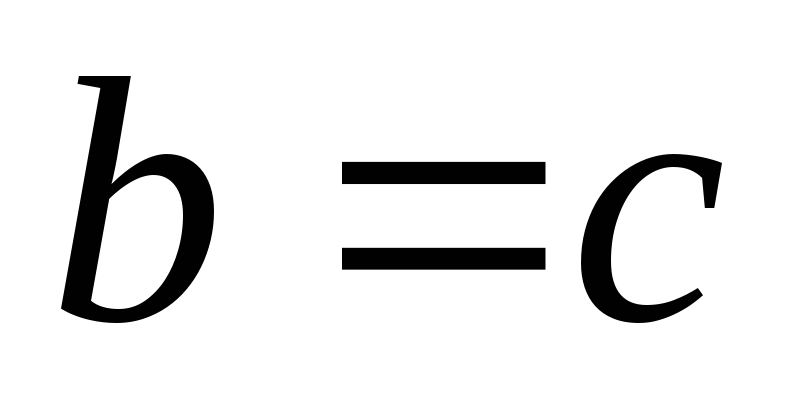, иначе.

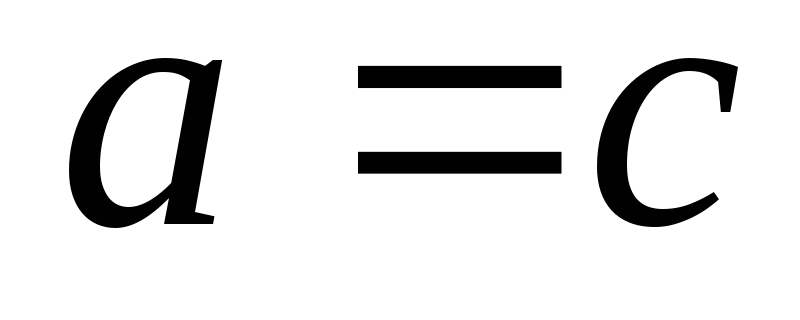4. Если 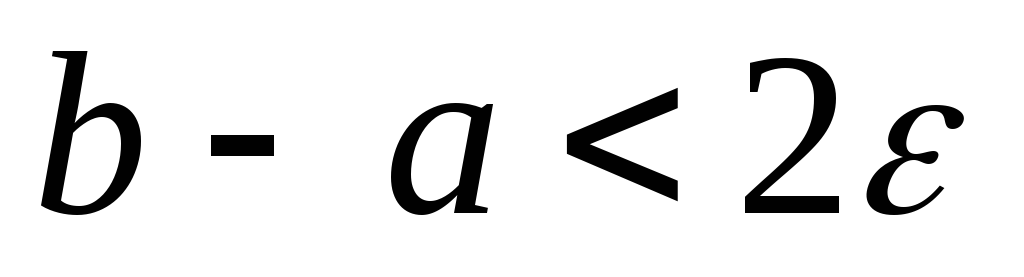, то в качестве корня берем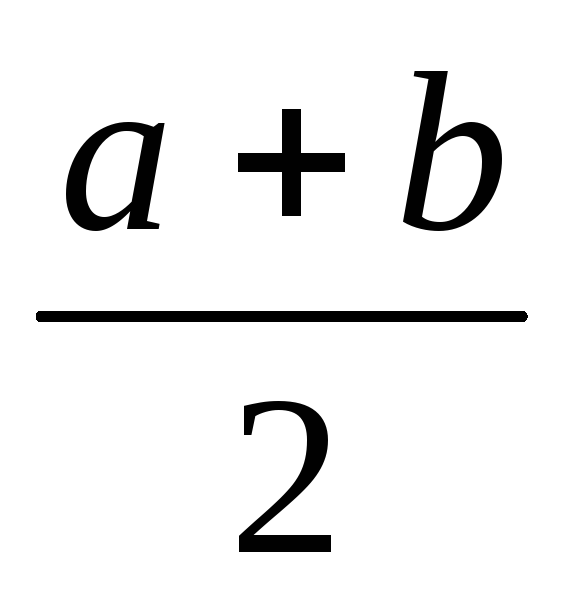и заканчиваем вычисления, в противном случае переходим к пункту 1.

Метод Ньютона (метод касательных)

Пусть f(x) – дважды непрерывно дифференцируемая функция на отрезке [a;b], ,ине меняют знак на [a;b].

Обозначим через тот конец отрезка, где знакиисовпадают. Последовательные приближения к точному корнюc находим по формуле

для .

Тогда является точным корнем уравнения (1).

Вычислительный процесс обычно останавливают, когда оказывается меньше заданной точностиε. Однако это условие не может строго гарантировать, что заданная точность достигнута. Для полной гарантии можно выполнить проверку точности, как было указано в начале раздела. Если точность не достигнута, то нужно повторить итерации еще несколько раз.

Метод секущих

Пусть есть какое-то начальное приближение . Получим еще одну точку по формуле, гдеh – небольшое число. Будем считать, что мы выполнили несколько шагов метода, и к данному моменту у нас есть два последовательных приближения ик точному корню (на начальном этапе – этои). Тогда следующее приближение находим по формуле

,

Процесс останавливается по такому же критерию, как и в методе Ньютона.

Метод итераций

В методе итераций исходное уравнение (1) преобразуется в равносильное уравнение . Выбирается начальное приближение. Каждое следующее приближение получается по формуле,Процесс останавливается по тому же критерию, что и в методе Ньютона. Метод будет сходиться, т.е. пределравен точному значению корня, если в окрестности корня выполнено неравенствои начальное приближение находится достаточно близко к корню.

Преимущества и недостатки методов

Метод половинного деления требует отделения корня, и для достижения высокой точности приходится вычислять функцию много раз. Достижение заданной точности в этом методе гарантировано.

Метод Ньютона обладает очень быстрой сходимостью (квадратичная сходимость), т.е.

,

где c – точное значение корня; M – некоторая константа, зависящая от функции. Грубо говоря, начиная с некоторой итерации, число верных знаков после запятой станет удваиваться на каждой итерации.

Для гарантии сходимости метода Ньютона требуется выполнение довольно многих условий. Вообще говоря, начать вычисления по методу Ньютона можно и без проверки этих условий, но тогда сходимость может не наблюдаться.

Метод секущих обеспечивает для гладких функций скорость сходимости, близкую к скорости сходимости метода Ньютона. Он не требует вычисления производной функции. Если начальная точка взята далеко от корня, то сходимость может отсутствовать.

Метод итераций дает скорость сходимости значительно меньшую, чем метод Ньютона. При наличии сходимости действует оценка , где– числа,,;c –точное значение корня. Величины M, q зависят от функции и не зависят от номера итерации. Если же близок к 1, тоq тоже близко к 1 и сходимость метода будет медленной. Счет по методу итераций можно начать без проверки условий на и. В этом случае процесс может оказаться расходящимся, и тогда ответ не будет получен.

Существует много методов нахождения корней нелинейного уравнения, отличных от перечисленных. В MATHCAD функция root в формате использует метод секущих, а если он не приводит к желаемым результатам, то – метод Мюллера. В последнем, в отличие от метода секущих, на каждом шаге берутся две дополнительные точки, график функции заменяется параболой, проходящей через три точки, и за следующее приближение берется точка пересечения параболы с осьюOx. В функции root в формате root(f(x),x,a,b) используются методы Риддера и Брента. Для нахождения корней многочлена в MATHCAD используется метод Лагерра.