
- •Оглавление предисловие
- •Основные понятия и вычислительные методы (теоретическая часть)
- •Метод Гаусса
- •Метод lu-разложения
- •Обращение матрицы и вычисление определителя
- •Число обусловленности матрицы (системы уравнений)
- •Вычислительные методы для решения нелинейных уравнений
- •Метод половинного деления
- •Метод Ньютона (метод касательных)
- •Метод секущих
- •Метод итераций
- •Преимущества и недостатки методов
- •Методы решения систем нелинейных уравнений
- •Метод Ньютона для систем уравнений
- •Метод итераций для систем уравнений
- •Некоторые сведения о полиномах и их корнях
- •Полиномиальные уравнения
- •Вычисление интегралов
- •Дифференциальные уравнения (численные методы)
- •Жесткие системы дифференциальных уравнений
- •Аналитическое решение систем линейных дифференциальных уравнений с постоянными коэффициентами
- •Нахождение экстремумов функции нескольких переменных
- •Метод покоординатного спуска
- •Симплекс-метод
- •Метод наискорейшего спуска
- •Метод Ньютона
- •Преобразования Фурье и Лапласа
- •Применение системы mathcad для решения вычислительных задач (практическая часть)
- •Исправления
- •Продолжение простейших вычислений
- •Точность
- •Символьные вычисления
- •Переменные
- •Функции пользователя
- •Операции математического анализа
- •Построение графиков функций одного переменного
- •Задания для самостоятельной работы
- •Матрицы
- •Векторы
- •Системы линейных уравнений
- •Число обусловленности матрицы
- •Собственные числа и собственные векторы матрицы
- •Графики функций двух переменных
- •Задания для самостоятельной работы
- •Нахождение корней нелинейного уравнения
- •Решение систем нелинейных уравнений
- •Корни многочлена
- •Наибольший общий делитель двух многочленов
- •Кратные корни
- •Результант
- •Задания для самостоятельной работы
- •Полиномиальные уравнения
- •Вычисление определенных интегралов
- •Решение дифференциальных уравнений
- •Задания для самостоятельной работы
- •Системы дифференциальных уравнений
- •Решение жестких систем дифференциальных уравнений
- •Решение линейных систем дифференциальных уравнений с постоянными коэффициентами
- •Задания для самостоятельной работы
- •Нахождение экстремумов функции
- •Экстремумы функции многих переменных
- •Преобразования Фурье и Лапласа
- •Дискретное преобразование Фурье
- •Задания для самостоятельной работы
Задания для самостоятельной работы
Решите полиномиальное уравнение
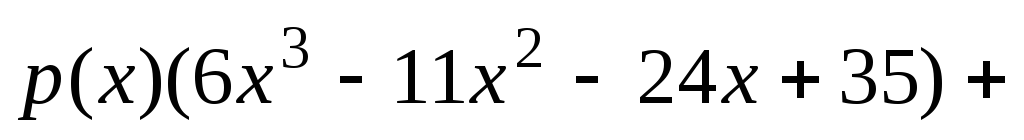
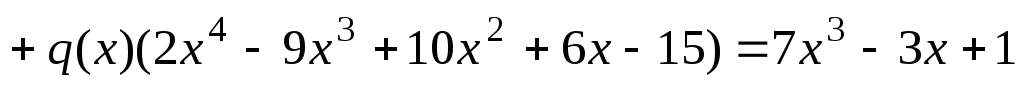 .
.Решите полиномиальное уравнение
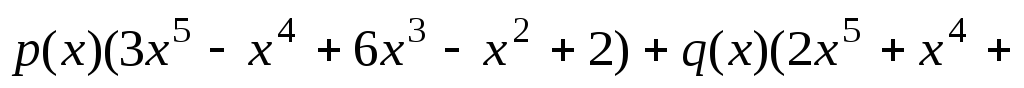
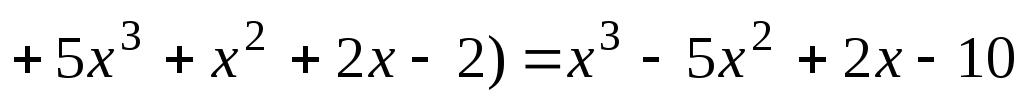 .
.Вычислите интеграл по отрезку [−2; 3] от функции
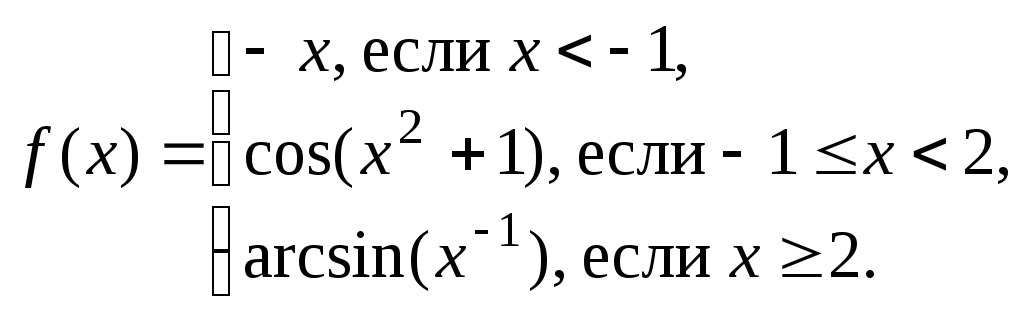
Вычислите интеграл
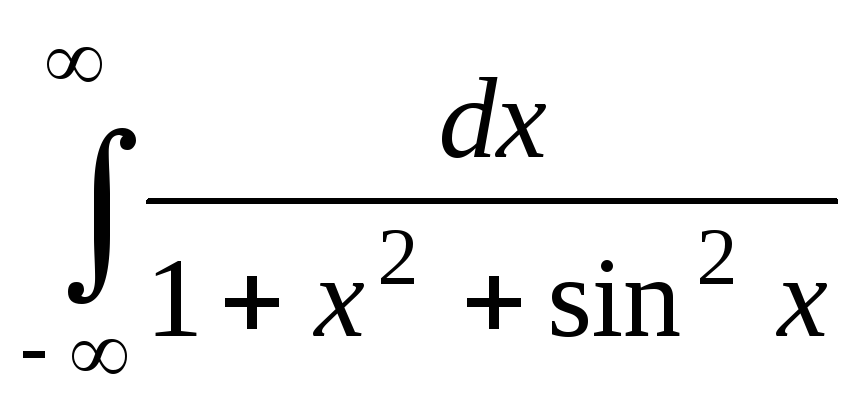 .
.Найдите два решения дифференциального уравнения
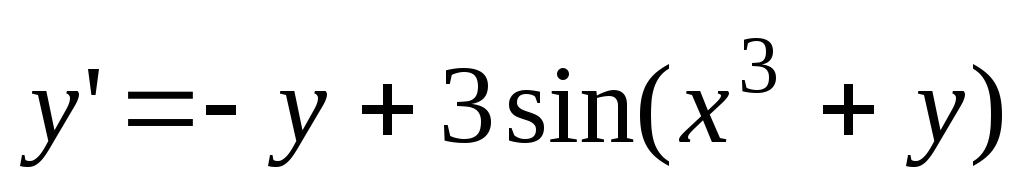 на отрезке [1; 5] с начальными условиями
соответственно
на отрезке [1; 5] с начальными условиями
соответственно ,
,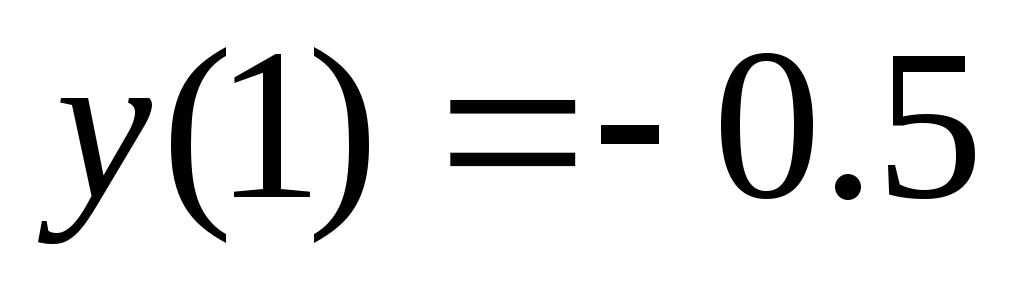 .
Проконтролируйте достижение точности
0.001. Нарисуйте их графики (на одном
чертеже). Определите значения этих
решений в точкеx = 4.85.
.
Проконтролируйте достижение точности
0.001. Нарисуйте их графики (на одном
чертеже). Определите значения этих
решений в точкеx = 4.85.Найдите решение дифференциального уравнения
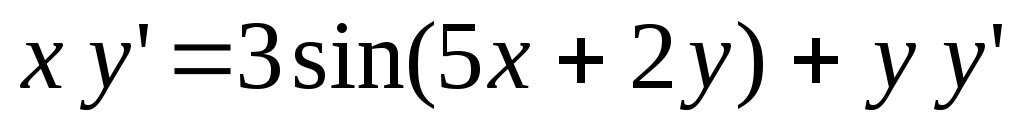 на отрезке [2; 4] с начальным условием
на отрезке [2; 4] с начальным условием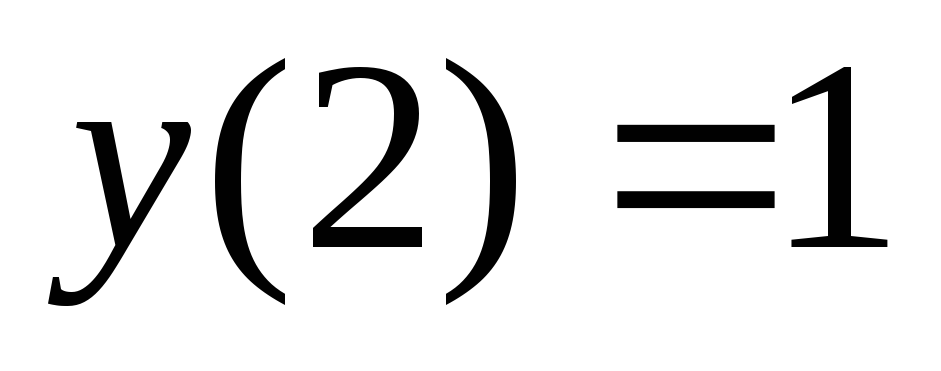 .
Нарисуйте график этого решения. Найдите
значение этого решения в точкеx = 3.75
с точностью
.
Нарисуйте график этого решения. Найдите
значение этого решения в точкеx = 3.75
с точностью
 .
.
Лабораторная работа №5
Системы дифференциальных уравнений
Эту тему рассмотрим на конкретных примерах. Использование функций для решения систем практически ничем не отличается от случая одного дифференциального уравнения.
Пусть требуется решить систему дифференциальных уравнений
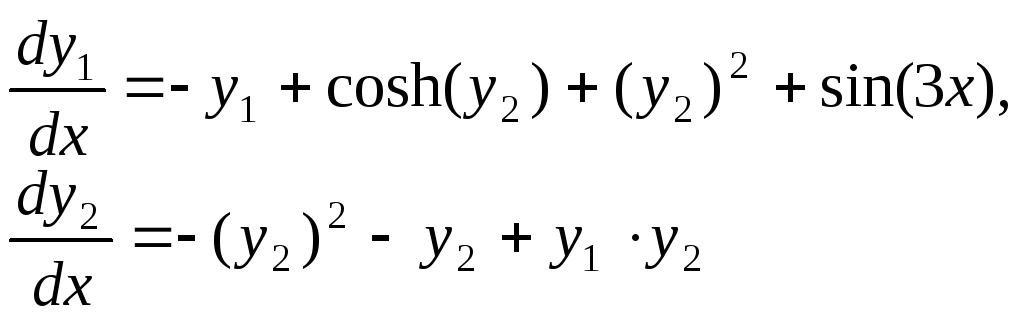
с начальными условиями:
начальными условиями:![]() ,
,![]() при
при![]() .
Решать систему будем на отрезке [0; 4].
.
Решать систему будем на отрезке [0; 4].
Создадим
вектор правых частей системы уравнений.
При этом нужно учитывать, что
![]() и
и![]() являются компонентами вектораy.
В МС нумерация компонент по умолчанию
начинается с нуля. Следовательно, или
нужно изменить индексы у неизвестных
функций, или установить нумерацию
компонент с единицы. Далее считаем, что
нумерация компонент начинается с
единицы. Создадим вектор начальных
условий
являются компонентами вектораy.
В МС нумерация компонент по умолчанию
начинается с нуля. Следовательно, или
нужно изменить индексы у неизвестных
функций, или установить нумерацию
компонент с единицы. Далее считаем, что
нумерация компонент начинается с
единицы. Создадим вектор начальных
условий
![]() .
Создадим также вектор-функцию правой
части системы дифференциальных уравнений:
.
Создадим также вектор-функцию правой
части системы дифференциальных уравнений:
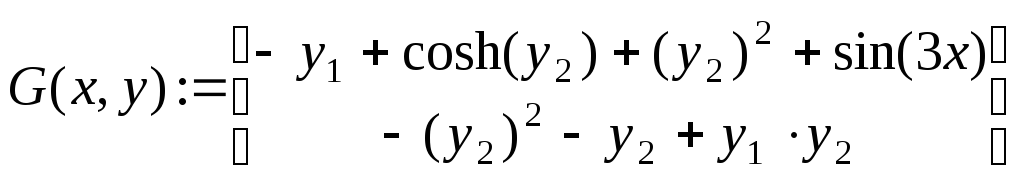 .
.
Применим функцию Rkadapt:
![]() .
.
Посмотрим
матрицу Y,
которая приведена на рис. 36. Видим, что
она содержит три столбца, первый, как и
раньше, дает сетку узлов интегрирования,
второй – значения первой компоненты
решения
![]() ,
третий – второй компоненты решения
,
третий – второй компоненты решения![]() .
Графики этих функций приведены на рис.
37.
.
Графики этих функций приведены на рис.
37.
Стоит
попробовать найти решение при начальных
условиях
![]() ,
,![]() при
при![]() .
Попытайтесь проанализировать результат.
.
Попытайтесь проанализировать результат.
Е сли
правая часть системы дифференциальных
уравнений
сли
правая часть системы дифференциальных
уравнений![]() не содержит независимого переменногоx,
то система называется автономной. Такие
системы обладают некоторыми специфическими
свойствами. Для них, в частности, можно
рисовать так называемые фазовые кривые,
то есть проекции интегральных кривых
на пространство переменных y.
Эти проекции не перекрывают друг друга
и являются траекториями движения точки,
закон движения которой задан системой
дифференциальных уравнений.
не содержит независимого переменногоx,
то система называется автономной. Такие
системы обладают некоторыми специфическими
свойствами. Для них, в частности, можно
рисовать так называемые фазовые кривые,
то есть проекции интегральных кривых
на пространство переменных y.
Эти проекции не перекрывают друг друга
и являются траекториями движения точки,
закон движения которой задан системой
дифференциальных уравнений.
Рассмотрим автономную систему
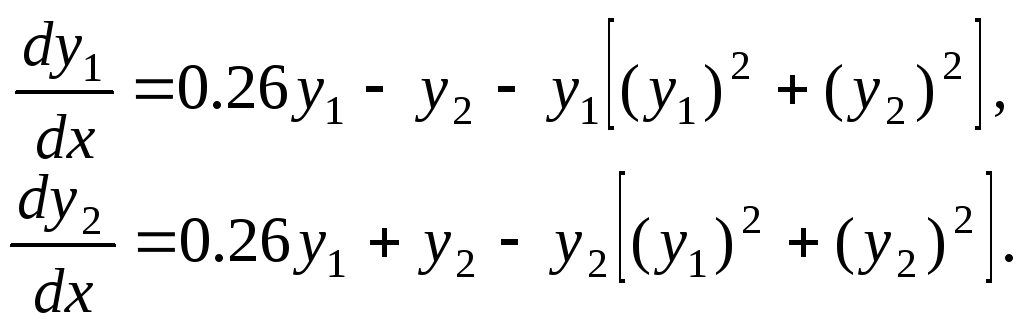
Найдем
ее решение с начальными условиями
![]() ,
,![]() при
при![]() на отрезке [0; 20].
Для этого сформируем вектор правых
частей
на отрезке [0; 20].
Для этого сформируем вектор правых
частей
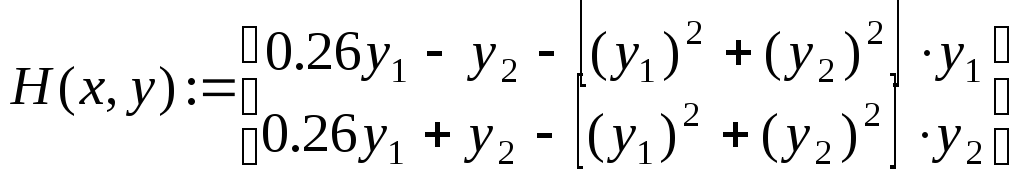 .
.
Здесь
в описании функции аргумент x
нужно указывать обязательно,
хотя в правой части в действительности
он отсутствует. Сформируем вектор
начальных условий
![]() .
.
Найдем матрицу значений решения этой системы
![]() .
Изображение фазовой кривой
.
Изображение фазовой кривой

(фазовый портрет решения) приведено на рис. 38, графики компонент решения – на рис. 39.
Для решения систем дифференциальных уравнений можно также применять функцию Оdesolve. В этом случае у нее появляется еще один обязательный аргумент. Уравнения, входящие в систему, могут иметь произвольный порядок. Важно, чтобы производные старшего порядка входили в систему линейно. Каждая неизвестная функция системы должна иметь свое имя. Нельзя их создавать, как компоненты вектора! В записи уравнений системы у каждой неизвестной функции и ее производных обязательно указывать аргумент. Знак равенства берется с панели Boolean.
Для использования функции Оdesolve создается вычислительный блок. Он начинается директивой given. Далее записываются уравнения системы и начальные условия. Затем записывается оператор присвоения с функцией Оdesolve. В левой части этого оператора записывается матрица-столбец, элементами которой служат имена функций, которые составляют решение системы. Аргумент в этих функциях не указывается. Ставится знак присвоения := и пишется функция Оdesolve. Ее первый аргумент – это матрица-столбец с именами неизвестных функций системы без указания их аргумента. Второй аргумент функции Оdesolve – имя независимой переменной. Третий аргумент – конечная точка отрезка интегрирования. Четвертый аргумент – число узлов интегрирования. Четвертый аргумент является необязательным. По умолчанию в МС14 он равен 1000. Его стоит указывать, если есть необходимость проконтролировать точность решения системы уравнений. Переменная TOL не влияет на точность.
Решим
с использованием функции Оdesolve
систему уравнений
![]() на отрезке [0; 2] с начальными условиями:
на отрезке [0; 2] с начальными условиями:![]() ,
,![]() ,
,![]() ,
,![]() .
.
Обратим
внимание, что в записи этой системы
точки над буквами заменяют символ ‘,
т.е. символ дифференцирования. Такое
обозначение обычно используется, если
независимым аргументом служит t
(в физике t
– обозначение времени). В рассматриваемой
системе независимым аргументом служит
t.
При записи уравнений в МС в качестве
символа производной можно использовать
только ‘ или
![]() ,
последний берется с панелиCalculus.
,
последний берется с панелиCalculus.
Создаем вычислительный блок (знак = с панели Boolean):
given
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Теперь
мы можем найти значения неизвестных
функций в любой точке отрезка [0; 2],
например, при
![]() :
:
![]()
![]() .
.
Если
рассмотренную систему уравнений
превратить в систему из четырех уравнений
первого порядка, то ее решение с помощью
функции Rkadapt
даст при
![]() результат,
отличающийся лишь в четвертом знаке
после запятой. Это достаточно хорошая
точность. Можно построить графики
решений (рис.40).
результат,
отличающийся лишь в четвертом знаке
после запятой. Это достаточно хорошая
точность. Можно построить графики
решений (рис.40).

Функцию Оdesolve разумно использовать, когда число уравнений в системе невелико. В противном случае запись столбца с именами неизвестных функций будет затруднительна. Преимуществом этой функции служит то, что она автоматически определяет является ли система жесткой или нет, и выбирает соответствующий метод численного решения дифференциальных уравнений.
