
m_ukazanija__05
.doc
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Методические указания к выполнению расчётного задания
для студентов заочного отделения всех специальностей
Москва 2007
Цель настоящих методических указаний – помочь студентам в приобретении навыков нахождения неопределённых интегралов различных типов.
Типовой расчёт по теме «Интегральное исчисление функции одной переменной » для студентов заочного отделения всех специальностей содержит 25 вариантов, в каждом варианте 20 примеров. Первые 14 примеров предполагают использование основных методов интегрирования. 15*, 16*, 17* – примеры повышенной трудности. Интегралы из примеров 18, 19, 20 находятся с помощью справочника: Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1986. Возможно использование других справочников.
Далее приведено решение примерного варианта типового расчёта с краткими методическими указаниями.
Основные понятия.
Функция
![]() называется первообразной для функции
называется первообразной для функции
![]() ,
если
,
если
![]() .
.
Совокупность всех
первообразных для функции
![]() называется неопределённым интегралом
от этой функции и обозначается
называется неопределённым интегралом
от этой функции и обозначается
![]() .
Если
.
Если
![]() – какая- либо первообразная для
– какая- либо первообразная для
![]() ,
то
,
то
![]() .
.
Нахождение неопределённых интегралов называется интегрированием.
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
![]() 12.
12.![]()
2.![]() 13.
13.![]()
3.![]() 14.
14.![]()
4.![]() 15.
15.![]()
5.![]() 16.
16.![]()
6.
![]() 17.
17.![]() 7.
7.
![]() 18.
18.![]()
8.
![]() 19.
19.![]()
9.
![]() 20.
20.![]() 10.
10.
![]() 21.
21.![]()
11.![]() 22.
22.![]()
Основные правила интегрирования
-
Интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых:
![]()
-
Постоянный множитель можно выносить за знак интеграла:
![]()
-
Вид формул интегрирования не изменится, если независимую переменную x заменить любой дифференцируемой функцией от x, т. е. если
 и
и
 – дифференцируемая функция, то
– дифференцируемая функция, то
 .
. -
Если
 - дифференцируемая функция, то
- дифференцируемая функция, то
 .
При применении этого правила можно
использовать таблицу основных
дифференциалов.
.
При применении этого правила можно
использовать таблицу основных
дифференциалов.
Таблица основных дифференциалов.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
,
4)
![]() ,
5)
,
5)
![]() ,
6)
,
6)
![]() ,
,
7)
![]() ,
8)
,
8)
![]() ,
,
9)
![]() ,
10)
,
10)
![]() ,
,
11)
![]() ,
12)
,
12)
![]() ,
,
13)
![]() ,
14)
,
14)
![]() ,
,
15)
![]() ,
,
16)
![]() ,
,
17)
![]() .
.
Решение примерного варианта типового расчёта.
Пример 1. Воспользуемся следующим свойством неопределённого интеграла:
![]()
и таблицей основных интегралов.
а)
![]() ,
( интеграл №3 ),
,
( интеграл №3 ),
б)
![]() (
интеграл №5 ),
(
интеграл №5 ),
в)
![]() (
интеграл №9 ).
(
интеграл №9 ).
Пример 2.
Воспользуемся алгебраическим тождеством:
![]() и правилами интегрирования 1 и 2.
и правилами интегрирования 1 и 2.
а)
![]()
![]()
б)


![]()

Пример 3 и 4. Решаем методом подведения функции под знак дифференциала.
а)![]()
![]() ;
;
б)![]() ;
;
в)

![]() .
.
Пример 5. При интегрировании чётных степеней синуса или косинуса применяются формулы понижения степени:
![]() .
.
а)
![]()
![]() ;
;
б)
![]()
![]()
![]()
![]() .
.
Пример 6. При интегрировании нечётных степеней синуса или косинуса поступают следующим образом: от нечётной степени функции sinkx или coskx отделить сомножитель в первой степени, подвести его под знак дифференциала:
![]()
![]() ,
,
а оставшуюся чётную
степень функции sinkx
или coskx
преобразовать, используя основное
тригонометрическое тождество:
![]() .
.
а)
![]()
![]()
![]()
![]() .
.
б)
![]()
![]()
![]() .
.
Интегралы в
примерах 7, 8 и 9 вычисляются методом
интегрирования по частям по формуле:
![]() ,
где
,
где
![]() .
При интегрировании этим методом важно
правильно разбить подынтегральное
выражение на две части: u
и dv.
Если под знаком интеграла стоит
произведение многочлена на одну из
функций: синус, косинус или показательную
функцию, то через u
обозначают
многочлен, а через dv
– всё остальное.
.
При интегрировании этим методом важно
правильно разбить подынтегральное
выражение на две части: u
и dv.
Если под знаком интеграла стоит
произведение многочлена на одну из
функций: синус, косинус или показательную
функцию, то через u
обозначают
многочлен, а через dv
– всё остальное.
![]()
Если под знаком
интеграла содержатся логарифмическая
или обратные тригонометрические
функции: арксинус, арккосинус, арктангенс,
арккотангенс, то их обозначают через
u,
а через dv
– всё остальное.

Пример 7.
а)


б)


Пример 8.

![]()
![]()
Пример 9.


Примеры 10 и 11 содержат квадратный трёхчлен в знаменателе. Поэтому, сначала из квадратного трёхчлена выделяется полный квадрат по формуле:
![]()
а затем знаменатель
упрощается с помощью замены переменной:
![]() .
.
Пример 10.
а)
![]() .
.
В знаменателе –
квадратный трёхчлен
![]() .
Выделим полный квадрат:
.
Выделим полный квадрат:
![]()

б)
![]() .
.
В знаменателе –
квадратный трёхчлен
![]() .
Выделим полный квадрат:
.
Выделим полный квадрат:


Пример 11.
а)
![]() .
.
В знаменателе –
квадратный трёхчлен
![]() .
Выделим полный квадрат:
.
Выделим полный квадрат:
![]()

б)
![]() .
.
В знаменателе –
квадратный трёхчлен
![]() .
Выделим полный квадрат:
.
Выделим полный квадрат:


Пример 12 содержит под знаком интеграла дробно – рациональную функцию. Если под знаком интеграла стоит правильная рациональная дробь (степень многочлена в числителе меньше степени многочлена в знаменателе), то её можно представить в виде суммы простейших дробей:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Пример 12.
а)
![]() .
.
Разложим знаменатель на множители:
![]()
Квадратный трёхчлен можно разложить на множители
![]() ,
,
где
![]() и
и
![]() – корни соответствующего квадратного
уравнения
– корни соответствующего квадратного
уравнения
![]()
![]()

Представим правильную рациональную дробь в виде суммы простейших дробей:
![]() .
.
Для нахождения коэффициентов А, В и С приведём дроби, стоящие в правой части к общему знаменателю
![]() .
.
Приравняем числители дробей:
![]() .
.
Так как полученные многочлены должны быть тождественно равны, то их значения должны быть равны при любых значениях x. Подставим значения x, равные корням знаменателя, в последнее равенство.

Окончательно
имеем:

б)
![]()
Представим правильную рациональную дробь в виде суммы простейших дробей:
![]() .
.
Для нахождения коэффициентов А, В и С приведём дроби, стоящие в правой части к общему знаменателю
![]()
Приравняем числители дробей:
![]() .
.
Раскроем скобки и приведём подобные в правой части равенства:
![]()
Приравняем коэффициенты при одинаковых степенях x в левой и правой частях равенства:
при
![]()
при
![]()
при
![]()
Решим систему трёх уравнений с тремя неизвестными:

Окончательно имеем:
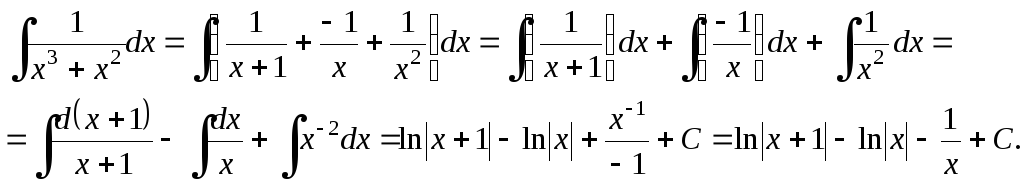
в)
![]()
Представим правильную рациональную дробь в виде суммы простейших дробей:
![]() .
.
Для нахождения коэффициентов А, В и С приведём дроби, стоящие в правой части к общему знаменателю
![]() .
.
Приравняем числители дробей:
![]() .
.
Раскроем скобки и приведём подобные в правой части равенства:
![]()
Приравняем коэффициенты при одинаковых степенях x в левой и правой частях равенства:
при
![]()
при
![]()
при
![]()
Решим систему трёх уравнений с тремя неизвестными:

Окончательно имеем:

В примерах 13 и 14 под знаком интеграла содержатся корни различных степеней из x или из линейного выражения ax+b. В этом случае применяется подстановка:
![]() или
или
![]() ,
где n
– наименьшее общее кратное всех степеней
корней из x
или из линейного выражения ax+b,
встречающихся в подынтегральном
выражении.
,
где n
– наименьшее общее кратное всех степеней
корней из x
или из линейного выражения ax+b,
встречающихся в подынтегральном
выражении.
Пример 13.

Под знаком интеграла стоит неправильная рациональная дробь (степень многочлена в числителе больше степени многочлена в знаменателе), поэтому сначала выделяем целую часть этой дроби, разделив числитель на знаменатель «уголком».
 Тогда
Тогда
![]() .
.
Окончательно имеем:

Пример 14.

Под знаком интеграла стоит неправильная рациональная дробь (степень многочлена в числителе равна степени многочлена в знаменателе), поэтому сначала выделяем целую часть этой дроби. Для этого вычтем и добавим 1 в числителе и разложим на два слагаемых.
![]()
Окончательно имеем:

Пример 15*.

![]() .
.
Интеграл
![]() вычислим отдельно (интегрирование по
частям).
вычислим отдельно (интегрирование по
частям).
![]()

![]() .
.
Интегрируем ещё раз по частям, не меняя обозначений.
![]()

![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
Перенесём
![]() в правую часть равенства с противоположным
знаком.
в правую часть равенства с противоположным
знаком.
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
В результате получим:
![]()
![]()
![]() .
.
Пример 16*.
![]() .
.
В знаменателе –
квадратный трёхчлен
![]() .
Выделим полный квадрат:
.
Выделим полный квадрат:


Пример 17*.
![]()

Применяем универсальную тригонометрическую подстановку:
 .
Тогда
.
Тогда
![]()
Обозначим:
![]()
![]()

При вычислении интегралов №18, 19 и 20 следует пользоваться справочником: Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1986 (1998 и др.)(*). Возможно использование других справочников. Вначале следует внимательно ознакомиться с содержанием и структурой раздела « Таблица неопределённых интегралов»: из каких частей состоит раздел и какие вводятся обозначения.
Пример 18.
![]()
В таблице
неопределённых интегралов справочника
(*) в разделе «Интегралы от иррациональных
функций. Интегралы, содержащие
![]() »
находим формулу №245:
»
находим формулу №245:
![]() ,
где
,
где
![]() ,
,
![]() вычисляется по формуле №241.
вычисляется по формуле №241.
В нашем примере:
![]()
По формуле №245 имеем:
![]() ,
,
а в формуле №241
значению
![]() соответствуют три первых строки. Так
как
соответствуют три первых строки. Так
как
![]() ,
то выбираем из двух первых. При этом
первая – при
,
то выбираем из двух первых. При этом
первая – при
![]() любого знака, а вторая – только для
любого знака, а вторая – только для
![]() .
Выбираем первую.
.
Выбираем первую.
![]()
Окончательно имеем:

Пример 19.

В таблице
неопределённых интегралов справочника
(*) в разделе «Интегралы от иррациональных
функций. Интегралы, содержащие
![]() »
находим формулу №162:
»
находим формулу №162:
![]() ,
где
,
где
![]() .
В данном интеграле
.
В данном интеграле
![]()
![]()
Окончательно имеем:

![]()
Пример 20.
![]() .
.
В таблице неопределённых интегралов справочника (*) в разделе «Интегралы от тригонометрических функций. Интегралы, содержащие косинус» находим формулу №317:
![]() ,
n
– целое,
,
n
– целое,
![]()
Эту формулу применяем несколько раз, пока не получим интеграл вида:
![]() или
или
![]() .
.

