
Несобственные интегралы
.docxМинистерство образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Курсовая работа по теме
«Несобственные интегралы.
Интегрирование несобственных интегралов по частям.
Вычисление интеграла
 .»
.»
Выполнил: Шаповалов Николай Сергеевич
Принял: Мясников Алексей Георгиевич
.
Москва 2013
Несобственные интегралы.
Интегрирование несобственных интегралов по частям.
Вычисление интеграла
 .
.
.Несобственные интегралы. Интегралы с бесконечными пределами.
Говоря об определенных интегралах ,мы до сих подразумевали, что интервал интегрирования конечен и замкнут и подынтегральная функция на нем непрерывна. Однако довольно часто возникает необходимость распространить определение определенного интеграла на случай бесконечного интервала интегрирования или на случай неограниченной подынтегральной функции.
Пусть
функция
 непрерывна в бесконечном интервале
[a,+∞).
Тогда мы можем вычислить интеграл от
функции
непрерывна в бесконечном интервале
[a,+∞).
Тогда мы можем вычислить интеграл от
функции взятый по любому интервалу
взятый по любому интервалу


Заставим
 неограниченно возрастать. Имеются две
возможности: или
неограниченно возрастать. Имеются две
возможности: или
 при
при
 имеет предел, или
имеет предел, или
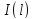 предела не имеет. Логическим выводом
из этого утверждения является следующее
определение:
предела не имеет. Логическим выводом
из этого утверждения является следующее
определение:
Определение.
Сходящимся
несобственным интегралом
 от функции
от функции
 в интервале
в интервале называется предел интеграла
называется предел интеграла при
при ,
если этот предел существует. Записывается
это так:
,
если этот предел существует. Записывается
это так:

Коротко
говорят, что интеграл сходится.
Если этот
предел не существует, то равенство (1)
теряет смысл и несобственный интеграл,
стоящий слева, называется расходящимся.
При этом
 или стремится к бесконечности, или
вообще не стремится ни к какому пределу.
Если первообразная функция
или стремится к бесконечности, или
вообще не стремится ни к какому пределу.
Если первообразная функция
 для подынтегральной функции
для подынтегральной функции
 известна, то легко установить сходится
несобственный интеграл или нет. С помощью
формулы Ньютона-Лейбница получаем:
известна, то легко установить сходится
несобственный интеграл или нет. С помощью
формулы Ньютона-Лейбница получаем:

Если
 существует, в этом случае интеграл
сходится. Если этот предел не существует,
то интеграл расходится.
существует, в этом случае интеграл
сходится. Если этот предел не существует,
то интеграл расходится.
Примеры.
1)
 Следовательно, несобственный интеграл
Следовательно, несобственный интеграл
 сходится и равен 1.
сходится и равен 1.
2)
 Интеграл расходится, так как первообразная
Интеграл расходится, так как первообразная
 при
при
 стремится к бесконечности.
стремится к бесконечности.
3)
 расходится, так как величина
расходится, так как величина
 не стремится к пределу при
не стремится к пределу при
 (а колеблется от -1 до 1)
(а колеблется от -1 до 1)
Аналогично
определяется несобственный интеграл
и в интервале


Где
 -предел
первообразной
-предел
первообразной
 при
при
 ,
если он существует. Если функция
определена и непрерывна на всей числовой
оси, то можно рассматривать и несобственный
интеграл в интервале
,
если он существует. Если функция
определена и непрерывна на всей числовой
оси, то можно рассматривать и несобственный
интеграл в интервале
 .
По определению
.
По определению

Если
оба интеграла в правой части сходятся
,то интеграл
 называется сходящимся. Если хотя бы
один из интегралов справа расходится,
то равенство теряет смысл и интеграл
слева называется расходящимся.
называется сходящимся. Если хотя бы
один из интегралов справа расходится,
то равенство теряет смысл и интеграл
слева называется расходящимся.
Если
первообразная
 известна, то
известна, то
 ,
,
Где
под символами

 понимают
пределы (если они существуют),к которым
стремится
понимают
пределы (если они существуют),к которым
стремится
 соответственно
при
соответственно
при
 и
и
 Если хотя бы
один из этих пределов не существуют, то
несобственный интеграл расходится.
Если хотя бы
один из этих пределов не существуют, то
несобственный интеграл расходится.
Примеры
4)

5)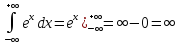
6) Здесь
Здесь

 равны бесконечности, интеграл расходятся.
равны бесконечности, интеграл расходятся.
Заметим,
что несобственные интегралы без всяких
изменений переносят простейшие свойства
определенного интеграла. Сходящимся
несобственным интегралам можно придать
определенный геометрический смысл.
Пусть, например, график функции
 ограничивает трапецию с бесконечным
основание(рис. 1).
ограничивает трапецию с бесконечным
основание(рис. 1).

(Рис.1)
Если
несобственный интеграл
 сходится, то будем говорить, что
заштрихованная фигура имеет площадь,
равную этому интегралу. Если интеграл
расходится, то говорить о площади фигуры
нельзя.
сходится, то будем говорить, что
заштрихованная фигура имеет площадь,
равную этому интегралу. Если интеграл
расходится, то говорить о площади фигуры
нельзя.
Например,
бесконечной трапеции, ограниченной
положительной полуосью
 ,прямой
,прямой
 и линией
и линией
 ,можно приписать площадь, равную
,можно приписать площадь, равную
 ,ибо
,ибо

Бесконечной
трапеции, ограниченной гиперболой
 положительную полуосью
положительную полуосью
 и прямой
и прямой
 ,нельзя
приписать площадь, так как
,нельзя
приписать площадь, так как

Несобственные интегралы рассмотренного типа часто встречаются в задачах механики и электростатики в связи с определением потенциала.
Пусть
точка M
массы m,находящаяся
в начале координат, притягивает свободную
точку M1
массы 1,лежащую на расстоянии x
от M
на оси Величина P
силы
притяжения, как известно, определяется
по закону Ньютона
Величина P
силы
притяжения, как известно, определяется
по закону Ньютона

а
работа, произведенная при перемещении
M1
из точки
 в точку
в точку
 -по
формуле
-по
формуле

Знак минус перед интегралом взят потому, что направление силы противоположно направлению движения точки M (по той же причине работа оказалась отрицательной).
Если
удаляется в бесконечность ( ),то
),то

Если
точка M1
будет
перемещаться из бесконечности в точку
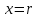 ,
то сила притяжения произведет уже
положительную работу:
,
то сила притяжения произведет уже
положительную работу:

Эта
работа называется потенциалом силы
притяжения материальной точки M
при
 (или в точке
(или в точке
 ).
).
Интегрирование несобственных интегралов по частям.
Пусть
на отрезке
 заданы
непрерывные функции
заданы
непрерывные функции и
и
 ,а
,а
 к
тому же имеет непрерывную производную.
Тогда, если обозначить через
к
тому же имеет непрерывную производную.
Тогда, если обозначить через
 какую-либо
первообразную от
какую-либо
первообразную от
 ,получим
,получим

Если существует несобственный интеграл
 ,
(2)
,
(2)
и существует предел

то существует несобственный интеграл

Отметим некоторые частные достаточные признаки существования интеграла (2) и предела (3), а следовательно интеграла (4).
1)Если функция

ограничена,
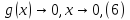
и
 ,
(7)
,
(7)
то интеграл (2) и предел (3) существуют. Действительно, тогда интеграл (2) сходится, причем абсолютно:


Таким
образом, в данном случае интеграл (4)
сходится и
 .
.
2) Признак Дирихле.
Пусть выполнены условия:
-
 и имеет на
и имеет на
 ограниченную первообразную, то есть
ограниченную первообразную, то есть
 ;
; -
Функция
 ,
,

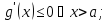
-

Пример
1. Интеграл
 имеет единственную особенность (в
«точке»
имеет единственную особенность (в
«точке»
 ).
Надо иметь в виду, что функция
).
Надо иметь в виду, что функция
 имеет устранимый разрыв в точке
имеет устранимый разрыв в точке
 .
Если ее положить равной 1 в этой точке,
то она станет непрерывной. Интеграл
.
Если ее положить равной 1 в этой точке,
то она станет непрерывной. Интеграл
 сходится потому, что интеграл
сходится потому, что интеграл
 сходится на основании признака Дирихле
(функция
сходится на основании признака Дирихле
(функция
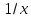 монотонно убывает, стремится при
монотонно убывает, стремится при к нулю и имеет непрерывную производную,
а функция
к нулю и имеет непрерывную производную,
а функция
 непрерывна
и имеет ограниченную первообразную
(
непрерывна
и имеет ограниченную первообразную
( )).
Однако интеграл
)).
Однако интеграл
 сходится не абсолютно:
сходится не абсолютно:

Вычисление интеграла

Вычислять данный интеграл будем по частям.


