Глава 2. Системы линейных уравнений.

§1. Основные понятия.

Определение 1. Системойmлинейных уравнений сnнеизвестными называется система вида:

, (I)

где и- числа.

Определение 2. Решением системы (I) называется такой набор неизвестных, при котором каждое уравнение этой системы обращается в тождество.

Определение 3. Система (I) называетсясовместной, если она имеет хотя бы одно решение инесовместной, если она не имеет решений. Совместная система называетсяопределенной, если она имеет единственное решение, инеопределеннойв противном случае.

Определение 4. Уравнение вида

называется нулевым, а уравнение вида

, где

называется несовместным. Очевидно, что система уравнений, содержащая несовместное уравнение, является несовместной.

Определение 5. Две системы линейных уравнений называютсяравносильными, если каждое решение одной системы служит решением другой и, наоборот, всякое решение второй системы является решением первой.

§2. Матричная запись системы линейных уравнений.

Рассмотрим систему (I) ( см.§1).

Обозначим:

- матрица коэффициентов при неизвестных

,

- матрица – столбец свободных членов

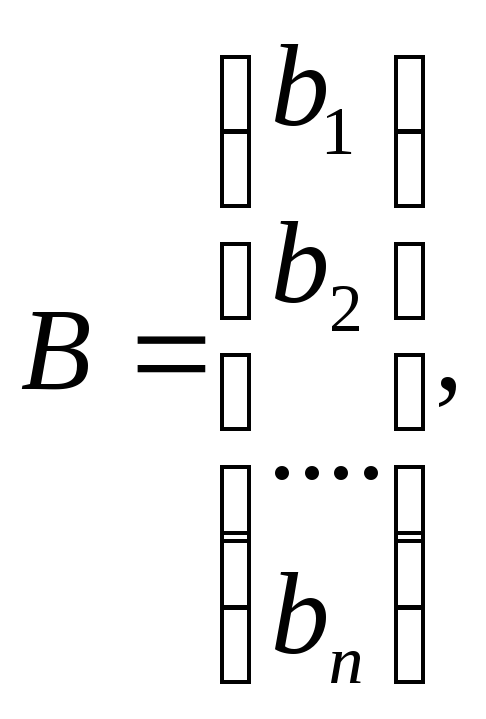
- матрица – столбец неизвестных

.

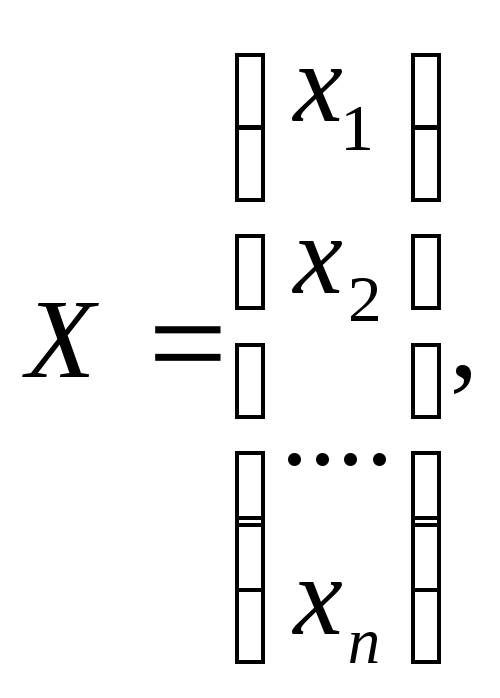
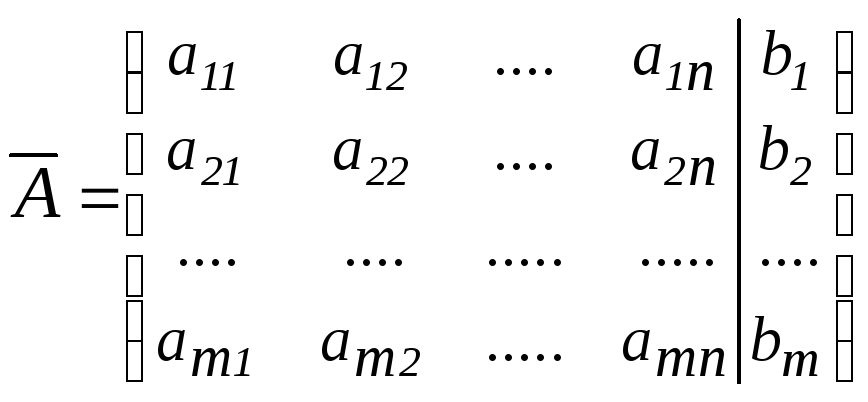Определение 1.Матрицаназываетсяосновной матрицей системы(I), а матрица- расширенной матрицей системы (I).

По определению равенства матриц системе (I) соответствует матричное равенство:

.

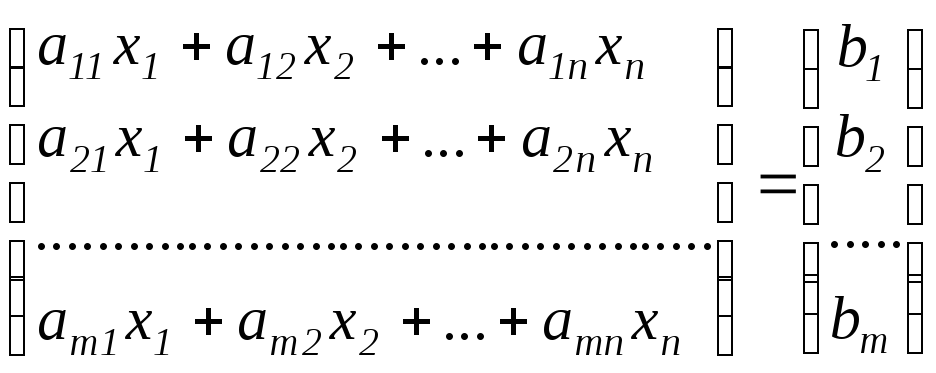Правую часть этого равенства по определению произведения матриц (см. определение 3 § 5 главы 1) можно разложить на множители:

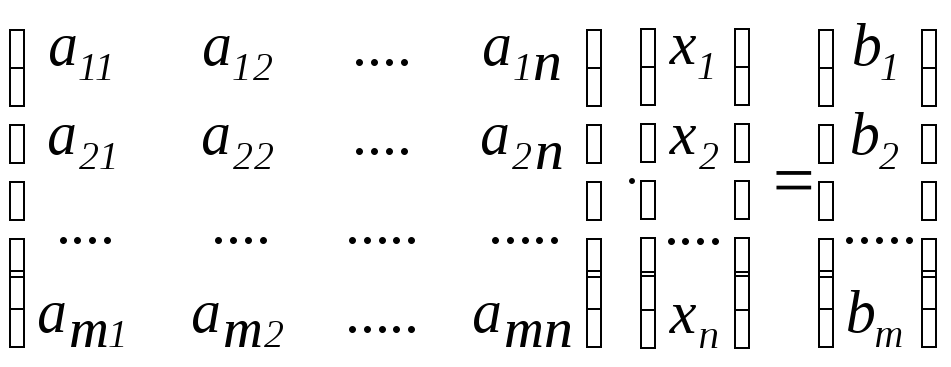, т.е.

.(2)

Равенство (2)называетсяматричной записью системы (I).

§ 3. Решение системы линейных уравнений методом Крамера.

Пусть в системе (I) ( см.§1) m=n, т.е. число уравнений равно числу неизвестных, и основная матрица системы невырожденная, т.е.. Тогда система (I) из §1 имеет единственное решение

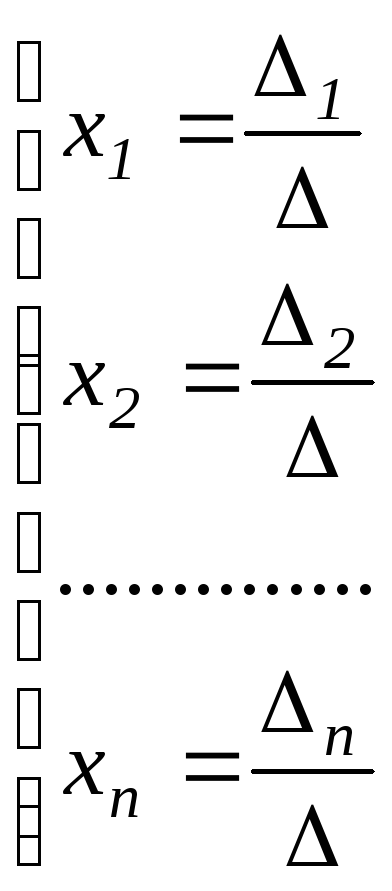,(3)

где Δ = det Aназывается главнымопределителем системы(I),Δ_iполучается из определителяΔ заменойi-го столбца на столбец из свободных членов системы (I).

Пример.

Решить систему методом Крамера :

.

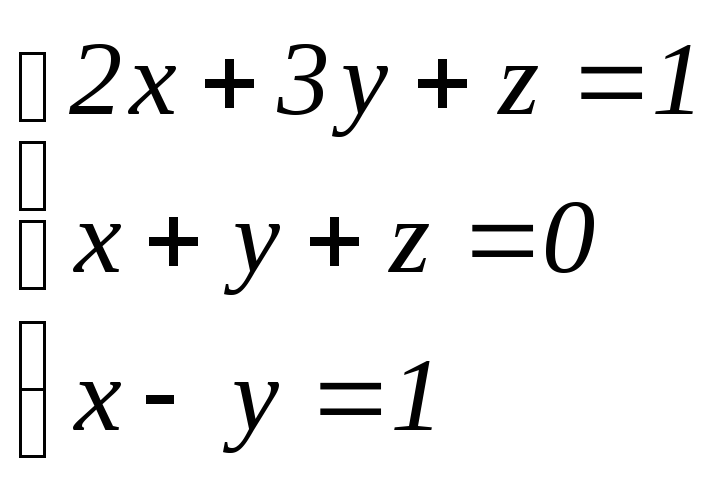По формулам (3) .

Вычисляем определители системы:

,

,

,

.

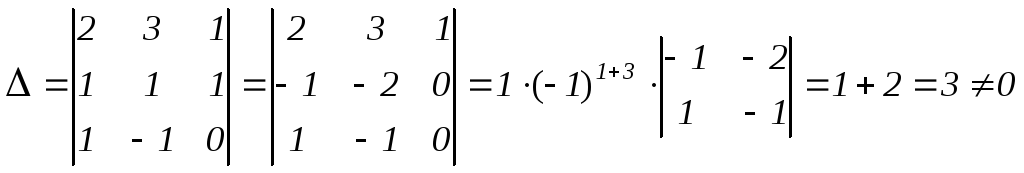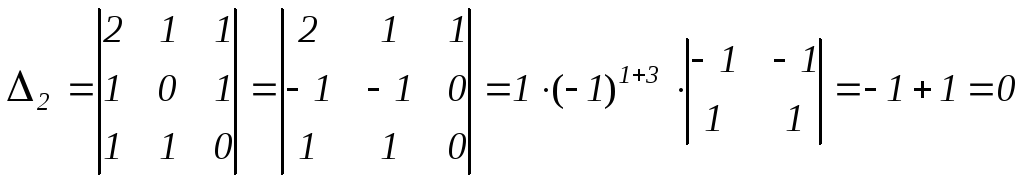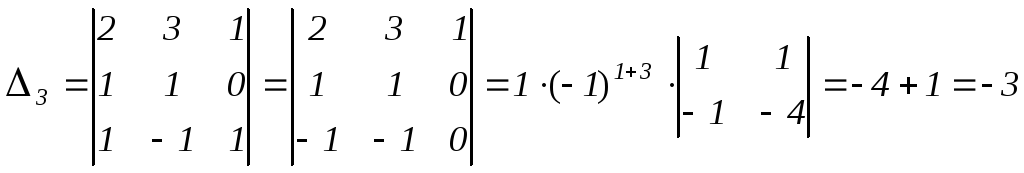Чтобы получить определитель , мы заменили в определителепервый столбец на столбец из свободных членов; заменяя в определителе2-ой столбец на столбец из свободных членов, получаем; аналогичным образом, заменяя в определителе3-ий столбец на столбец из свободных членов, получаем. Решение системы :

.

§ 4. Решение систем линейных уравнений с помощью обратной матрицы.

Пусть в системе (I) (см.§1)m=nи основная матрица системы невырожденная. Запишем систему (I) в матричном виде (см. §2):

,(2)

т.к. матрица Aневырожденная, то она имеет обратную матрицу(см. теорему 1 §6 главы 1). Умножим обе части равенства(2)на матрицу, тогда

.(3)

По определению обратной матрицы . Из равенства(3) имеем

,

отсюда

.(4)

Пример 1.

Решить систему с помощью обратной матрицы

.

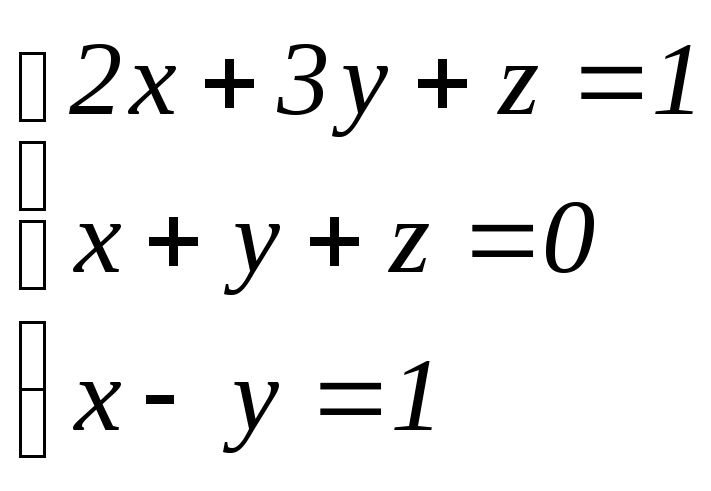Обозначим

;;.

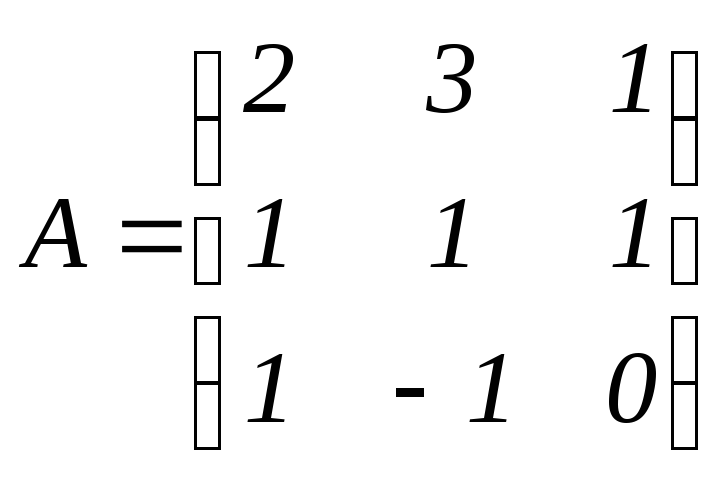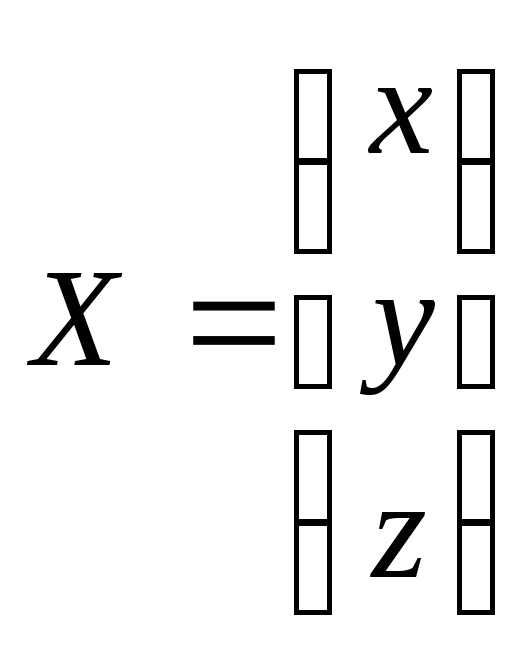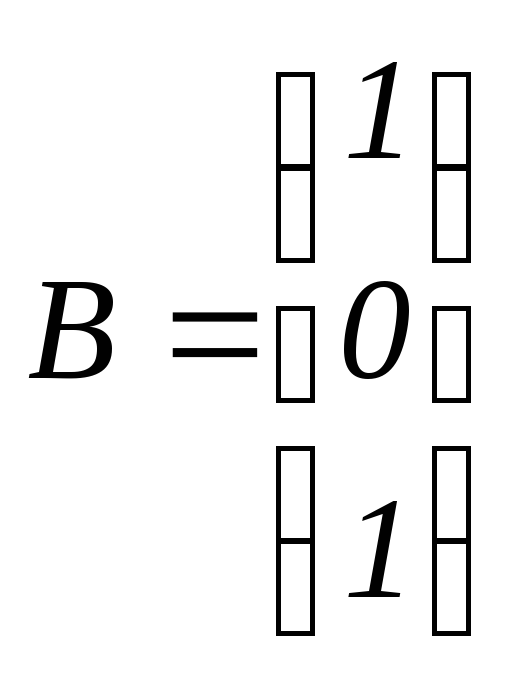В примере (§ 3) мы вычислили определитель, следовательно, матрицаAимеет обратную матрицу. Тогда в силу(4)

, т.е.

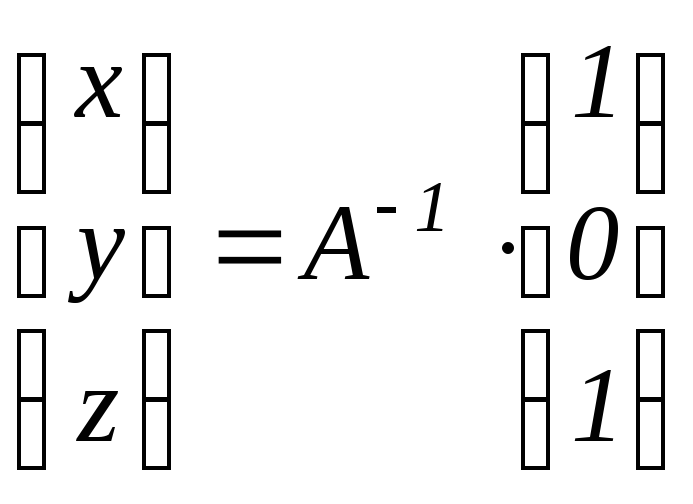.(5)

Найдем матрицу (см.§6 главы 1)

,,,

,,,

,,,

,

.

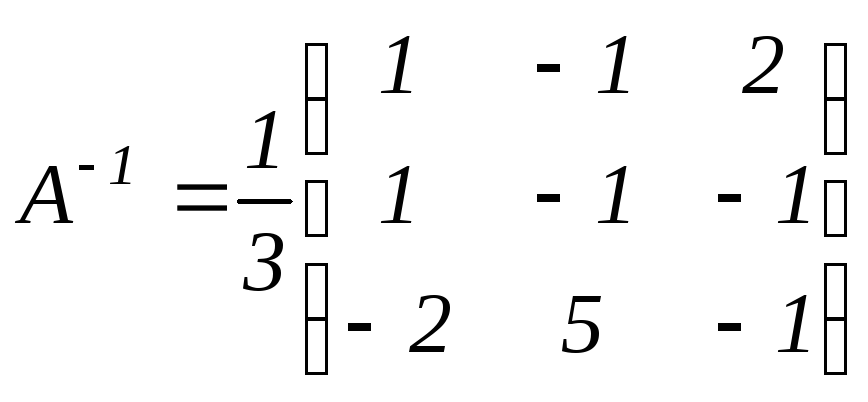Ответ: