- •МинИстерство сельского хозяйства рф
- •Содержание
- •Введение
- •Тема 1. «однофакторные корреляционно - регрессионные модели и возможности их применение при анализе социально-экономических систем ».
- •1.1. Методические указания
- •1.2. Типовой пример выполнения индивидуальной работы по теме 1
- •1.3. Варианты заданий индивидуальной работы по теме 1
- •Тема 2. Анализ и прогнозирование временных рядов
- •Методические указания
- •2.2. Технология решения задач корреляционно-регрессионного анализа временных моделей
- •2.3. Типовой пример выполнения индивидуальной работы по теме 2.
- •Варианты заданий индивидуальной работы по теме 2
- •Список рекомендуемой литературы:
2.2. Технология решения задач корреляционно-регрессионного анализа временных моделей
Формирование исходной базы данных
Построение модели начинают с решения вопроса о спецификации модели. Во множественной регрессии спецификация модели включает в себя решение двух вопросов:
отбор факторов
выбор вида уравнения.
Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя с другими жизненными явлениями.
Факторы, включенные в модель должны отвечать следующим требованиям:
должны быть количественно измеримы; если необходимо включать качественный фактор, то ему необходимо придать количественное определение.
не должны быть интеркоррелированны (т.е. факторные признаки не должны находится в тесной зависимости между собой) и находится в точной функциональной связи. При включении в модель факторов с высокой интеркорреляцией может привести к нежелательным последствиям, т.е. система норм уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
Отбор факторов производится на основе качественного теоретико-экономического анализа и проходит в 2 стадии:
подбираются факторы, исходя из сущности проблемы,
на основе матрицы показателей корреляции определяют t–статистики для параметров регрессии.
Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, то коллинеарность факторов нарушает это условие. Коллинеарность может возникать в силу различных причин. Например, несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания.
Коэффициенты
интеркорреляции (т.е. корреляции между
факторными признаками) позволяют
исключить из модели факторы, дублирующие
друг друга. Считается, что 2 переменные
являются коллинеарными,
т.е. находятся между собой в линейной
зависимости, если коэффициент
![]()
Если факторы явно коллинеарны, то они дублируют друг друга и один из них необходимо исключить из модели.
Правило: предпочтение отдается не фактору, который более тесно связан с результатом, а тому фактору, который при достаточной связи с результатом имеет минимальную тесноту связи с другими факторами.
С целью выявления факта коллинеарности факторов составляется матрица парных коэффициентов корреляции, измеряющих тесноту связи каждого из факторов-признаков с результатом и между собой.
Таблица 2.1. – Матрица парных коэффициентов корреляции
|
Признак |
У |
Х1 |
… |
Хm |
|
У |
1 |
rYX1 |
… |
RYXm |
|
Х1 |
rYX1 |
1 |
… |
rX1Xm |
|
… |
… |
… |
… |
… |
|
Хm |
rYXm |
RX1Xm |
… |
1 |
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем 2 фактора связаны между собой линейной зависимостью, т.е. наблюдается совокупность воздействия факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценивать влияние каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка параметров с помощью МНК.
Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов «в чистом» виде, т.к. факторы интерколлинеарны. Параметры линейной регрессии теряют жизненный смысл.
оценки параметров ненадежны, обнаруживаются большие стандартные ошибки и меняют с изменением объема наблюдений не только по величине, но и по знаку, что делает модель непригодной для анализа и прогноза.
Выбор вида модели и оценка ее параметров
Как и в парной зависимости возможны различные виды множественной регрессии: линейные и нелинейные. В виду четкой интерпретации параметров наиболее широко используются линейная и степенные функции.
В уравнении множественной регрессии:
![]() (41)
(41)
Коэффициенты при переменных х называются коэффициентами «чистой» регрессии. Они показывают среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
Параметр а не подлежит экономической интерпретации.
Анализ уравнения регрессии и методика определения его параметров становятся более наглядными, а расчеты существенно упрощаются, если воспользоваться матричной формой записи этого уравнения. Так, уравнения вида
![]() (42)
(42)
можно записать следующим образом:
![]() ,
,
где Y – вектор зависимой переменной размерности (n х 1), представляющий собой n наблюдений значений yt.
X – матрица независимых переменных, элементы которой суть n x m наблюдения значений независимых переменных X1, X2, …, Xm размерность данной матрицы равна (n x m);
α – подлежащий оцениванию вектор неизвестных параметров размерности (m х 1);
ε – вектор случайных отклонений (возмущений) размерности (n х 1).
Таким образом,
|
|
Х = |
1 1 x21 .... x2m .... .... .... .... 1 xn1 .... xnm |
|
Уравнение (42) содержит значения неизвестных параметров α0, α1, α2, … , αm . эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров представлены их оценки (а именно такие регрессии и применяются на практике), имеют вид:
![]() (43)
(43)
где α – вектор оценок параметров;
ε – вектор «оцененных» отклонений регрессии, ε = Y – Xα – остатки регрессии;
![]() –оценка
значений Y,
равная Xα.
–оценка
значений Y,
равная Xα.
Для оценивания неизвестного вектора параметров α воспользуемся методом наименьших квадратов (МНК). Формула для вычисления параметров регрессионного уравнения имеет вид:
α = (ХТХ)-1ХТУ (44)
Можно воспользоваться и другим способом оценки неизвестных параметров регрессионного уравнения.
Для линейных моделей и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которых позволяет получить оценки параметров регрессии:
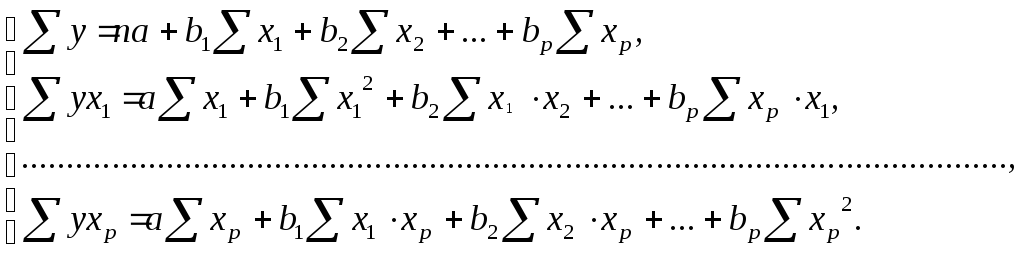
![]() (45)
(45)
для ее решения может быть применен метод определителей:
![]() (46)
(46)
где
![]()
 - определитель системы.
- определитель системы.
![]() -
частные определители; которые получаются
путем замены соответствующего столбца
матрицы определителя системы данными
левой части системы.
-
частные определители; которые получаются
путем замены соответствующего столбца
матрицы определителя системы данными
левой части системы.
Для оценки параметров нелинейных уравнений используют 2 подхода:
основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменный исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.
обычно применяют в случае, когда подобрать соответствующее линеаризационное преобразование невозможно. В этом случае применяют методы нелинейной оптимизации на основе исходных переменных.
Коэффициенты условно чистой регрессии, т.е. bj являются именованными числами, выраженными в различных единицах измерения, в тех же единицах, что и соответствующие им факторы. Поэтому они не сравнимы друг с другом, т.е. по их величине нельзя сделать вывод, какой из факторов в наибольшей степени влияет на результат. Для приведения их в сравнимый вид применяется то же преобразование, что и для получения парных коэффициентов. Полученную величину называют стандартизированным коэффициентом регрессии.
Стандартизированный коэффициент регрессии рассчитывается по формуле
![]() (47)
(47)
βj – коэффициент при факторе хj. определяет силу влияние вариации хj на вариацию результативного признака у при отвлечении от сопутствующего влияния вариаций других факторов, входящих в уравнение регрессии.
Т.к. βj сравнимы между собой, то по величине данных коэффициентов можно ранжировать факторы по силе их воздействия на результат.
Смысл стандартизированных коэффициентов βj позволяет использовать их при отсеве факторов, т.е. из модели исключаются факторы с наименьшим значением βj.
Коэффициенты условно чистой регрессии можно выразить в виде относительно сравнимых показателей связи – средних коэффициентов эластичности.
![]() (48)
(48)
Средний коэффициент эластичности показывает, что при изменении фактора хj на 1% результативный признак изменяется на Эj % его средней величины при неизмененном влиянии всех остальных факторов.
Проверка качества модели
Качество модели оценивается по адекватности и точности на основе анализа остатков регрессии . Анализ остатков позволяет получить представление о том, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны «вести себя» как независимые (в действительности почти независимые), одинаково распределенные случайные величины. В классических методах регрессионного анализа предполагается нормальный закон распределения.
Исследование остатков полезно начинать с их графика. Нередко встречаются ситуации, когда остатки содержат тенденцию или подвержены циклическим колебаниям. В этом случае говорят о наличии автокорреляции остатков. Иногда автокорреляция связана с исходными данными и вызвана наличием ошибок измерения результативного признака. В других случаях автокорреляция указывает на наличие какой-то достаточно сильной зависимости, неучтенной в модели. Например, при подборе простой линейной зависимости график остатков может показать необходимость перехода к нелинейной модели или включения в модель периодических компонент.
Существуют два наиболее распространенных метода определения автокорреляции остатков:
построения графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции;
использование критерия Дарбина–Уотсона (приложение 3) и расчет величины
 (49)
(49)
Таким образом, d это отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Коэффициент автокорреляции остатков определяется по
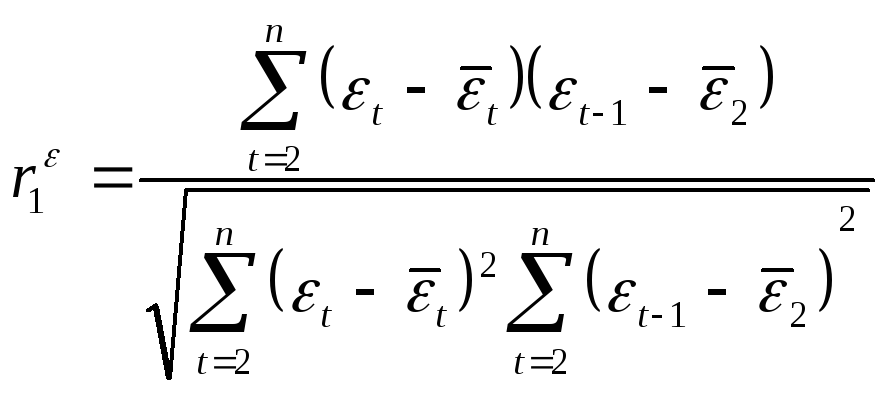 (50)
(50)
|
|
|
Если в остатках существует полная положительная автокорреляция и r1 ε = 1, то d = 0. если в остатках полная отрицательная автокорреляция и r1 ε = -1, то d = 4.
Таким образом, величина d изменяется в переделах:
0 d 4.
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина–Уотсона следующий: выдвигается гипотеза Но об отсутствии автокорреляции остатков; альтернативные гипотезы Н1 и Н1 состоят соответственно в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (приложение 3) определяются Критические значения критерия Дарбина-Уотсона dL и du для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости . По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Вопрос о принятии или отклонении каждой из гипотез с вероятностью (1-) рассматривается в соответствии с рис. 2.1.
|
Е Но отклоняется. С вероятностью Р=(1-) принимается Н1 |
Зона неопре деленнос ти |
Нет оснований отклонять Но (автокорреляция остатков отсутствует) |
Зона неопре деленнос ти |
Есть отрицательная автокорреляция остатков. Но отклоняется. С вероятностью Р=(1-) принимается Н1 |
0 dL du 2 4- du 4- dL 4
Рис. 2.1. Механизм проверки гипотезы о наличии автокорреляции остатков
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то нельзя сделать окончательный вывод по этому критерию.
Выбросы. График остатков хорошо показывает и резко отклоняющиеся от модели наблюдения– выбросы. Подобным аномальным наблюдениям надо уделять особо пристальное внимание, так как их присутствие может грубо искажать значение оценок. Устранение эффектов выбросов может проводится либо с помощью удаления этих точек из анализируемых данных (эта процедура называется цензурированием), либо с помощью применения методов оценивания параметров, устойчивым к подобным грубым отклонениям.
Кроме рассмотренных выше характеристик, целесообразно использовать коэффициент множественной корреляции и детерминации.
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
![]()
![]() (51)
(51)
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:
![]()
![]()
![]()
![]() (52)
(52)
Существует 2 способа вычисления R2:
через корреляционное отношение
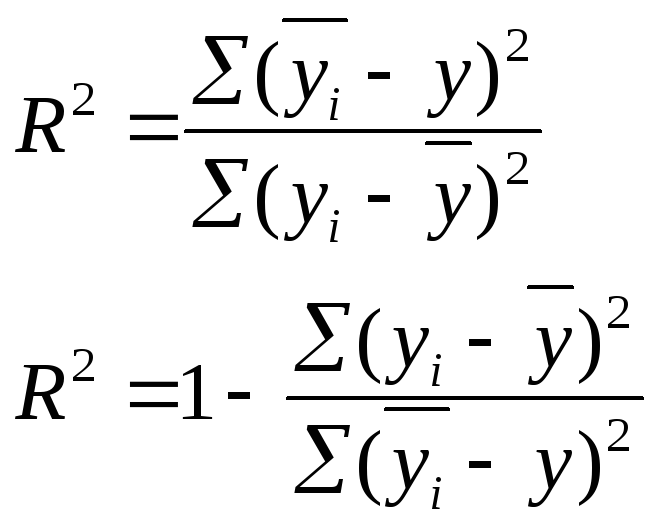 (53)
(53)
Данный способ рационален в то случае, если n мало.
через определители матрицы.
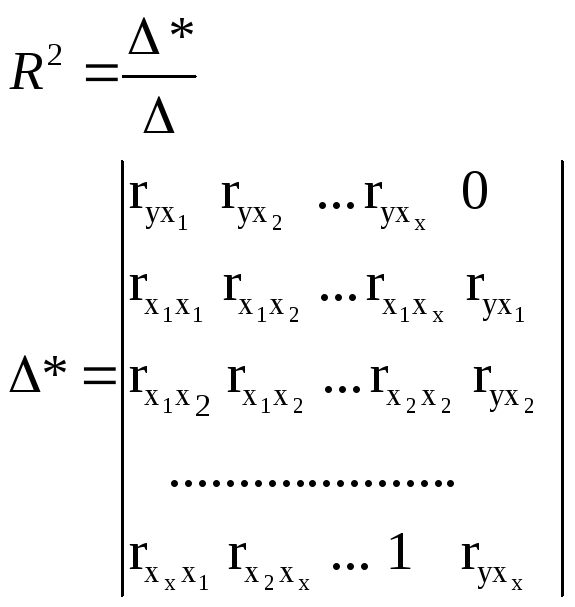 (54)
(54)
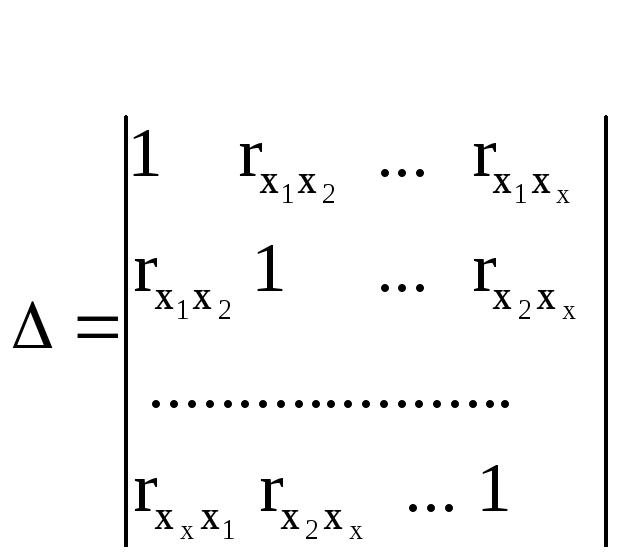 (55)
(55)
в многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, этот коэффициент должен быть скорректирован с учетом числа независимых переменных.
В связи с этим необходимо корректировать коэффициент множественной детерминации на потерю степеней свободы вариации.
![]() (56)
(56)
Скорректированный
коэффициент
![]() всегда ниже, чем нескорректированный.
Исключение слабого фактора всегда
снижает некорректируемый коэффициент
детерминации, поэтому мы не можем сделать
точный вывод о целесообразности
исключения данного фактора из модели
поR2.
всегда ниже, чем нескорректированный.
Исключение слабого фактора всегда
снижает некорректируемый коэффициент
детерминации, поэтому мы не можем сделать
точный вывод о целесообразности
исключения данного фактора из модели
поR2.
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
![]() (57)
(57)
Частный F-критерий оценивает статистическую значимость присутствия каждого их факторов в уравнении. В общем виде для фактора xi частный F-критерий определиться как
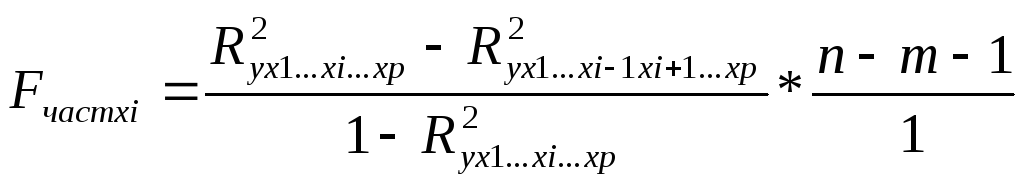 (58)
(58)
Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводиться к вычислению значения
![]() (59)
(59)
где mbi – средняя квадратическая ошибка коэффициента регрессии bi, она может быть определена как
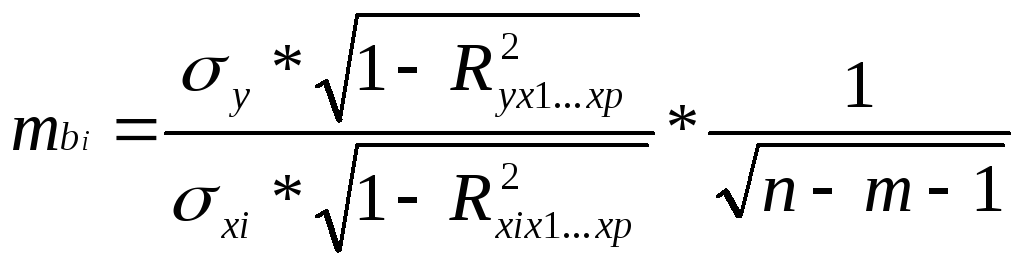 (60)
(60)
Методика проверки значимости уравнения регрессии в целом и отдельных его параметров такая же, как и в парной регрессии.
Использование многофакторных моделей для анализа и прогнозирования развития экономических систем
Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Обычно термин «прогнозирование» используется в тех ситуациях, когда требуется предсказать состояние системы в будущем. Для регрессионных моделей он имеет более широкое значение. Как уже отмечалось, данные могут не иметь временной структуры, но и в этих случаях вполне может возникнуть задача оценки значения зависимой переменной для некоторого набора независимых, объясняющих переменных, которых нет в исходных наблюдениях. Именно в этом смысле – как построение оценки зависимой переменной – и следует понимать прогнозирование в эконометрике.
Проблема прогнозирования имеет много различных аспектов. Различают точечное и интервальное прогнозирование. В первом случае оценка – это конкретное число, во втором – интервал, в котором истинное значение переменной находится с заданным уровнем доверия. Кроме того, для временных рядов при нахождении прогноза существенно наличие или отсутствие корреляции по времени между ошибками.
При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.
Для прогнозирования зависимой переменной на l шагов вперед необходимо знать прогнозные значения всех входящих в нее факторов. Их оценки могут быть получены МНК или на основе временных экстраполяционных моделей или заданы пользователем. Эти оценки подставляются в модель, и получаются прогнозные оценки.
Для
того, чтобы определить область возможных
значений результативного показателя
при рассчитанных значениях факторов,
следует учитывать два возможных
источников ошибок: ошибки, обусловленные
рассеиванием наблюдений относительно
линии регрессии и ошибки, обусловленные
математическим аппаратом построения
самой линии регрессии. Ошибки первого
рода измеряются с помощью характеристик
точности, в частности, величиной
![]() .
.
Ошибки второго рода обусловлены фиксацией численного значения коэффициентов регрессии, в то время как они в действительности являются случайными, нормально распределенными.
Для линейной модели доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения U от линии регрессии:
U(l)=![]() , (61)
, (61)
![]() (62)
(62)
Доверительный интервал прогноза имеет границы:
верхняя
граница прогноза:
![]() ,
,
нижняя
граница прогноза:
![]() ,
,
Если построенная регрессионная модель адекватна и прогнозные оценки факторов достаточно надежны, то с заданным уровнем значимости можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадает в интервал, образованный нижней и верхней границами.

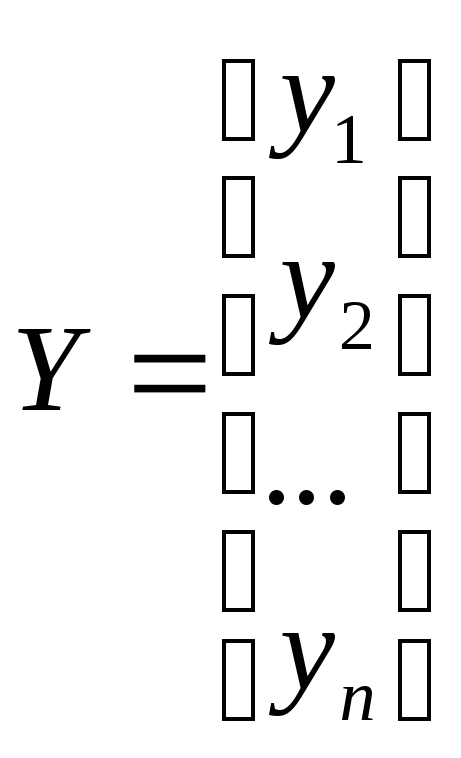

 x11
.... x1m
x11
.... x1m