
- •Глава II. Векторная алгебра
- •§ 1. Векторы и основные линейные операции над ними
- •1. Векторные величины
- •2. Умножение вектора на скаляр
- •3. Единичный вектор
- •4. Сложение векторов
- •5. Вычитание векторов
- •§2. Линейная зависимость и независимость векторов. Базисы на плоскости и в пространстве. Прямоугольная декартова система координат
- •1. Линейная зависимость и независимость векторов
- •2. Базисы на плоскости и в пространстве
- •3. Прямоугольная декартова система координат
- •§3. Проекция вектора на ось. Координаты вектора. Компоненты вектора.
- •1. Проекция вектора на ось.
- •2. Компоненты вектора по координатным осям и координаты точки.
- •§ 4 Теоремы о проекциях вектора.
- •§ 5. Скалярное произведение и его свойства
- •1. Определение скалярного произведения
- •2. Необходимое и достаточное условие ортогональности двух векторов
- •3. Скалярное произведение векторов, заданных своими координатами
- •В силу свойства 4 получим
- •4. Угол между двумя векторами
- •§ 6. Векторное произведение и его свойства
- •1. Определение векторного произведения
- •2. Необходимое и достаточное условие коллинеарности двух ненулевых векторов
- •3. Векторное произведение векторов, заданных своими координатами
- •4. Механический смысл векторного произведения
- •§ 7. Смешанное произведение трёх векторов
- •2. Свойства смешанного произведения
- •§ 8. Двойное векторное произведение
5. Вычитание векторов
Рис. 3






 Определение
5. Вектор
Определение
5. Вектор
![]() называется
разностью векторов
называется
разностью векторов![]() и
и![]() ,
т.е.
,
т.е.![]() ,
если
,
если![]() .
Отсюда следует, что
.
Отсюда следует, что![]() т.е. вычитание векторов сведено к сложению
(рис.2.1.4). Нетрудно заметить,
что разность век-
т.е. вычитание векторов сведено к сложению
(рис.2.1.4). Нетрудно заметить,
что разность век-
торов лежит
на второй диагонали параллелограмма,
построенного на векторах
![]() и
и![]() ,
проведённой из конца вектора -
,
проведённой из конца вектора -![]() в конец вектора
в конец вектора![]() .
.
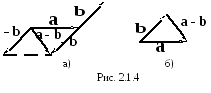
§2. Линейная зависимость и независимость векторов. Базисы на плоскости и в пространстве. Прямоугольная декартова система координат
1. Линейная зависимость и независимость векторов
Пусть
имеется nвекторов![]() ,
,![]() ,
…,
,
…,![]() и
и![]() постоянных коэффициентов
постоянных коэффициентов![]() ,
,
![]() ,…,
,…,![]() .Выражение
.Выражение
![]() называется
линейной комбинацией векторов
называется
линейной комбинацией векторов![]() ,
,![]() ,
…,
,
…,![]() .
.
Определение
1.Векторы![]() ,
,![]() ,
…,
,
…,![]() называютсялинейно зависимыми,
если существуют числа
называютсялинейно зависимыми,
если существуют числа![]() ,
,
![]() ,…,
,…,![]() ,
из которых хотя бы одно отлично от
нуля, такие, что линейная комбинация
равна нулю:
,
из которых хотя бы одно отлично от
нуля, такие, что линейная комбинация
равна нулю:
![]()
Определение
1*. Векторы
![]() ,
,![]() ,
…,
,
…,![]() называются линейно
зависимыми, если
хотя бы один вектор из этой системы
можно выразить в виде линейной комбинации
остальных.
называются линейно
зависимыми, если
хотя бы один вектор из этой системы
можно выразить в виде линейной комбинации
остальных.
Можно доказать, что определения 1 и 1*эквивалентны, т.е. из 1 следует 1*и наоборот.
Определение
2. Векторы
![]() ,
,![]() ,
…,
,
…,![]() называются линейно
независимыми, если
линейная комбинация
называются линейно
независимыми, если
линейная комбинация
![]() лишь при условии
лишь при условии![]() .
.
Определение
2*.Векторы![]() ,
,![]() ,
…,
,
…,![]() называютсялинейно независимыми,
если ни один из этих векторов нельзя
представить в виде линейной комбинации
остальных.
называютсялинейно независимыми,
если ни один из этих векторов нельзя
представить в виде линейной комбинации
остальных.
Можно доказать, что определения 2 и 2* эквивалентны.
Пример
1.
Доказать, что
коллинеарные векторы линейно зависимы.
Действительно, поместим векторы
![]() и
и![]() на одной прямой (рис. 2.2.1), тогда можно
найти такое
на одной прямой (рис. 2.2.1), тогда можно
найти такое![]() ,
при котором
,
при котором![]() =>
=>![]() ,
а это и означает, что
,
а это и означает, что![]() иbлинейно зависимы.
иbлинейно зависимы.
Пример 2. Доказать, что любые три вектораa,b иc, лежащие в плоскости, линейно зависимы.
Действительно, поместим начало всех
трёх векторов в общую точку (рис.2.2.2).
Очевидно, тогда можно подобрать
единственную пару чисел
![]()
![]() и
и![]() ,
так что будет
,
так что будет![]() ,
а что и означает, что векторы
,
а что и означает, что векторы![]() ,
,![]() и
и![]() линейно
зависимы.
линейно
зависимы.

Определение 3. Три ненулевых вектора называютсякомпланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Итак, мы показали, что компланарные векторы линейно зависимы.
Пример 3. Любые четыре вектора в пространстве линейно зависимы.
Действительно,
можно подобрать, причём единственным
образом, такие числа
![]() ,
,![]() ,
,![]() ,
что будет
,
что будет![]() (рис. 2.2.3).
(рис. 2.2.3).

2. Базисы на плоскости и в пространстве
Определение
1.Совокупность любых
двух линейно независимых векторов,
принадлежащих данной плоскости,
называетсябазисом на этой плоскости.
Если![]() ,
,![]() - базис на плоскости, то для любого
вектора
- базис на плоскости, то для любого
вектора![]() ,
лежащего в этой плоскости, можно найти
единственным образом такие числа
,
лежащего в этой плоскости, можно найти
единственным образом такие числа![]() и
и![]() ,
что будет
,
что будет![]() .
Числа
.
Числа![]() и
и![]() называются координатами вектора
называются координатами вектора![]() в данном базисе.
в данном базисе.
Определение
2. Совокупность любых трёх
линейно независимых векторов![]() ,
,![]() ,
,![]() в пространстве называетсябазисом
в пространстве. Если
в пространстве называетсябазисом
в пространстве. Если![]() - произвольный вектор, то всегда можно
найти единственным образом числа
- произвольный вектор, то всегда можно
найти единственным образом числа![]() ,
,![]() ,
,![]() такие, что будет иметь место представление:
такие, что будет иметь место представление:![]() .
Коэффициенты
.
Коэффициенты![]() ,
,![]() ,
,![]() в разложении данного вектора по базису
называются координатами вектора
в разложении данного вектора по базису
называются координатами вектора![]() в базисе
в базисе![]() ,
,![]() ,
,![]() .
.
3. Прямоугольная декартова система координат
Из всех возможных базисов
(![]() ,
,![]() ,
,![]() )в пространстве выберем
такой, чтобы все векторы, входящие в
этот базис, были попарно ортогональны
(т.е.
)в пространстве выберем
такой, чтобы все векторы, входящие в
этот базис, были попарно ортогональны
(т.е.
![]() ,
(
,
(![]() ,
далее разделим каждый вектор базиса на
его длину. Получим базис
,
далее разделим каждый вектор базиса на
его длину. Получим базис ![]() ,
,![]() ,
,![]() Такой базис называется
ортонормированным.
Такой базис называется
ортонормированным.
Определение.
Тройка векторов![]() ,
,
![]() ,
,![]() называетсяправой, если при
наблюдении с конца вектора
называетсяправой, если при
наблюдении с конца вектора![]() кротчайший поворот от вектора
кротчайший поворот от вектора![]() к вектору
к вектору![]() происходит против движения часовой
стрелки.
происходит против движения часовой
стрелки.
Ограничимся выбором правой тройки
базисных векторов
![]() ,
,![]() ,
,![]() .Поместим далее начало
векторов, входящих в выбранной базис,
в общую точку 0 и из этой точки проведём
оси Ox,
Oy,
Oz,
направления которых
совпадают с направлениями векторов
.Поместим далее начало
векторов, входящих в выбранной базис,
в общую точку 0 и из этой точки проведём
оси Ox,
Oy,
Oz,
направления которых
совпадают с направлениями векторов ![]() ,
,![]() ,
,![]() .
.
Получим так называемую
пространственную прямоугольную
правую декартову систему координат
Oxyz.
Причём принято орты обозначать так:
![]() ,
,![]() ,
,![]() (рис. 2.2.4). ОсьOx
называется осью
абсцисс, ось Oy
– осью ординат,
ось Oz
– осью аппликат.
(рис. 2.2.4). ОсьOx
называется осью
абсцисс, ось Oy
– осью ординат,
ось Oz
– осью аппликат.
Если
![]() ,
получим прямоугольную правую систему
декартовых координат на плоскости –
системуOxy.
,
получим прямоугольную правую систему
декартовых координат на плоскости –
системуOxy.
![]()


![]()
![]()
![]()



![]()
![]()

Рис. 2.2.4
