
dm_tema_1
.pdf
1. Теория множеств |
1.4 Отношения |
Пример
На множестве чисел A = f1; 2; 3; 4; 5; 6g зададим бинарное отношение
R = f(x; y)j x делитель yg:
Отношение содержит элементы
R = f(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6);
(2; 2); (2; 4); (2; 6); (3; 3); (3; 6); (4; 4); (5; 5); (6; 6)g:
Матрица отношения равна
23
1 |
1 |
1 |
1 |
1 |
1 |
60 |
1 |
0 |
1 |
0 |
17 |
67
|
0 |
0 |
1 |
0 |
0 |
1 |
|
MR = |
60 0 |
0 1 |
0 |
07 |
: |
||
|
60 |
0 |
0 |
0 |
1 |
07 |
|
|
6 |
|
|
|
|
7 |
|
|
60 |
0 |
0 |
0 |
0 |
17 |
|
|
4 |
|
|
|
|
5 |
|
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
31 / 65 |
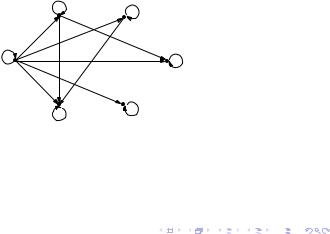
1. Теория множеств |
1.4 Отношения |
Граф отношения
|
2 |
3 |
|
|
|
1 |
|
4 |
|
6 |
5 |
|
|
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
32 / 65 |

1. Теория множеств |
1.4 Отношения |
Определение
Тождественным отношением, заданным на множестве A, называется
отношение
E = f(x; x)j x 2 Ag :
Матрица тождественного отношения, заданного на конечном множестве, есть единичная матрица.
Определение
Множество
DR = fxj xRyg A
называется областью определения отношения R A B.
Определение
Множество
IR = fyj xRyg B
называется областью значений отношения R A B.
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
33 / 65 |

1. Теория множеств |
1.4 Отношения |
Определение
Обратным отношением для отношения R A B называется
отношение
R 1 = f(y; x)j xRyg B A:
Определение Композицией бинарных отношений
R1 A B; R2 B C
называется отношение
R1 R2 = f(x; y)j x 2 A; y 2 C; 9z 2 B : xR1z; zR2yg A C :
Определение
Ядром отношения R A B называется отношение
KR = R R 1:
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
34 / 65 |

1. Теория множеств |
1.4 Отношения |
Свойства операций над бинарными отношениями:
1)R 1 1 = R
2)(R1 [ R2) 1 = R1 1 [ R2 1
3)(R1 \ R2) 1 = R1 1 \ R2 1
4)R1 (R2 R3) = (R1 R2) R3
5)R1 (R2 [ R3) = (R1 R2) [ (R1 R3)
6)(R1 [ R2) R3 = (R1 R3) [ (R2 R3)
7)(R1 R2) 1 = R2 1 R1 1
Докажем свойство 7
x(R1 R2) 1y , y(R1 R2)x , 9z : yR1z; zR2x , zR1 1y; xR2 1z , x(R2 1 R1 1)y:
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
35 / 65 |

1. Теория множеств 1.4 Отношения
Пусть R бинарное отношение на множестве A. Обозначим
Rn = R R R :
R |
|
= E . Тогда |
| |
|
{z |
|
} |
|
|
|
|
|
n |
|
|
Определим |
0 |
|
справедливы следующие соотношения |
||||
Rn Rm = Rn+m; |
(Rn) 1 = R 1 n = R n: |
||||||
Определение
Отношение R A2 называется рефлексивным, если
8x 2 A : xRx:
Определение
Отношение R называется антирефлексивным, если не существует x 2 A такого, что xRx.
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
36 / 65 |

1. Теория множеств |
1.4 Отношения |
Определение
Отношение R A2 называется симметричным, если
8x; y 2 A : xRy ) yRx:
Определение
Отношение R называется антисимметричным, если не существует x; y 2 A таких, что одновременно xRy è yRx.
Определение
Отношение R A2 называется транзитивным, если для
8x; y; z 2 A : xRy; yRz ) xRz:
Определение
Отношение R A2 называется плотным, если
8x; y 2 A : x 6= y; xRy ) 9z 6= x; y : xRz; zRy:
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
37 / 65 |

1. Теория множеств |
1.4 Отношения |
Теорема
Отношение R симметрично , R = R 1
Доказательство.
Необходимость. Пусть R симметрично. Тогда
xRy ) yRx ) xR 1y ) R R 1;
xR 1y ) yRx ) xRy ) R 1 R:
Следовательно, R = R 1. Достаточность. Пусть R = R 1. Тогда
xRy ) xR 1y ) yRx:
Следовательно, R симметрично.
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
38 / 65 |

1. Теория множеств |
1.4 Отношения |
Теорема
Отношение R транзитивно , R2 R.
Доказательство.
Необходимость. Пусть R транзитивно. Тогда
8x; y : xR2y ) 9z : xRz; zRy ) xRy ) R2 R:
Достаточность. Пусть R2 R. Тогда
8x; y; z : xRz; zRy ) xR2y ) xRy:
Следовательно, отношение транзитивно.
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
39 / 65 |

1. Теория множеств |
1.4 Отношения |
Теорема
Транзитивное отношение R плотно , R2 = R.
Доказательство.
Необходимость. Пусть R плотно. Тогда
8x; y : xRy ) 9z : xRz; zRy ) xR2y ) R R2:
В силу транзитвности R2 R. Следовательно, R2 = R. Достаточность. Пусть R2 = R. Тогда
8x; y : xRy ) xR2y ) 9z : xRz; zRy:
Следовательно, R плотно.
Е.А.Перепелкин (АлтГТУ) |
Дискретная математика. Тема 1 |
2012 |
40 / 65 |
