
учебник(математика)
.pdf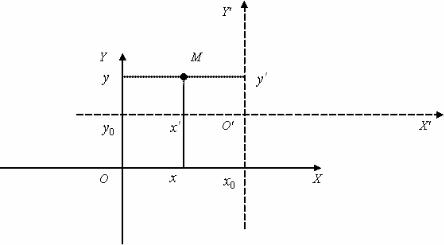
5. Приведение кривых второго порядка к каноническому виду
5.1. Преобразование систем координат
Сдвиг системы координат
Сдвигом системы координат называется преобразование, при котором ее начало переносится в другую точку с сохранением направления осей исход- ной системы координат.
Рис. 5.1.
На рис. 5.1. показана исходная система координат K = OXY и система |
|||
координат K′ = O′X′Y′ , полученная из системы K путем переноса ее начала |
|||
координат O в точку O′ с координатами (x0 , y0 ). Точка M в системе K |
|||
имеет координаты (x, y), а в системе K′ |
— (x′, y′). На рис. 5.1. непосредст- |
||
венно видно, что эти координаты связаны соотношениями |
|||
x′ = x − x0 |
, |
x = x′ + x0 |
. |
а) |
б) |
||
y′ = y − y0 |
|
y = y′ + y0 |
|
Эти взаимно обратные соотношения и описывают преобразование сдвига системы координат: формулы (а) выражают координаты точки M в систе- ме K′ , сдвинутой относительно системы K в точку (x0 , y0 ), тогда как фор- мулы (б) — координаты точки M в системе K , сдвинутой относительно сис- темы K′ в точку (− x0 , − y0 ).
Поворот системы координат
Поворотом системы координат называется преобразование K → K′ , при котором оси исходной системы K поворачиваются вокруг начала координат на некоторый угол ϕ . Угол поворота отсчитывается от оси OX в направле- нии против часовой стрелки.
51

Рис. 5.2.
На рис. 5.2. видно, что координата x′ точки M в повернутой системе K′ дается суммой отрезков Oa и ax′ . Из треугольников ∆Oay и ∆bMy имеем
Oa = Oy sin ϕ = y sin ϕ , ax′ = My cosϕ = xcosϕ .
Аналогично, y′ дается разностью отрезков ay и by , причем ay = Oy cosϕ = y cosϕ , by = My sin ϕ = xsin ϕ .
Таким образом, координаты точки M в системе K′ , повернутой относи- тельно системы K на угол ϕ , даются соотношениями
x′ = xcosϕ + ysinϕ |
|
(а) |
|
ϕ |
|
y′ = −xsinϕ + ycos |
|
Эти формулы описывают преобразование поворота системы координат K → K′ на угол ϕ . Обратное преобразование K′ → K представляет собой поворот системы K′ в противоположном направлении на тот же угол, т.е. на угол − ϕ и описывается формулами
x = x′ cos ϕ − y′ sin ϕ |
. |
(б) |
|
||
y = x′ sin ϕ + y′ cos ϕ |
|
|
5.2.Приведение уравнения линии второго порядка
кканоническому виду.
Лемма 1.: Любое уравнение линии второго порядка
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 ,
52

путем поворота на некоторый угол может быть приведено к уравнению, в ко- тором не будет содержаться слагаемое 2Bxy . При этом угол поворота опре- деляется из соотношения:
ctg2ϕ = A − C
2B
Без доказательства.
Лемма 2.: Любое уравнение линии второго порядка
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0
путем параллельного переноса может быть приведено к уравнению, в кото- ром не будет содержаться слагаемые 2Dx и 2Ey .
Доказательство. Величины сдвига параллельного переноса по осям Ox и Oy определяется выделением полного квадрата из выражений Ax2 + 2Dx и Cy2 + 2Ey , приведенного с помощью поворота декартовой системы коорди- нат (т. е. без слагаемого 2Bxy ) уравнения линии второго порядка:
Ax2 + 2Dx = A x2
Cy2 + 2Ey = C y2
И, следовательно:
|
D |
|
D 2 |
|
+ 2 |
|
x + |
|
|
A |
|
|||
|
|
A |
||
|
E |
|
E 2 |
|
+ 2 |
|
y + |
|
|
C |
|
|||
|
C |
|||
|
D |
2 |
|
|
D |
2 |
|
|
D |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
− |
|
|
|
= A x + |
|
|
|
|
− |
|
|
|
|
и |
||||
|
|
|
|
|
|
A |
||||||||||||
|
A |
|
|
A |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
2 |
|
|
E |
2 |
|
|
E |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
− |
|
|
|
= C y + |
|
|
|
|
|
|
− |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
C |
|||||||||
C |
|
|
C |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|||
x′ = x + |
|
|
|
|
|
|
A . |
||||
|
|
||||
y′ = y + |
E |
|
|||
C |
|||||
|
|
||||
Лемма 3.: Любое уравнение линии второго порядка
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0
путем параллельного переноса и поворота может быть приведено к одному из девяти канонических уравнений:
1)x2 + y2 = 1 - эллипс, a2 b2
2)x2 − y2 = 1 - гипербола, a2 b2
3)y2 = 2px - парабола,
4)x2 + y2 = −1 - мнимый эллипс, a2 b2
53
5)x2 + y2 = 0 - пара мнимых пересекающихся прямых, a2 b2
6)x2 − y2 = 0 - пара действительных пересекающихся прямых, a2 b2
7)x2 − a2 = 0 - пара действительных параллельных прямых,
8)x2 + a2 = 0 - пара мнимых параллельных прямых,
9)x2 = 0 - пара совпадающих действительных прямых.
Пример 1. Привести к каноническому виду кривую x2 + 2y2 +2x - 4y-1=0
Решение. Выделим полные квадраты по переменным x и y :
(x2 + 2x + 1) - 1 + 2(y2 - 2y + 1) - 2 - 1 = 0.
Откуда
|
2 |
|
2 |
|
|
(x + 1)2 |
|
(y − 1)2 |
|
(x + 1) |
|
+ 2(y - 1) |
|
= 4 |
или |
|
+ |
|
= 1 - эллипс. |
|
|
4 |
2 |
||||||
|
|
|
|
|
|
|
|
||
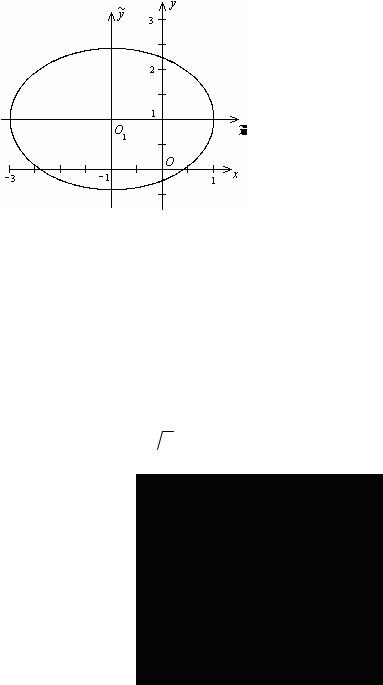
Введем новую систему координат с началом в точке O1(-1; 1), получаю- щуюся из старой параллельным переносом. В новой системе координат эл-
~ |
2 |
~2 |
|||
липс задается уравнением |
x |
|
+ |
y |
= 1, а это — каноническое уравнение |
|
|
|
|||
4 |
2 |
|
|||
эллипса с полуосями 2 и  2 (рис. 5.3.).
2 (рис. 5.3.).
Рис. 5.3.
Пример 2. Привести к каноническому виду кривую xy = 2 .
Решение. Так как A = C = 0 , то ctg 2ϕ = 0, откуда ϕ = 45o . Тогда фор- мулы перехода имеют вид:
54
|
1 |
(x′ − y′) |
x = x′ cos ϕ − y′ sin ϕ = |
2 |
|
|
. |
|
|
1 |
|
|
(x′ + y′) |
|
y = x′ sin ϕ + y′ cos ϕ = |
2 |
|
|
|
Подставляя в данное по условию уравнение, имеем:
(x′ − y′)(x′ + y′) |
= 2 или |
x′2 |
y′2 |
|||
|
|
− |
|
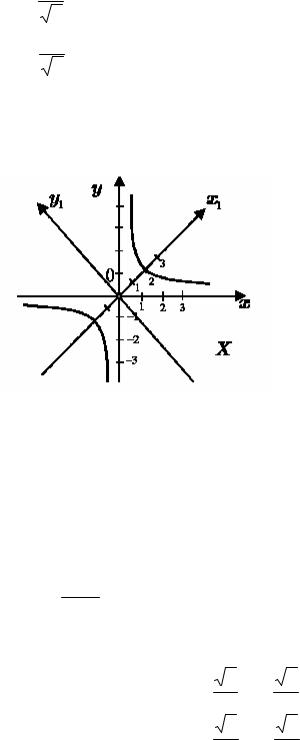
= 1 − равносторонняя гипербола, |
||
2 |
4 |
4 |
||||
|
|
|
||||
асимптотами которой являются оси OX и OY (рис. 5.4.).
Рис. 5.4.
Пример 3. Привести к каноническому виду уравнение
3x2 + 4xy + 3y 2 + 8x + 12y + 1 = 0 .
Решение.
Избавляемся от слагаемого со смешанным произведением переменных. Для этого вычисляем угол поворота:
ctg2ϕ = 3 − 3 = 0, 2ϕ = 90° , ϕ = 45° .
4
Следовательно, формулы для замены координат будут выглядеть следую- щим образом:
x |
|
x′ cos45 |
y′ sin 45 |
x′ 2 |
|
y′ 2 |
||
|
= |
° − |
° = |
|
2 |
− |
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
2 |
|
|
= x′ sin 45° + y′ cos45° = x′ |
+ y′ |
||||||
y |
2 |
2 |
||||||
|
|
|
|
|
|
|
||
Подставляем в уравнение вместо x и y, и приводим подобные слагаемые:
55

3 (x′ − y′)2 + 4 |
(x′ − y′)(x′ + y′) + 3 |
(x′ + y′)2 + 4 |
2(x′ − y′) + 6 |
2(x′ + y′) + 1 = 0 |
|||||||||||||||
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
− 3x′y′ + |
3 |
y′ |
2 |
+ 2x′ |
2 |
− 2y′ |
2 |
+ |
3 |
|
2 |
+ 3x′y′ + |
3 |
y′ |
2 |
+ |
|
x′ |
|
2 |
|
|
|
x′ |
|
2 |
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
4  2x′ − 4
2x′ − 4  2y′ + 6
2y′ + 6  2x′ + 6
2x′ + 6  2y′ + 1 = 0 5x′2 + y′2 + 10
2y′ + 1 = 0 5x′2 + y′2 + 10 2x′ + 2
2x′ + 2  2y′ + 1 = 0
2y′ + 1 = 0
Теперь необходимо избавиться от линейных слагаемых, для этого выде- ляем полный квадрат:
5x′2 + 10 2x′ = 5(x′2 + 2
2x′ = 5(x′2 + 2  2x′ + 2 − 2) = 5(x′ +
2x′ + 2 − 2) = 5(x′ +  2)2 − 10 y′2 + 2
2)2 − 10 y′2 + 2 2y′ = y′2 + 2
2y′ = y′2 + 2  2y′ + 2 − 2 = (y′ +
2y′ + 2 − 2 = (y′ +  2)2 − 2
2)2 − 2
И, следовательно, имеем:
5(x′ +  2)2 − 10 + (y′ +
2)2 − 10 + (y′ +  2)2 − 2 + 1 = 0
2)2 − 2 + 1 = 0
Из этого уравнения получаем величины сдвигов для параллельного перено- са.
x′′ = x′ + |
2 |
|
. |
y′′ = y′ + |
2 |
Окончательно получаем:
5x′′2 + y′′2 = 11
Приводя к форме канонического уравнения, имеем:
|
x′′ 2 |
+ |
y′′ 2 |
- уравнение эллипса. |
||
|
|
|
|
= 1 |
||
( |
|
5 |
) |
2 |
( 11)2 |
|
11 |
|
|
|
|||
|
|
|
|
|
||
6. Поверхности второго порядка
Определение: Поверхностью второго порядка называют поверхность,
определяемую уравнением второй степени относительно текущих декарто- вых координат х и у, то есть
Ax2 + 2Bxy + Cy2 + 2Dxz + Ez2 + 2Fyz + Kx + Ly + Mz + N = 0 ,
где хотя бы один из коэффициентов A, B, C, D, E, F ≠ 0.
Например, сфера (x-a)2+ +(y-b)2+(z-c)2=R2, является поверхностью второго порядка.
56

6.1. Эллипсоид.
Определение. Эллипсоидом называется поверхность, каноническое уравнение которой в декартовой системе координат имеет вид
x2 |
+ |
y2 |
+ |
z |
2 |
= 1 |
||
a2 |
b |
2 |
c |
2 |
||||
|
|
|
||||||
Отметим свойства эллипсоида, вытекающие из определения:
1. Поверхность симметрична относительно координатных плоскостей и цен-
тра О ― центр эллипсоида.
2
2. Из уравнения получаем, что х2 ≤ 1 х ≤ а . Аналогично у ≤ b и z ≤ c.
а
Таким образом эллипсоид расположен внутри параллелепипеда с центром в точке О и сторонами, равными 2а, 2b, 2c. Числа а, b, c называются по-
луосями эллипсоида.
3.Точки пересечения с осями:
х= у = 0 z = ±c. Аналогично x = ±a и y = ±b . Тогда точки
A1(−a; 0; 0), A2 (a; 0; 0), B1(0; − b; 0), B2 (0; b; 0), C1(0; 0; − c), и C2 (0; 0, c) ― вершины эллипсоида.
Для того, чтобы построить эллипсоид, применим метод параллельных сечений.
Рассечем эллипсоид плоскостью, |
параллельной плоскости Оху: z = h |
||||||||||||||||||||||||||||||||||||||||
(т.к. |
|
|
z |
|
≤ c, |
то |
|
|
h |
|
|
≤ c ). Тогда линия пересечения будет определяться систе- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
y |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
y |
2 |
|
|
2 |
|
|
|
||||||||||
|
|
|
x |
|
+ |
|
|
|
+ |
z |
|
|
= 1 |
x |
|
|
+ |
|
= 1 − h |
|
|
|
|
||||||||||||||||||
|
|
|
|
b2 |
|
|
c2 |
|
|
b2 |
|
|
|
|
|||||||||||||||||||||||||||
мой |
|
|
a2 |
|
|
|
|
|
|
|
|
или |
a2 |
|
|
|
|
c2 . |
|
|
|
||||||||||||||||||||
|
|
|
|
= h |
|
|
|
|
|
|
|
|
|
|
|
|
|
= h |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||||||||||||
Если |
|
h |
|
|
|
|
|
< c , то |
|
1 − h2 |
> 0 . Разделим на 1 − h2 |
, имеем: |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
y |
2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ |
|
|
|
= 1 |
|
|
|
|
|
|
|
|
|
− h |
2 |
|
|
= b 1 − h |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
a |
|
= a |
|
1 |
b |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
, где |
1 |
|
, |
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
c2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z = h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Это уравнение эллипса с полуосями a1 и b1 в плоскости z = h . |
|||||||||||||||||||||||||||||||||||||||||
Заметим, что с уменьшением |
|
h |
|
|
полуоси a1 и b1 увеличиваются. |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
h |
|
|
|
= c , то сечения представляют собой точки С1 и С2 . |
|||||||||||||||||||||||||||||||||||
Если |
|
|
|
||||||||||||||||||||||||||||||||||||||
Если |
|
h |
|
= 0 , т.е. h = 0 эллипс имеет полуоси a и b . |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
Аналогично получим, что сечения эллипсоида плоскостями, параллель- ными плоскостям Оуz и Охz тоже являются эллипсами (рис. 6.1.).
57
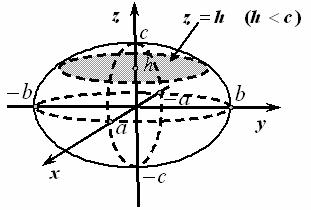
Влюбой плоскости, параллельной координатным плоскостям, мы имеем
всечениях эллипсы, отсюда и название данной поверхности.
Рис.6.1.
Замечания.
1.Если a = b = c , то уравнение эллипсоида примет вид x2 + y2 + z2 = a2 .
Это сфера.
2. |
Уравнение |
(х − х |
0 )2 |
+ |
(у − у |
0 )2 |
+ |
(z − z |
0 )2 |
= 1 определяет эллипсоид с |
|||
а |
2 |
|
b |
2 |
|
c |
2 |
|
|||||
|
|
|
|
|
|
|
|
||||||
центром в точке O′(x0; y0; z0 ).
6.2. Однополостный гиперболоид
Определение. Однополостным гиперболоидом называется поверхность,
каноническое уравнение которой имеет вид
x |
2 |
+ |
y |
2 |
− |
z |
2 |
= 1. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
a2 |
b2 |
c2 |
||||||
Отметим свойства однополостного гиперболоида, вытекающие из опре- деления:
1)т.О ― центр симметрии поверхности;
2)поверхность симметрична относительно координатных плоскостей.
Для того, чтобы построить однополостной гиперболоид, применим ме-
тод параллельных сечений.
В сечениях гиперболоида плоскостью Оуz ( х = 0) имеем гиперболу
|
2 |
|
z |
2 |
|
|
|
y |
|
− |
|
= 1 |
|
|
|
c |
|
|||
b2 |
|
2 |
. |
|||
=х 0
В сечениях гиперболоида плоскостью Охz ( у = 0 ) имеем гиперболу
58

|
|
|
|
2 |
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
− |
|
= 1 |
|
|
|
|
|
|||
|
|
|
|
c2 |
|
|
|
|
|
||||||
|
|
|
a2 |
|
|
|
. |
|
|
|
|
|
|||
|
|
|
у = 0 |
|
z = h , |
|
|
|
|
||||||
Рассечем поверхность |
плоскостями |
|
параллельными плоскости |
||||||||||||
|
|
2 |
|
y |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
x |
|
+ |
|
= 1 |
+ h |
|
|
|
|
|
|
|||
|
|
b2 |
|
|
|
|
|
|
|||||||
Оху. В сечениях имеем линии a2 |
|
|
|
|
c2 . |
|
|
|
|
|
|||||
|
|
= h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||
При h = 0 получим самый маленький эллипс с полуосями a и b ― гор- |
|||||||||||||||
ловой эллипс. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ |
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
||||
При h ≠ 0 получим в сечениях эллипсы a2 |
|
, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
z = h |
|
|
|||
где a1 = a 1 + h2 , b1 = b |
1 + h2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
c2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При увеличении h полуоси эллипса увеличиваются (рис.6.2.).
Рис.6.2.
Замечания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. Уравнения |
x2 |
− |
y2 |
+ |
z2 |
= 1 |
и − |
x2 |
+ |
y2 |
+ |
z2 |
= 1 |
определяют од- |
|
|
|
|
|
||||||||||||
a2 |
b2 |
c2 |
a2 |
b2 |
c2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
нополостные гиперболоиды, направленные вдоль осей Оу и Ох.
2. Если центр гиперболоида находится в точке O′(x0; y0; z0 ), то
(х − х0 )2 |
(у − у0 )2 |
(z − z0 )2 |
|
|||
|
+ |
|
− |
|
= 1 |
― уравнение смещенного гиперболои- |
|
|
|
||||
а2 |
b2 |
c2 |
|
|||
да.
59

6.3. Двуполостный гиперболоид
Определение. Двуполостным гиперболоидом называется поверхность,
каноническое уравнение которой имеет вид
x2 + y2 − z2 = −1. a2 b2 c2
Отметим свойства однополостного гиперболоида, вытекающие из опре- деления:
1)т.О ― центр симметрии поверхности;
2)поверхность симметрична относительно координатных плоскостей.
Для того, чтобы построить двуполостной гиперболоид, применим метод параллельных сечений.
В сечениях гиперболоида плоскостью Оуz ( х = 0) имеем гиперболу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
− |
|
|
|
= −1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В сечениях гиперболоида плоскостью Охz ( у = 0 ) имеем гиперболу |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
− |
|
|
= −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у = 0 |
|
|
|
|
|
z = h , |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рассечем поверхность |
плоскостями |
|
параллельными |
|
плоскости |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
y |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
+ |
|
|
= −1 + h |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Оху. В сечениях имеем линии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
a2 |
|
|
|
b2 |
|
|
|
|
|
c2 . |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z = h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Первое уравнение имеет смысл только при h2 |
− 1 ≥ 0 ,т.е. |
|
h |
|
≥ c . |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При |
|
|
|
h |
|
|
|
|
< c секущая плоскость не пересекает гиперболоид. |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
При |
|
|
h |
|
|
= c получим две точки C1(0; 0; − c) и C2 (0; 0, c). |
|
|
|
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
+ |
|
= 1 |
||
При |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
> c уравнения линий пересечения будут эллипсы a2 |
|
, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
где a1 = a |
|
|
|
|
|
h2 − 1 , b1 = b |
h2 |
− 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = h |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
c2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При увеличении h полуоси эллипса увеличиваются (рис.6.3.).
60
