
учебник(математика)
.pdf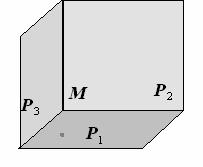
Рис.1.17.
Решение. Координаты точки пересечения плоскостей удовлетворяют ка- ждому из уравнений плоскости, следовательно, решение задачи сводится к
нахождению решения системы трёх алгебраических уравнений:
x + y + z = 3 2x − y − z = 0 .
x + 2y − z = 2
Найдём решение этой системы по формулам Крамера:
x = |
∆ |
x |
, y |
= |
|
∆y |
|
, z |
= |
|
∆ |
z |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Имеем ∆ = |
1 |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
1 |
|
|
1 |
= 3 (− 1)2 +1 |
|
1 |
1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|
− 1 |
− 1 |
= |
3 |
0 |
|
|
0 |
|
|
= 9 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
− 1 |
|
|
|
1 |
2 |
|
|
|
|
− 1 |
|
|
|
|
|
|
|
2 |
|
− 1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
1 |
1 |
|
|
|
3 |
|
|
0 |
0 |
|
= 3 (− 1)1+1 |
|
− 1 |
− 1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
∆ x = |
|
|
|
0 − 1 |
|
− 1 |
= |
|
0 − 1 − 1 |
|
|
= 9 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
− 1 |
|
|
|
|
2 |
|
|
2 |
− |
1 |
|
|
|
2 |
|
|
|
− 1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
3 |
|
1 |
|
|
|
|
3 |
|
|
3 |
0 |
|
= (− 1) (− 1)2+3 |
|
3 |
3 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
∆ y = |
|
|
2 0 − 1 |
|
= |
2 0 − 1 |
|
|
= 9 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
− 1 |
|
|
|
− 1 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
− 1 |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
3 |
|
|
|
|
3 |
|
|
0 |
3 |
|
= (−1) (−1)2+ 2 |
|
3 3 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
∆ z = |
|
2 −1 0 |
|
= |
2 −1 0 |
|
|
= 9 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
2 |
2 |
|
|
|
|
5 |
|
|
0 |
2 |
|
|
|
|
5 |
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Окончательно получим |
|
x = 1; |
|
y = 1; z = 1. Итак, точка пересечения плос- |
||||||||||||||||||||||||||||||||||||||||||||
костей M (1,1,1).
Пример 4. Найти уравнение плоскости, проходящей через точку M 0 (1,−1,−1) и линию пересечения плоскостей (рис.1.18.)
P1 :x + y + z − 3 = 0 и P2 : 2x + y − z − 2 = 0 .
Решение. Возьмём на линии пересечения плоскостей две какие-нибудь (любые) различные точки M 1(x1,y1,z1 ) и M 2 (x 2 ,y 2 ,z 2 ) так, чтобы координа- ты этих точек удовлетворяли системе двух уравнений, полученной из урав- нений плоскостей.
11

Рис.1.18.
Эта система содержит два уравнения с тремя неизвестными, значит она имеет бесчисленное множество решений (это есть множество точек, лежащих на линии пересечения плоскостей l ). Зафиксируем в этой системе перемен- ную z , положив, например, z1 = 0 , тогда получим
x1 + y1 |
= 3 |
|
= −1, y1 |
= 4 . |
|
=> x |
1 |
||
2x1 + y1 = 2 |
|
|
|
|
Итак, мы нашли точку M 1(−1,4,0) . Положим теперь z 2 = 1, тогда имеем:
x 2 + y 2 |
= 2 |
2 = 1, y 2 |
= 1. |
||||
2x 2 + y |
|
=> x |
|||||
2 = 3 |
|
|
|||||
Получим вторую точку M 2 (1,1,1). Введём в рассмотрение векторы |
|||||||
uuuuuuur |
|
|
|
|
uuuuuuuur |
|
|
M 0M 1 = −2i + |
5j + k , |
M 0M 2 = 2j + 2k . Теперь можно найти нормаль к иско- |
|||||
|
|
|
|
|
|
uuuuuuur |
uuuuuuuur |
мой плоскости P : n = M 0M 1 |
× M 0M 2 , |
||||||
|
i |
j |
k |
|
|
|
|
|
|
|
|
||||
n = |
−2 5 1 |
|
= 8i + 4j − 4k . |
||||
|
0 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Сокращая на 4, возьмём более простое выражение для нормали
n = 2i + j − 2k . Теперь остаётся написать уравнение искомой плоскости P :
P : 4(x − 1) + 1(y + 1) − 2(z + 1) = 0
Окончательно общее уравнение искомой плоскости: 2x + y − z − 2 = 0 .
Пример 5. Вычислить высоту hS пирамиды с вершинами в точках : S ( 0, 6, 4 ) , A ( 3, 5, 3 ) , B ( -2, 11, -5 ) , C ( 1, -1, 4 ) .
Решение: Запишем уравнение грани ABC :
x − 3 |
y − 5 |
z − 3 |
|
= 2x - y - 2z + 5 = 0 |
|
||||
− 2 − 3 11 − 5 − 5 − 3 |
|
|||
1 − 3 |
− 1 − 5 |
4 − 3 |
|
|
Найдем расстояние от точки S ( 0, 6, 4 ) до плоскости 2x – y - 2z + 5=0 :
12
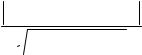
hs = 2 0 − 6 − 2 4 + 5 = 3.  22 + 12 + 22
22 + 12 + 22
1.6.Контрольные вопросы к § 1.
1.Что называется уравнением поверхности в пространстве? Приведите при- меры поверхностей.
2.Дайте определение нормального вектора плоскости.
3.Как связаны между собой нормальные векторы двух плоскостей, если эти плоскости:
а) параллельны; б) перпендикулярны?
4.Выведите уравнение плоскости, проходящей через данную точку и имею- щей данный нормальный вектор.
5.Каков геометрический смысл коэффициентов при неизвестных в общем уравнении плоскости?
6.Какие частные случаи общего уравнения плоскости называются неполны- ми уравнениями плоскости? Приведите примеры.
7.Выведите уравнение плоскости, проходящей через три данные точки.
8.Сформулируйте и докажите условия параллельности и перпенди- кулярности плоскостей.
9.Выведите формулу для вычисления косинуса угла между плоскостями.
10.По какой формуле находится расстояние от данной точки до плоскости?
|
|
§ 2. Прямая линия в пространстве |
Линию L |
в пространстве будем рассматривать как пересечение двух |
|
поверхностей S1 |
и S2 , то есть геометрическое место точек, находящихся |
|
одновременно на двух поверхностях |
||
|
|
F1 ( x, y, z ) = 0 и F2 ( x, y, z ) = 0 , |
то есть |
L = S1 ∩ S2 F1(x;y;z) = 0 . |
|
|
|
F2(x;y;z) = 0 |
Например, окружность x2 + y2 = 16 , получающаяся пересечением сфе- ры x2+y2+z2=16 плоскостью z = 0 , определяется системой уравнений:
|
2 2 |
2 |
|
+ y |
+ z = 16 . |
x |
||
|
= 0 |
|
z |
|
13
2.1. Общее уравнение прямой в пространстве
Прямую линию L в пространстве можно рассматривать как пере- сечение двух различных и непараллельных плоскостей Р1 и Р2 .
L = Р1 |
∩ Р2 |
A1x + B1y + C1z + D1 = 0 |
(2.1) |
|
|
A2x + B2y + C2z + D2 = 0 |
|
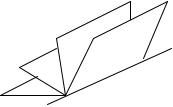
Уравнения (2.1) называют общими уравнениями прямой L . Уравне- ний типа (2.1), определяющих одну и ту же прямую L , бесконечное мно- жество, так как через прямую L можно провести бесконечное множество плоскостей (рис. 2.1).
L
Р2 Р1
Р3
Р4 •M0(x0, y0, z0 )
Рис. 2.1
Множество всех плоскостей, проходящих через заданную прямую L,
называется пучком плоскостей, прямая L — осью пучка.
Заметим, что уравнение
A1x + B1y + C1z + D1 + λ ( A2x + B2y + C2z + D2 ) = 0 , (2.2)
где λ - параметр, при различных λ дает уравнение любой плоскости пучка, ось которого задана уравнением (2.2), кроме плоскости Р2 :
A2x+B2y+C2z+D2=0.
Уравнение (2.2) пучка плоскостей используется при решении задач, в кото- рых требуется провести плоскость через заданную прямую, причем значение λ находится из какого-либо дополнительного условия.
Если (2.2) переписать в виде
1/λ ( A1x + B1y + C1z + D1 ) + ( A2x + B2y + C2z + D2 ) = 0 ,
то Р2 получается как предельное значение при λ → ∞ .
2.2. Векторное уравнение прямой в пространстве
Положение прямой линии в пространстве можно задать различными спо- собами. В частности, через данную точку M 0 (x 0 ,y 0 ,z 0 ) параллельно данно- му ненулевому вектору S(m ,n ,p ) можно провести единственную прямую
(рис. 2.2.).
14
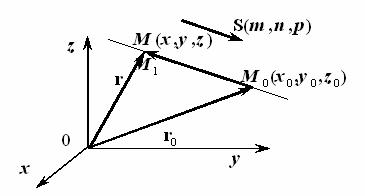
Рис.2.2.
Вектор S называется направляющим вектором прямой. Обозначим через
r0 радиус-вектор точки M 0 , а через r |
- радиус-вектор произвольной точки |
|
M , лежащей на прямой. |
|
|
uuuuuuur |
uuuuuuur |
= r − r0 , следо- |
Очевидно, что векторы M 0M и S коллинеарны, но M 0M |
||
вательно r − r0 = λS . Отсюда |
|
|
r = r0 + λS |
(2.3).) |
|
Уравнение (2.3) называется векторным уравнением прямой линии в про- странстве.
2.3. Параметрические и канонические уравнения прямой
Запишем уравнение (2.3) в виде:
xi + y j + z k = x0i + y 0 j + z 0k + λm i + λn j + λpk = (x0 +λm )i +(y0 +λn)j+(z0 +λp)k
Примем теперь во внимание, что если два вектора равны, то совпадают их координаты в данном базисе i , j, k :
x = x 0 |
+ λm |
|
|
y = y |
|
|
(2.4) |
0 |
+ λn |
||
z = z |
|
|
|
0 |
+ λp |
|
|
Уравнения (2.4) называются параметрическими уравнениями прямой.
Здесь в качестве параметра выступаетλ . Придавая λ различные числовые значения из (−∞,+∞) , будем получать на прямой различные точки.
Исключая из уравнения (2.4) параметр λ , получим так называемые кано-
нические уравнения прямой:
x − x 0 |
= |
y − y 0 |
= |
z − z 0 |
. |
(2.5) |
m |
n |
|
||||
|
|
p |
|
|||
Эти уравнения называют каноническими уравнениями прямой L ,
проходящей через точку M0(x0,y0,z0) и имеющeй направляющий вектор
v
S ={m,n,p}.
15
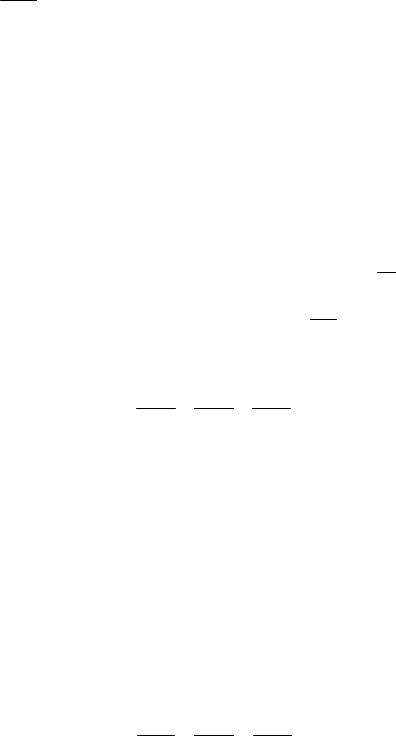
Очевидно, уравнения (2.5) представляют собой условия коллинеарнос-
v
ти векторов M0M = { x-x0 , y-y0 , z-z0 } и S = { m, n, p }.
Кроме того, канонические уравнения (2.5) представляют систему двух уравнений
x − x 0 |
= |
y − y 0 |
, |
|||
|
|
|
|
|||
m |
n |
|||||
|
|
|
||||
|
x − x 0 |
|
z − z 0 |
|
|
|
|
= |
|
, |
|||
|
m |
p |
||||
|
|
|
||||
определяющих соответственно две плоскости Р1 и Р2 , пересечение которых дает прямую L , проходящую через точку M0(x0,y0,z0) имеющую на-
v
правляющий вектор S = { m, n, p }.
Пример 1. Даны точки А(-1,2,3) и В(2,-3,1). Составить уравнения пря-
мой, проходящей через M0(3,-1,2) и параллельной вектору AВ.
Решение: По условию дана точка M0 (3 ,-1,2), то есть x0=3, y0=-1, z0=2.
v
В качестве направляющего вектора возьмем S= AB ={3,-5,-2}, то есть m =3, n = -5, p = -2.
Используя (2.5), запишем канонические уравнения прямой:
L : x − 3 = y + 1 = z − 2 (= t). |
||
3 |
− 5 |
− 2 |
Приравняв все части равенства параметру t , получим параметрические уравнения прямой:
x = 3t + 3
= − −
L : y 5t 1 .
z = −2t + 2
Пример 2. Написать канонические и параметрические уравнения пер- пендикуляра L к плоскости Р : 2x - 3y + z - 7 = 0 , проходящего через точку
M0 ( -1, 2, 3 ).
Решение: По условию x0 = -1, y0 =2, z0 =3. В качестве направляющего
v |
|
|
вектора возьмем вектор S= { 2, -3, 1 } Р . Тогда каноническое уравнение |
||
перпендикуляра имеет вид: |
|
|
L : x + 1 = y − 2 = z − 3 (= t). |
||
2 |
− 3 |
1 |
Приравняв все части последнего равенства параметру t, получим иско- мое параметрические уравнения прямой:
x = 2t − 1
= − +
L : y 3t 2
z = t + 3
16
Пример 3. Приведем к каноническому виду уравнения прямой
L = Р1 |
∩ Р2 |
2x |
+ 3y − 16z − 7 = 0 . |
|
|
3x |
+ y − 17z = 0 |
Решение: Требуется записать канонические уравнения этой прямой L (рис. 2.3), для чего необходимо знание точки M0(x0,y0,z0) L и направляюще-
го вектора S || L. Координаты точки M0(x0,y0,z0) находятся из заданной сис- темы при произвольном значении одной из координат.
l |
• M0(x0, y0, z0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
N1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
v |
v |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = N1 × N2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис 2.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно взять векторное произве- |
||||||||||||||||||||||
|
В качестве направляющего вектора |
S |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Р1 |
|
|
|
|
|
Р2 , то есть |
|
|
|
= |
|
1 × |
|
2 . |
|
|
|
|
||||||||||||||
дение векторов |
n1 |
и |
n1 |
S |
n |
n |
|||||||||||||||||||||||||||||||||||
Найдем M0(x0,y0,z0) L. Пусть z0 =0, тогда для нахождения x0 и y0 полу- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2x0 + 3y0 |
= 7 |
|
, решая которую, найдем x0 = -1 и y0 = 3 , то есть |
||||||||||||||||||||||||||||||||
чаем систему |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3x0 + y0 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
M0 ( -1, 3, 0 ). |
|
|
|
= {2,3,-16} Р1, и |
|
|
|
={3,1,-17} Р2, поэтому |
|||||||||||||||||||||||||||||||||
Из условия задачи |
|
n1 |
n2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i |
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
1 × |
|
2 = |
2 |
3 |
|
− 16 |
= −35i − 14j − 7k . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
S |
n |
n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
3 |
1 |
|
− 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 = − |
1 |
|
|
= { 5; 2; 1}. |
|||||||||||||||||||||||||||||
В качестве направляющего вектора возьмем |
S |
S |
|||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
||||||
Итак, искомые канонические уравнения прямой |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
L : |
x + 1 |
= |
y − 3 |
= |
z − 0 |
(= t). |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
2.4. Уравнение прямой, проходящей через две данные точки
Пусть даны две различные точки M 1(x1,y1,z1 ) и M 2 (x 2 ,y 2 ,z 2 ). Очевидно, что через эти две точки можно провести единственную прямую (рис.2.4.). В
17

= uuuuuuur
качестве направляющего вектора этой прямой возьмём вектор S M 1M 2 , а в качестве фиксированной точки можно взять любую из точек M 1 или M 2 .
Рис.2.4.
Пусть это будет точка M 1 . Тогда канонические уравнения прямой, про- ходящей через две данные точки, имеют вид
x − x1 = y − y1 = z − z1 . x 2 − x1 y 2 − y1 z 2 − z1
Пример 1. Найти параметрические уравнения прямой, проходящей через точки M1(2,-5,1) и M2(-1,1,2).
Решение. В качестве точки М0 можно взять любую из двух данных то- чек, пусть для определения М0 =M1. За направляющий вектор возьмем
v |
= { x2 − x1 , y2 − y1 , z2 − z1 } = { − 3; 6; 1 }. |
||||||||
S = |
|
||||||||
M1M2 |
|||||||||
|
|
14243 |
14243 |
123 |
|||||
|
|
|
m |
|
n |
p |
|||
Запишем каноническое уравнение прямой: |
|||||||||
|
|
L : |
x − 2 |
= |
y + 5 |
= |
z − 1 |
(= t), |
|
|
|
|
|
1 |
|||||
x = −3t + 2 |
|
− 3 |
6 |
|
|
||||
|
|
|
|
|
|
|
|
||
откуда L : y = 6t − 5 |
и есть искомые параметрические уравнения. |
||||||||
z = t + 1
2.5. Угол между двумя прямыми. Взаимное расположе- ние двух прямых в пространстве
Определение. Углом между двумя прямыми называется наименьший угол между их направляющими векторами.
Очевидно, что если
l1 |
: |
x − x1 |
= |
y − y1 |
= |
z − z1 |
и l2 |
: |
x − x 2 |
= |
y − y 2 |
= |
z − z 2 |
, |
m 1 |
n1 |
p1 |
|
n 2 |
|
|||||||||
|
|
|
|
|
|
m 2 |
|
p2 |
||||||
то угол ϕ между прямыми l1 и l2 можно вычислить из соотношения
cosϕ = |
|
S1 |
S2 |
= |
m 1m 2 |
+ n1n 2 |
+ p1p2 |
. |
||||||
|
S1 |
|
|
|
|
S 2 |
|
|
m 12 + n12 + p12 m 22 + n 22 + p22 |
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||
18
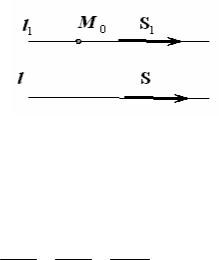
1) Если прямые l1 и l2 параллельны, то их направляющие векторы S1 и S2 коллинеарны, следовательно, условие параллельности двух прямых имеет вид:
m 1 |
= |
n1 |
= |
p1 |
|
m 2 |
n 2 |
p2 |
|||
|
|
2) Если прямые l1 и l2 перпендикулярны, то S1 S2 = 0 , следовательно, усло- вие перпендикулярности двух прямых имеет вид:
m 1m 2 + n1n 2 + p1p2 = 0
Заметим, что в силу рассмотренных ранее теорий полученные условия являются необходимыми и достаточными условиями соответственно парал- лельности и перпендикулярности двух прямых в пространстве.
Пример 1. Найти канонические уравнения прямой, проходящей через
точку M 0 |
(1,−1,2) и параллельной данной прямой l : |
x + 1 |
= |
y − 1 |
= |
z |
|
|
−1 |
||||
|
2 |
|
−1 |
|||
(рис.2.5.).
Решение.
Рис.2.5.
Направляющий вектор данной прямой l есть S = 2i − j − k .
Искомая прямая l1 параллельна данной прямой l , значит её направляю- щий вектор S1 = S . Фиксированная точка M 0 (1,−1,2) лежит на искомой. Её
канонические уравнения: x − 1 = y + 1 = z − 2 . 2 −1 −1
Пример 2. Найти канонические уравнения прямой, проходящей через точку M 0 (1,0,−1) и перпендикулярной к двум данным прямым
l |
|
: |
x |
= |
y − 1 |
= |
z + 1 |
|
и |
l |
|
: |
x − 1 |
= |
y + 1 |
= |
z |
(рис.2.6.). |
1 |
|
|
−1 |
2 |
−1 |
|
|
|||||||||||
|
1 |
2 |
|
|
|
|
1 |
1 |
|
|||||||||
Решение.
19

Рис.2.6.
В качестве направляющего вектора искомой прямой l возьмём вектор
|
i |
j |
|
k |
|
|
S = S1 × S2 = |
1 |
2 |
−1 |
= 3i + 3k . За направляющий вектор возьмём коллине- |
||
|
−1 |
1 |
1 |
|
||
арный вектор S1 |
= |
1 |
S = (1;0;1) . Канонические уравнения прямой l : |
|||
3 |
||||||
|
|
|
|
|
||
x− 1 = y = z + 1 .
10 1
2.6.Взаимное расположение прямой и плоскости в про-
странстве
Определение. Углом между прямой и плоскостью называется угол ме-
жду прямой и её проекцией на эту плоскость. (рис. 2.7.)
Рис.2.7.
Пусть плоскость P задана общим уравнением A x + B y +C z + D = 0 , сле-
довательно, нормаль к ней n = (A ,B ,C ). |
|
|
|
|
|
|
Прямая задана каноническими уравнениями |
x − x0 |
= |
y − y 0 |
= |
z − z 0 |
, по- |
m |
n |
|
||||
|
|
|
p |
|||
этому направляющий вектор прямой S = (m ,n ,p ) .В силу определения, если ϕ - угол между прямой и плоскостью, то
20
