Свойства функции распределения

1) 0≤ F(x) ≤1;

2) F(x)  неубывающая функция на промежутке (∞;+∞);

3) F(x)  непрерывна слева в точках х= x_i (i=1,2,…n) и непрерывна во всех остальных точках;

4) F(∞)=Р (Х<∞)=0 как вероятность невозможного события Х <∞, F(+∞)=Р(Х<+∞)=1 как вероятность достоверного события Х <+∞.

Если закон распределения дискретной случайной величины Х задан в виде таблицы:

x	x1	x2	х3	…	хn
p	р1	р2	р3	...	рn

то функция распределения F(x) определяется формулой:

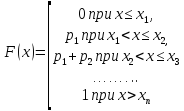
Её график изображен на рис. 4.2:

Рис. 4.2

Числовые характеристики дискретной случайной величины

Определение 5. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности:

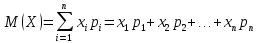
Математическое ожидание характеризует среднее значение случайной величины.

Свойства математического ожидания

1) M(C)=C, где С  постоянная величина;

2) М(СХ)=СМ(Х),

3) М(Х±Y)=М(Х) ±M(Y);

4) M(XY)=M(X)M(Y), где X,Y  независимые случайные величины;

5) M(X±C)=M(X)±C, где С  постоянная величина.

Для характеристики степени рассеяния возможных значений дискретной случайной величины вокруг ее математического ожидания служит дисперсия.

Определение 6. Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

D(X)=M(XM(X))²

Свойства дисперсии

1) D(C)=0, где С  постоянная величина;

2) D(X)>0, где Х  случайная величина;

3) D(C · X)=C²·D(X), где С  постоянная величина;

4)D(X+Y)=D(X)+D(Y), где X,Y  независимые случайные величины;

Для вычисления дисперсии часто бывает удобно пользоваться формулой:

D(X)=M(X²)  (M(X))²,

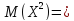
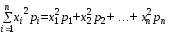
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния возможных значений случайной величины используют также величину.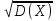

Определение 7. Средним квадратическим отклонением σ(Х) случайной величины Х называется квадратный корень из дисперсии:

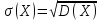
Задача 4.2. Дискретная случайная величина Х задана законом распределения:

х	1	0	1	2	3
р	0,1	p2	0,3	0,2	0,3

Найти p₂, функцию распределения F(x) и построить её график, а также M(X),D(X), σ(Х).

Решение: Так как сумма вероятностей возможных значений случайной величины Х равна 1, то

Р₂=1 (0,1+0,3+0,2+0,3)=0,1

Найдем функцию распределения F(х)=P(X < x).

Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Если х ≤ 1, то F(х)=0, так как на промежутке ( ∞; х) нет ни одного значения данной случайной величины;

Если 1< х ≤0, то F(х) = Р(Х = 1) = 0,1, так как в промежуток (∞; х) попадает только одно значение x₁ = 1;

Если 0 < х ≤ 1, то F(х) = Р(Х = 1) + Р(Х = 0) = 0,1 + 0,1 = 0,2, так как в промежуток (∞; х) попадают два значения x₁ = 1 и x₂ = 0;

Если 1< х ≤2, то F(х)=Р(Х = 1) + Р(Х = 0)+ Р(Х = 1)= 0,1+0,1+0,3=0,5, так как в промежуток (∞; х) попадают три значения

x₁=1, x₂=0 и x₃=1;

Если 2 < х ≤ 3, то F(х) = Р(Х = 1) + Р(Х = 0) + Р(Х = 1) + Р(Х = 2) = =0,1+0,1+0,3+0,2=0,7, так как в промежуток (∞; х) попадают четыре значения x₁ = 1, x₂ = 0, x₃ = 1 и х₄ = 2;

Если х > 3, то F(х)=Р(Х = 1)+Р(Х = 0)+Р(Х = 1)+Р(Х = 2)+Р(Х = 3) = =0,1+0,1+0,3+0,2+0,3=1, так как в промежуток (∞; х) попадают пять значений x₁= 1, x₂ = 0, x₃ = 1, х₄ = 2 и х₅ = 3.

Итак,

Изобразим функцию F(x) графически (рис. 4.3):

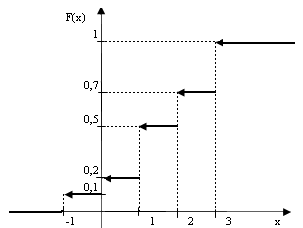
Рис. 4.3

Найдем числовые характеристики случайной величины:

=
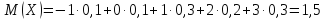
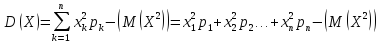
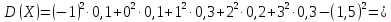
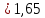
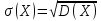