- •Оглавление
- •Задачи с решениями
- •§2. Случайные события и их классификация. Алгебра событий. Вероятность события. Теоремы сложения и умножения вероятностей Случайные события
- •Вероятность события
- •Теоремы сложения и умножения вероятностей
- •Задачи с решениями
- •§3. Формула полной вероятности. Повторные испытания. Формула Бернулли Формула полной вероятности
- •Повторные испытания. Формула Бернулли
- •Формулы Лапласа
- •Формула Пуассона
- •Задачи с решениями
- •Глава 2. Случайные величины §4. Дискретная случайная величина Понятие случайной величины. Закон распределения дискретной случайной величины
- •Фунция распределения
- •Свойства функции распределения
- •Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания
- •Свойства дисперсии
- •Некоторые законы распределения дискретной случайной величины
- •§5. Непрерывная случайная величина Понятие непрерывной случайной величины. Функция распределения непрерывной случайной величины
- •Свойства функции распределения
- •Функция плотности распределения вероятностей
- •Свойства функции плотности распределения вероятностей
- •Числовые характеристики непрерывной случайной величины
- •§6. Некоторые законы распределения непрерывной случайной величины Равномерный закон распределения
- •Показательный (экспоненциальный) закон распределения
- •Нормальный закон распределения
- •"Правило трех сигм"
- •Глава 3. Элементы математической статистики §7. Статистическое распределение выборки Задачи математической статистики
- •Генеральная и выборочная совокупности
- •Статистическое распределение выборки. Полигон и гистограмма
- •Свойства функции (х)
- •Задачи с решениями
- •§8. Статистические оценки параметров Точечные статистические оценки параметров распределения
- •Интервальные оценки параметров нормального распределения
- •Задачи с решениями
- •§9. Проверка статистических гипотез Статистические гипотезы
- •Проверка гипотез
- •Сравнение двух дисперсий нормальных генеральных совокупностей
- •Сравнение нескольких дисперсий нормальных генеральных совокупностей
- •Сравнение двух средних нормальных генеральных совокупностей
- •Задачи с решениями
- •§10. Критерий согласия Пирсона Проверка гипотезы о нормальном распределении
- •Задачи с решениями
- •§11. Элементы теории корреляции
- •Коэффициент корреляции
- •Свойства коэффициента корреляции
- •Проверка значимости выборочного коэффициента корреляции
- •Линейная корреляция. Уравнение регрессии
- •Ранговая корреляция
- •Правило проверки наличия связи между качественными признаками
- •Приложение 1 Контрольные работы и контрольные вопросы по теории
- •Элементы теории вероятностей
- •Элементы математической статистики
- •3. Контрольные вопросы по теории
- •Приложение 2 Вероятностные таблицы
- •Значения функции
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения f Фишера – Снедекора
§6. Некоторые законы распределения непрерывной случайной величины Равномерный закон распределения
Определение 1. Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т.е.

График функции f(x) изображен на рис. 6.1.
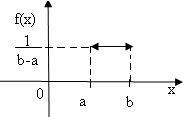
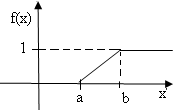
Рис. 6.1 Рис. 6.2
Функция распределения случайной величины Х, распределенной по равномерному закону, задается формулой:
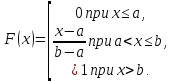
Ее график изображен на рис. 6.2.
Числовые характеристики случайной величины, равномерно распределенной на интервале (a;b), вычисляются по формулам:
M(X)
= ,D(X)
=
,D(X)
=
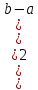 ,
, .
.
Задача 6.1. Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:
а) плотность распределения вероятностей f(x) и построить ее график;
б) функцию распределения F(x) и построить ее график;
в) M(X), D(X), σ(Х).
Решение: Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:
Построим ее график (рис. 6.3):
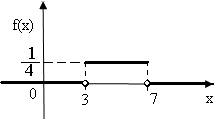
Рис. 6.3
б)
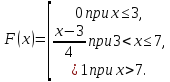
Построим ее график (рис. 6.4):
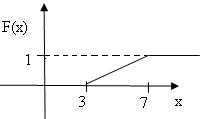
Рис. 6.4
в)
M(X)
=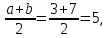 D(X)
=
D(X)
=
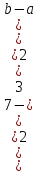
Показательный (экспоненциальный) закон распределения
Определение 2. Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ > 0, если функция плотности распределения вероятностей имеет вид:

Функция распределения случайной величины Х, распределенной по показательному закону, задается формулой:
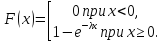
Кривая
распределения f(х)
и график функции распределения F(х)
случайной величины Х
приведены на рис. 6.5 и рис. 6.6. 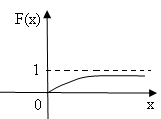
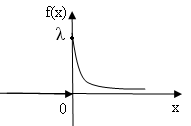
Рис. 6.5 Рис. 6.6
Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны:
M(X)
=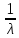 ,D(X)=
,D(X)=
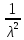 ,
,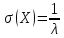 .
.
Таким образом, математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
Вероятность попадания Х в интервал (a;b) вычисляется по формуле:
Р(a
< Х
< b)=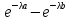 ,
если
(a;b)
,
если
(a;b)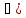
Задача 6.2. Среднее время безотказной работы прибора равно 100 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) плотность распределения вероятностей;
б) функцию распределения;
в) вероятность того, что время безотказной работы прибора превысит 120 ч.
Решение.
По
условию математическое ожидание M(X)
=
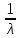 = 100, откудаλ
=
1/100 = 0,01.
= 100, откудаλ
=
1/100 = 0,01.
Следовательно,
б)
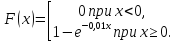
в) Искомую вероятность найдем, используя функцию распределения:
Р(X
>120)
= 1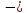 F(120)
=1
F(120)
=1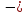 (1
(1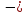 е1,2)
= е1,2
≈
0,3.
е1,2)
= е1,2
≈
0,3.
Нормальный закон распределения
Определение 3. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса), если ее плотность распределения имеет вид:
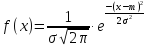 ,
,
где m = M(X), σ2= D(X), σ > 0.
Кривую нормального закона распределения называют нормальной или гауссовой кривой (рис. 6.7).

Рис. 6.7
Нормальная
кривая симметрична относительно прямой
х
= m,
имеет максимум в точке х
= m,
равный
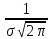 .
.
Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:
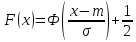 ,
,
Ф(x) – функция Лапласа.
– функция Лапласа.
Замечание. Функция Ф(х) является нечетной (Ф(х) = Ф(х)), кроме того, при х > 5 можно считать Ф(х) ≈ 1/2.
Таблица значений функции Ф(х) приведена в приложении (табл. П 2.2).
График функции распределения F(x) изображен на рис. 6.8.
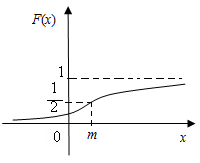
Рис. 6.8
Вероятность того, что случайная величина Х примет значения, принадлежащие интервалу (a;b) вычисляются по формуле:
Р
(a
< Х
<
b)
= .
.
Вероятность того, что абсолютная величина отклонения случайной величины от ее математического ожидания меньше положительного числа δ вычисляется по формуле:
P(|X
m|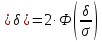 .
.
В частности, при m=0 справедливо равенство:
P(|X|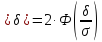 .
.