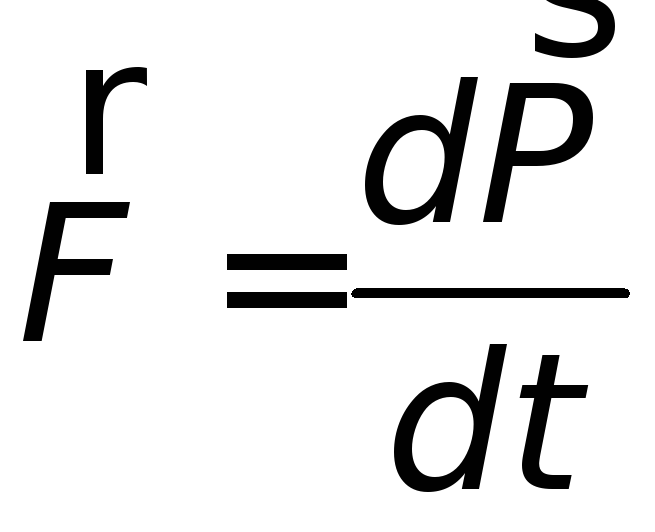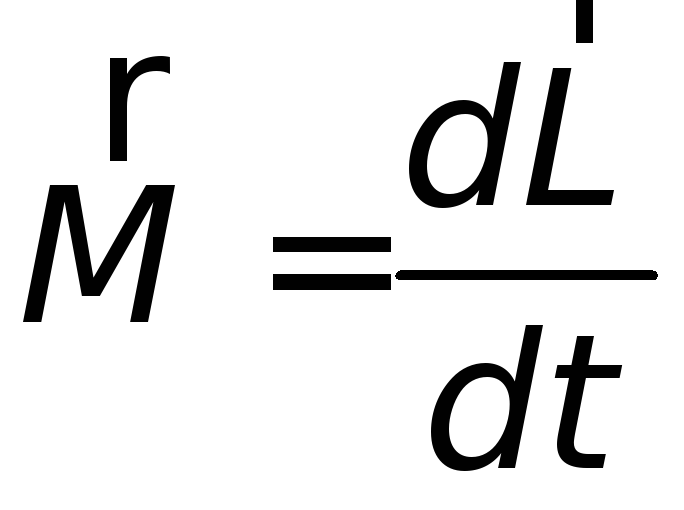- •Динамика материальной точки и твердого тела
- •Оглавление
- •Введение
- •Расчет погрешностей и представление результатов измерений Типы погрешностей
- •Расчет погрешностей при прямых измерениях
- •Расчет погрешностей при косвенных измерениях
- •Как правильно округлить и записать результат
- •Как строить графики
- •Контрольные вопросы
- •Литература
- •Простейшие измерительные приборы Штангенциркуль
- •Микрометр
- •Вращение твердого тела вокруг неподвижной оси
- •Литература
- •Лабораторные работы
- •Определение плотности твердого тела
- •Краткая теория и описание метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Исследование основного закона динамики вращательного движения с помощью маятника обербека
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение момента инерции махового колеса
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение momehта инерции стержня методом крутильных колебаний
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение момента инерции физического маятника
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Приложение (вывод периода колебаний физического маятника)
- •Литература
- •Исследование основного закона динамики вращательного движения с помощью маятника обербека
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение радиуса кривизны вогнутой поверхности методом катающегося шарика
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Изучение удара шаров
- •Краткая теория
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение момента инерции тела и момента сил трения в подшипнике
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Изучение прецессионного движения гироскопа
- •Описание установки и метода измерений
- •Из рис. 9.2 следует, что
- •Порядок выполнения работы
- •Контрольные вопросы
- •Определение ускорения свободного падения с помощью математического маятника Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Определение ускорения свободного падения с помощью физического маятника Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Работа 1.11 изучение основного закона динамики вращательного движения с помощью маятника обербека
- •Описание установки и метода измерений
- •Основной закон динамики для вращательного движения в данной работе удобно записать в виде
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение скорости полета пули с помощью баллистического крутильного маятника
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Определение коэффициентов трения скольжения и трения качения с помощью наклонного маятника
- •Краткая теория
- •Трение скольжения
- •Трение качения
- •Описание установки и метода измерений
- •Часть 1 Определение коэффициента трения скольжения
- •Часть 2 Определение коэффициента трения качения
- •Контрольные вопросы
- •Литература
- •Изучение зависимости момента инерции тела от распределения его массы относительно оси вращения
- •Свободные оси вращения. Главные оси инерции
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •690059, Владивосток, ул. Верхнепортовая, 50а
Микрометр
Микрометр позволяет повысить точность измерений по сравнению со штангенциркулем на порядок, т. е. еще в 10 раз. Микрометры бывают нескольких типов: для наружных измерений, микрометрический глубиномер и микрометрический нутромер.
Микрометр для наружных измерений изображен на рис. И.4.Для измерения предмет помещают между неподвижным упором1и подвижным торцом микрометрического винта2. Микрометрический винт, жестко связанный с барабаном3, перемещается внутри полого неподвижного цилиндра4. Микрометрический винт имеет шаг 0,5 мм.
О
Рис. И.4 1 2 4 3 5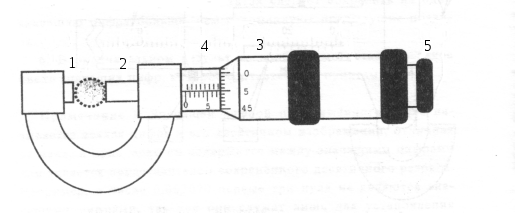
Отсчет производится следующим образом: по горизонтальной шкале цилиндра отсчитывается размер измеряемого предмета с точностью до 0,5 мм. Сотые доли миллиметра отсчитываются по круговой шкале барабана. Причем число сотых долей соответствует делению шкалы, расположенному против продольной черты цилиндра. Полученные результаты складываются.
Внимание! Микрометрический винт необходимо вращать только за трещотку5до возникновения характерного звука. Это предотвращает поломку прибора.
Вращение твердого тела вокруг неподвижной оси
краткая теория к работам
1.1, 1.2, 1.3, 1.4, 1.5, 1.8, 1.9, 1.10, 1.11,1.12, 1.14
В
R О О
Рис. Т.1
![]() и
и
![]() ).
Это значит, что модули их линейных
скоростей
).
Это значит, что модули их линейных
скоростей
![]() и ускорений
и ускорений
![]() различны.
различны.
Движение же тела как
целого можно характеризовать только
такими величинами, которые в данный
момент времени для всех его точек
одинаковы. Поэтому вращательное движение
твердого тела характеризуют не линейными,
а угловыми величинами:
углом поворота
![]()
![]() ,угловой скоростью
,угловой скоростью
![]() иугловым ускорением
иугловым ускорением![]() .
.
Если, вращаясь
равномерно, за промежуток
времени
![]() тело повернулось на угол
тело повернулось на угол
![]() ,
то модуль его
угловой скорости
определится соотношением
,
то модуль его
угловой скорости
определится соотношением
![]() ,
(Т.1)
,
(Т.1)
из которого следует, что угловая скорость численно равна углу, на который тело поворачивается за единицу времени (за одну секунду, одну минуту и т. д.). Если тело вращается неравномерно, то по формуле (Т.1) находят его среднюю угловую скорость.
В тех случаях,
когда известна зависимость угла поворота
от времени, т. е. функция
![]() ,
можно найти мгновенную угловую скорость
как производную от угла поворота по
времени
,
можно найти мгновенную угловую скорость
как производную от угла поворота по
времени
![]() .
(Т.2)
.
(Т.2)
Если тело вращается с постоянным угловым ускорением, то модуль его углового ускорения определяется соотношением
![]() ,
(Т.3)
,
(Т.3)
из
которого видно, что угловое ускорение
численно равно изменению угловой
скорости в единицу времени. В случае
произвольного движения по формуле
(Т.3) находят среднее угловое ускорение.
Мгновенное угловое ускорение можно
найти как производную от угловой скорости
по времени, если известна функция
![]() ,
,
![]() .
(Т.4)
.
(Т.4)
М
Рис. Т.2
![]() ,
,![]() ,
,![]() ,
(Т.5)
,
(Т.5)
где R– радиусы окружностей, по которым движутся точки.
Угол поворота, угловая
скорость и угловое ускорение – величины
векторные (точнее, они являются
псевдовекторами, так как связаны с
направлением вращения тела условно).
Векторы
![]() и
и![]() направлены вдоль оси вращения и связаны
с направлением вращения правилом правого
винта (рис. Т.2), а вектор
направлены вдоль оси вращения и связаны
с направлением вращения правилом правого
винта (рис. Т.2), а вектор![]() направлен так же, как вектор
направлен так же, как вектор![]() ,
если вращение ускоренное, и противоположно
вектору
,
если вращение ускоренное, и противоположно
вектору![]() ,
если движение замедленное. Итак, если
движение происходит вокруг неподвижной
оси, все перечисленные величины направлены
вдоль одной прямой.
,
если движение замедленное. Итак, если
движение происходит вокруг неподвижной
оси, все перечисленные величины направлены
вдоль одной прямой.
В разделе Динамика вращательного движениянаряду с понятиями силы и массы вводятся понятиямомента силы и момента инерции.
Момент силы. Покажем, что для характеристики вращательного движения понятия силы недостаточно. Пусть к коромыслу (рис.Т.3) слева от оси вращенияОна расстоянии 0,2 м приложена сила 2 Н, которая стремится повернуть его против часовой стрелки. Опыт говорит о том, что уравновесить коромысло можно несколькими способами.Например, можно справа от оси на расстоянии 0,4 м приложить силу1 Н (рис. Т.3а), а можно приложить силу 4 Н, но на расстоянии 0,1 м от оси вращения (рис. Т.3б).
Таким образом, вращающий эффект силы зависит от расстояния не в меньшей степени, чем от самой силы.
Рис. Т.3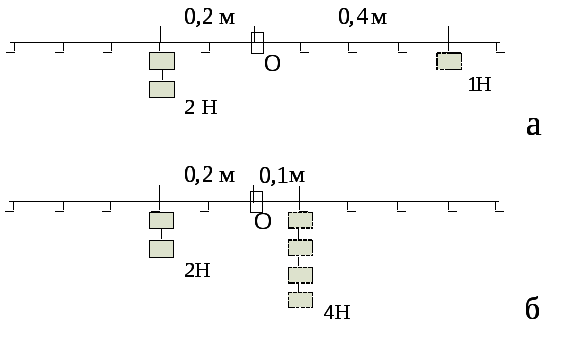
Величина, характеризующая вращающий эффект силы, называетсямоментом силы. Различают момент силы относительно точки и момент силы относительно оси.
М
Рис. Т.4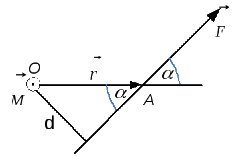
![]() (рис. Т.4). Моментом силы
(рис. Т.4). Моментом силы![]() относительно точкиОназы-вается
вектор
относительно точкиОназы-вается
вектор![]() ,
определяемый векторным произведением
радиуса-вектора точки приложения силы
,
определяемый векторным произведением
радиуса-вектора точки приложения силы
![]() (радиуса-вектора, проведенного из точкиОв точку приложения силы А), и силы:
(радиуса-вектора, проведенного из точкиОв точку приложения силы А), и силы:
![]() .
(Т.6)
.
(Т.6)
Из формулы (Т.6) следует,
что вектор
![]() направлен перпендикулярно
плоскости, в которой лежат векторы
направлен перпендикулярно
плоскости, в которой лежат векторы![]() и
и![]() ,
причем так, чтонаправление
вектора
,
причем так, чтонаправление
вектора
![]() совпадает снаправлением
поступательного движения правоговинта при его
вращении от первого вектора
совпадает снаправлением
поступательного движения правоговинта при его
вращении от первого вектора
![]() ко второму
ко второму![]() в сторону меньшего угла. На рис. Т.4векторы
в сторону меньшего угла. На рис. Т.4векторы
![]() и
и
![]() лежат в плоскости рисунка, авектор
лежат в плоскости рисунка, авектор
![]() направлен перпендикулярно плоскости
рисунка, т. е. на нас (изображен точкой
в кружочке).
направлен перпендикулярно плоскости
рисунка, т. е. на нас (изображен точкой
в кружочке).
Из формулы (Т.6) также следует, что модуль момента силы Мравен
![]() ,
(Т.7)
,
(Т.7)
где
![]() – плечо силы
– плечо силы![]() относительно точкиО(плечом силы
называется длина перпендикуляра,
опущенного из точкиОна прямую,
вдоль которой действует сила),
относительно точкиО(плечом силы
называется длина перпендикуляра,
опущенного из точкиОна прямую,
вдоль которой действует сила),![]()
![]() – угол между векторами
– угол между векторами![]() и
и![]() .
.
Момент силы относительно
осихарактеризует способность силы
вращать тело вокруг данной оси. Пусть
к телу, закрепленному на осиОО(рис. Т.5), в точкеАприложена сила![]() .
.
а б
Рис. Т.5
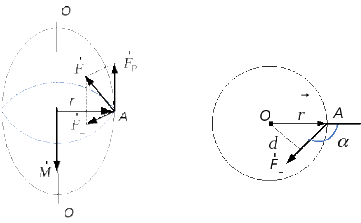
Эту силу можно разложить
на две составляющие (рис. Т.5а):
![]() – параллельную оси, и
– параллельную оси, и![]() – лежащую в плоскости, перпендикулярной
оси. Очевидно, что сила
– лежащую в плоскости, перпендикулярной
оси. Очевидно, что сила![]() не может вызвать вращения тела вокруг
осиОО. Вращение тела вокруг осиООможет вызвать только сила
не может вызвать вращения тела вокруг
осиОО. Вращение тела вокруг осиООможет вызвать только сила![]() .
.
Таким образом, момент какой угодно силы относительно неподвижной оси сводится к моменту составляющей этой силы, лежащей в плоскости, перпендикулярной оси.
На рис. Т.5б изображено
сечение тела, перпендикулярное оси ОО,
в котором и лежит сила![]() .
Сравнив рис. Т.5б с рис. Т.4, видим, что они
аналогичны. Это значит, что вектор
момента силы
.
Сравнив рис. Т.5б с рис. Т.4, видим, что они
аналогичны. Это значит, что вектор
момента силы![]() относительно точкиО(точки пересечения
оси с плоскостью, в которой лежит вектор
относительно точкиО(точки пересечения
оси с плоскостью, в которой лежит вектор![]() )
может быть определен по формуле (Т.6),
согласно которой он направлен вдоль
оси вращения (направления указаны на
рисунке), а его модуль определяется по
(Т.7), т. е. он равен произведению силы
)
может быть определен по формуле (Т.6),
согласно которой он направлен вдоль
оси вращения (направления указаны на
рисунке), а его модуль определяется по
(Т.7), т. е. он равен произведению силы![]() на
ее плечо
на
ее плечо![]() .
.
В дальнейшем мы будем иметь дело только с моментом силы относительно неподвижной оси и соответственно будем рассматривать только силы, перпендикулярные к оси. В этом случае модуль момента силы определяется как произведение силы на ее плечо (кратчайшее расстояние от точки О, через которую проходит ось вращения, до линии действия силы):
![]() .
.
За направление момента силы принято считать то, в котором будет двигаться направленный вдоль оси буравчик, если его рукоятка поворачивается по направлению силы.
Момент инерции. Известно, что тела обладают инертностью (или инерцией). Инертность – это свойство тела, заключающееся в том, что при отсутствии внешних сил (или когда внешние силы взаимно уравновешены) тело сохраняет неизменным состояние своего движения – покоится или движется равномерно и прямолинейно. Если же на тело действует результирующая сила, то инертность сказывается в том, что изменение его скорости происходит постепенно, а не мгновенно. При этом изменение скорости тела происходит тем медленнее, чем больше его инертность. При поступательном движении мерой инертности тела является его масса. Это значит, чем больше масса тела, тем труднее изменить его скорость. Так, груженый вагон труднее разогнать и труднее остановить (если он движется), чем пустой.
При вращательном движении инертность тела зависит не только от его массы, но и от ее распределения относительно оси вращения. Поясним это на следующем примере. Пусть имеется система (рис. Т.6), состоящая из жесткого невесомого стержня и подвижных тяжелых грузов массы m.
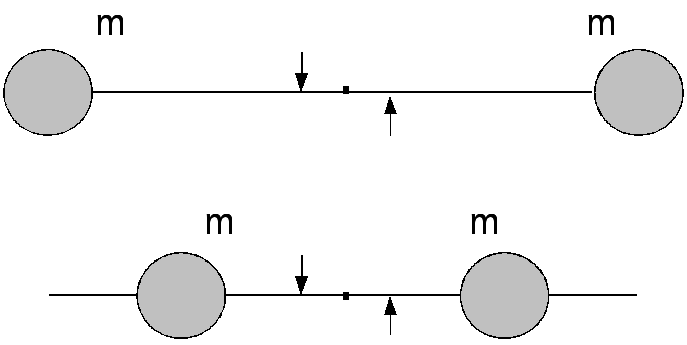
Рис. Т.6
Сначала закрепим грузы на концах стержня (рис. Т.6а) и, взявшись руками вблизи его центра масс, начнем раскручивать. Это достаточно трудно, если стержень длинный, а грузы тяжелые. Но если грузы переместить ближе к середине стержня (рис. Т.6б), то раскручивать его станет много легче (руки должны оставаться на прежнем месте, чтобы момент силы не изменился). Итак, при перемещении грузов инертность системы изменилась, хотя масса ее осталась прежней. Инертность тела (или системы тел), безусловно, зависит от его массы, но в гораздо большей степени от расположения массы относительно оси вращения.
Величина, характеризующая
инертность тела при вращательном
движении, называется моментом инерции
тела. Момент инерции материальной
точки относительно некоторой оси
вращения
![]() равен произведению
массы этой точки
равен произведению
массы этой точки
![]() на квадрат
ее расстояния до оси вращения
на квадрат
ее расстояния до оси вращения
![]()
![]() .
(Т.8)
.
(Т.8)
Момент инерции тела
(или системы материальных точек)
![]() относительно оси вращения равен
сумме моментов инерции его точек, т. е.
относительно оси вращения равен
сумме моментов инерции его точек, т. е.
![]() .
(Т.9)
.
(Т.9)
В случае непрерывного распределения массы суммирование сводится к интегрированию по объему тела V
![]() ,
(Т.10)
,
(Т.10)
где
![]() масса элементарного объема тела, все
точки которого одинаково удалены от
оси вращения.
масса элементарного объема тела, все
точки которого одинаково удалены от
оси вращения.
Формула (Т.10) позволяет сравнительно просто рассчитать момент инерции только для однородного тела правильной формы относительно оси симметрии, проходящей через его центр масс. Но если известен момент инерции тела относительно оси, проходящей через центр масс, то момент инерции относительно любой другой, параллельной ей оси, легко рассчитать по теореме Штейнера:
![]() ,
(Т.11)
,
(Т.11)
где I– момент инерции тела относительно
произвольной оси,
![]() – момент инерции относительно параллельной
ей оси, проходящей через центр масс
тела,
– момент инерции относительно параллельной
ей оси, проходящей через центр масс
тела,![]() – масса тела,
– масса тела,
![]() – расстояние от оси вращения до центра
масс тела.
– расстояние от оси вращения до центра
масс тела.
В случае сложной формы тела, когда теоретически трудно рассчитать момент инерции, прибегают к экспериментальным методам.
Итак, для описания вращательного движения вводятся величины, аналогичные тем, которыми характеризуют поступательное движение: момент силы аналогичен силе (при вращательном движении он играет ту же роль, что сила при поступательном), момент инерции аналогичен массе (при вращательном движении он играет ту же роль, что масса при поступательном).
Известно, что между аналогичными величинами существуют аналогичные соотношения. Поэтому, зная соотношения, установленные для поступательного движения, мы всегда можем записать соотношения, характеризующие вращательное движение.
Например, основной закон динамики (IIзакон Ньютона для поступательного движения) имеет вид
![]() ,
(Т.12)
,
(Т.12)
где
![]() – результирующая сила, действующая на
тело,
– результирующая сила, действующая на
тело,
![]() – масса тела,
– масса тела,
![]() – ускорение, полученное телом.
– ускорение, полученное телом.
Основной закон динамики вращательного движения (IIзакон Ньютона для вращательного движения) имеет аналогичный вид
![]() ,
(Т.13)
,
(Т.13)
где
![]() – результирующий момент сил, действующий
на тело,I– момент
инерции тела,
– результирующий момент сил, действующий
на тело,I– момент
инерции тела,![]() – угловое ускорение, полученное телом.
– угловое ускорение, полученное телом.
Используя формулу (Т.4), можно переписать (Т.13) в виде
![]() .
(Т.14)
.
(Т.14)
Введя обозначение
![]() ,
(Т.15)
,
(Т.15)
основному закону динамики вращательного движения (Т.13) можно придать другой вид
![]() ,
(Т.16)
,
(Т.16)
где
![]() – момент импульса,или кинетический
момент, твердого тела. Эта величина
аналогична импульсу точки
– момент импульса,или кинетический
момент, твердого тела. Эта величина
аналогична импульсу точки![]() .
.
Уравнение (Т.16),
называемое также уравнением моментов,
по виду аналогичноIIзакону Ньютона для поступательного
движения, представленному в виде![]() .
.
Из уравнения (Т. 16)
следует, что в тех случаях, когда
результирующий момент сил
![]() ,
действующий на тело (или систему тел),
равен нулю (система
тел замкнута),
,
действующий на тело (или систему тел),
равен нулю (система
тел замкнута),
 ,
и
,
и![]() .
(Т.17)
.
(Т.17)
Равенство (Т.17) представляет собой закон сохранения момента импульса и читается так: момент импульса замкнутой системы остается неизменным.
Представим аналогию величин и соотношений, характеризующих поступательное и вращательное движения, в виде таблицы
|
Поступательное движение |
Вращательное движение | ||
|
Перемещение |
|
Угол поворота |
|
|
Скорость |
|
Угловая скорость |
|
|
Ускорение |
|
Угловое ускорение |
|
|
Уравнение равномер-ного движения |
|
Уравнение равномер-ного вращения |
|
|
Уравнения равнопеременного движения |
|
Уравнения равнопеременного вращения |
|
|
Масса |
|
Момент инерции:
|
|
|
Сила |
|
Момент силы: 1) относительно точки, 2) относительно оси |
|
|
Основной закон динамики точки |
|
Основной закон динамики вращатель-ного движения |
|
|
Импульс точки Момент импульса точки |
|
Момент импульса твердого тела |
|
|
Работа силы |
|
Работа момента силы |
|
|
Кинетическая энергия точки |
|
Кинетическая энергия вращательного движения |
|