Вопрос 87. Классификация точек разрыва

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1. функция  определена в точке и ее окрестности;

2. существует конечный предел функции 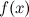 в точке ;

3. это предел равен значению функции в точке , т.е.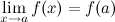 

называется точкой разрыва функции.

Точка разрыва первого рода

Определение

Если в точке  существуют конечные пределы  и , такие, что , то точка  называется точкой разрыва первого рода.

Точка разрыва второго рода

Определение

Если хотя б один из пределов  или  не существует или равен бесконечности, то точка называется точкой разрыва второго рода.

Точка устранимого разрыва

Определение

Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции  в точке :  или функция  не определена в точке , то точка  называется точкой устранимого разрыва

Вопрос 88. Определение непрерывности функции на отрезке.

Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Т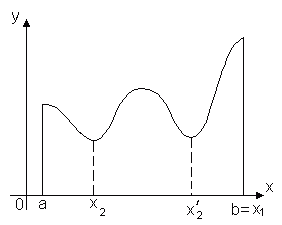еорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x₁ Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x₂ и x₂'.

Вопрос 89. Арифметические действия над непрерывными функциями

Вопрос 90. Теорема об устойчивости знака непрерывной функции

Вопрос 91. 1-ая теорема Больцано-Коши и ее геометрический смысл

Вопрос 92. Непрерывность сложной функции

Функция f(x) называется непрерывной в точке x₀, если .

Вопрос 93. Определение производной функции y f x

Вопрос 94. Геометрический смысл производной.

Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Вопрос 95. Физический смысл первой производной

Вопрос 96. Уравнение нормали к графику функции y f xв точке с абсциссой x=x₀

Вопрос 97. Уравнение касательной к графику функции y f x в точке с абсциссой x₌х₀ .

Вопрос 98. Определение дифференцируемой в точке функции.

Пусть функция  определена в некоторой окрестности точки . Если приращение функции  можно представить в виде , где A – постоянное число в точке ; - бесконечно малая функция при , то функция  называется дифференцируемой в точке .

Вопрос 99. Теорема о непрерывности функции, дифференцируемой в данной точке.

Если функция дифференцируема в некоторой точкеx=x_0, то она в этой точке непрерывна.

Вопрос 100. Производная суммы, произведения и частного двух функций.

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

Производная суммы двух функций.

Вопрос 101. Дифференцирование сложной функции.

Вопрос 102. Производные для функций: , . , x e xx, cos , sin x a xx, ctg , tg ln , , arcctg , xx x x x a log , arccos arctg x , tg , arcsin xx

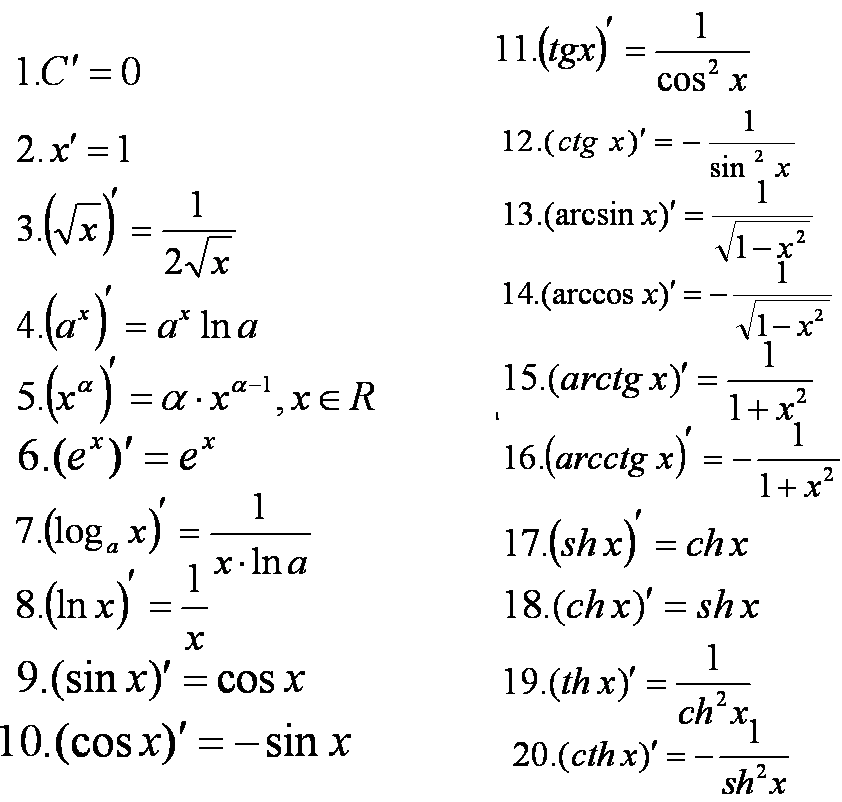
Вопрос 103. Теорема о дифференцировании сложной функции.

Вопрос 104. Производные функций, заданных неявно и параметрически

Производная параметрически заданной функции

Если функция fзаданапараметрически

x = φ(t), y = ψ(t), α < t < β,

где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

Производная неявно заданной функции

Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения

Вопрос 105. Понятие дифференциала и формула для вычисления дифференциала функции.

Вопрос 106. Геометрический смысл дифференциала

Проведем к графику функции  в точку  касательную  и рассмотрим ординату этой касательной для точки . На рисунке , . Из прямоугольного треугольника  имеем: , т.е. . Но, согласно геометрическому смыслу производной, . Поэтому  или . Это означает, что дифференциал функции  в  равен приращению ординаты касательной к графику функции в этой точке, когда  получает приращение .

Вопрос 107. Угол между двумя кривыми

Вопрос 108. Физический смысл второй производной