
- •Основные понятия информатики
- •Информационное моделирование и информационные модели
- •Алгоритмизация и программирование – инструментарий информатики
- •4. Дополнением множества Х называется разность I и Х (см. рис. 4).
- •Законы и тождества алгебры множеств:
- •5. Декартовым произведением двух непустых множеств Х и У называется множество ХхУ, состоящее из всех упорядоченных пар:
- •Типы отношений:
- •1) отношение эквивалентности.
- •2) отношение строгого порядка.
- •3) отношение нестрогого порядка.
- •Основные вопросы темы
- •1. Метод математической индукции.
- •2. Размещения, перестановки, сочетания.
- •1. Отрицание
- •2. Конъюнкция
- •3. Дизъюнкция
- •4. Импликация
- •5. Эквивалентность
- •Методы упрощения логических выражений. Методы решения логических задач

200 |
Информатика и математика |
|
|
A B == (A & B) (A & B).
Методы упрощения логических выражений. Методы решения логических задач
Рассмотрим пример решения логической задачи.
Пример 1. После обсуждения состава участников экспедиции решено, что должны выполняться два условия:
1.Если поедет Арбузов, то должны ехать Брюквин или Вишневский.
2.Если поедут Арбузов и Вишневский, то поедет Брюквин. Составить логическую формулу принятия решения в символической
форме, упростить полученную формулу и сформулировать по ней новое условие формирования экспедиции.
Введем переменные и соответствующие им элементарные высказыва-
ния.
A– поедет Арбузов;
Б– поедет Брюквин;
В – поедет Вишневский.
Тогда выработанные условия формирования экспедиции будут выглядеть следующим образом:
1. A →(Б В).
2. (A & Б)→ В.
Составим общую формулу и упростим выражение:
(A → (Б В))& ((A & Б)→ В)= (А Б В)& (А& В Б)= (А Б В)& (А В Б)= (А Б)& (В В)= (А Б)= А → Б.
т.е. если поедет Арбузов, то поедет Брюквин.
Пример 2. По подозрению в совершенном преступлении задержаны Браун, Джон и Смит. Один из них – уважаемый в городе старик, второй – чиновник, а третий – известный мошенник. В ходе следствия старик говорил правду, мошенник лгал, а третий задержанный в одном случае говорил правду, а в другом лгал.
Вот что они говорили:
Браун: Я совершил это. Джон не виноват (Б&¬Д); Джон: Браун не виноват. Преступник Смит (¬Б&С); Смит: Я не виноват. Виноват Браун (¬С&Б).
Опишем эти высказывания формально:
Б– преступление совершил Браун;
Д– преступление совершил Джон;
С – преступление совершил Смит.
Тогда их слова описываются следующими выражениями: Браун: Б & Д ;

2. План-конспект лекционного курса |
201 |
|
|
|
|
Джон: Б&C ; Смит: С& Б .
Так как по условиям задачи две из этих & ложны и одна истинна, то
L = (Б & Д) (Б & C) (С& Б).
Составим таблицу истинности:
№ |
|
Д |
С |
Б & |
|
|
|
|
&C |
|
|
& Б |
|
|
Б |
Д |
L |
||||||||||||
|
|
Б |
С |
|||||||||||
1 |
0 |
0 |
0 |
0 |
|
|
0 |
|
0 |
0 |
||||
2 |
0 |
0 |
1 |
0 |
|
|
1 |
|
0 |
1 |
||||
3 |
0 |
1 |
0 |
0 |
|
|
0 |
|
0 |
0 |
||||
4 |
0 |
1 |
1 |
0 |
|
|
1 |
|
0 |
1 |
||||
5 |
1 |
0 |
0 |
1 |
|
|
0 |
|
1 |
1 |
||||
6 |
1 |
0 |
1 |
1 |
|
|
0 |
|
0 |
1 |
||||
7 |
1 |
1 |
0 |
0 |
|
|
0 |
|
1 |
1 |
||||
8 |
1 |
1 |
1 |
0 |
|
|
0 |
|
0 |
0 |
||||
1.Исключим из рассмотрения те наборы, на которых L = 0 (по условию задачи одна из & – истинна, следовательно, L =1 ), 1, 3, 8.
2.Исключим случай 5, так как в нем две & истинны, что противоречит условию задачи.
3.В случаях 4, 6, 7 у нас в начальном наборе две 1 , т.е. 2 преступника, а по условию задачи он один.
Остается только случай 2 , т.е. преступник Смит и оба его высказывания ложны.
С& Б = 0 , следовательно, Б – ложно и С – истинно; Б& C =1= 1 – Джон – уважаемый старик.
Остается, что Браун – чиновник, и поскольку Б – ложно , то Д – истинно.
Пользуясь законами и тождествами Булевой алгебры, можно упрощать логические выражения.
Равносильные преобразования формул
Используя равносильности, можно часть формулы или всю формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными. (Аналог тождественным преобразованиям в арифметике, алгебре и тригонометрии.)
Равносильные преобразования используются для доказательства равносильностей, приведения формул к заданному виду, упрощения формул.
Формула А считается проще равносильной ей формулы В, если она содержит меньше букв, меньше логических операций. При этом обычно

202 |
Информатика и математика |
|
|
операции эквивалентность и импликация заменяются операциями дизъюнкция и конъюнкция, а отрицаниеотносят к элементарным высказываниям.
Для удобства использования и ссылок при проведении равносильных преобразований перечень наиболее часто употребляемых равносильностей (законов логических операций над высказываниями) можно свести в единую таблицу, в которой рассмотренные выше равносильности даны в сквозной нумерации.
При проведении равносильных преобразований каждый шаг основывается на использовании того или иного закона. Номер соответствующей формулы (из общей таблицы) мы будем указывать над знаком равносильности, предшествующим очередному шагу.
Рассмотрим ряд примеров равносильных преобразований. Пример 1. Доказать равносильность x ↔ y ≡ x y x y .
19 |
18 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
||||||||
x ↔ y ≡(x → y) ( y → x) ≡( |
x |
y) ( |
y |
x) ≡( |
x |
y) |
y |
( |
x |
y)x ≡ |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
3 |
|
|
|
|
|||||
≡ x y x x y y y x ≡ x y 0 |
0 y x ≡ x y y |
x ≡ x y x y. |
||||||||||||||||||||||||||||||||
Пример 2. Упростить формулу ( |
|
→ x y) y ≡ A . |
|
|
|
|
|
|||||||||||||||||||||||||||
x y |
|
|
|
|
|
|||||||||||||||||||||||||||||
18 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
П |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
A ≡(x y x y) y ≡(x y x y) y ≡(x y) y ≡ y . |
|
|
|
|
|
|||||||||||||||||||||||||||||
Предикаты
Валгебре логики высказывания рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности.
Ни структура высказываний, ни тем более их содержание не затрагиваются. В то же время и в науке, и в практике используются заключения, существенным образом зависящие как от структуры, так и от содержания используемых в них высказываний.
Например, в рассуждении: «Всякий ромб – параллелограмм; АВСD – ромб; следовательно, АВСD – параллелограмм» – посылки и заключение являются элементарными высказываниями логики высказываний и с точки зрения этой логики рассматриваются как целые, неделимые, без учета их внутренней структуры. Следовательно, алгебра логики, будучи важной частью логики, оказывается недостаточной в анализе многих рассуждений.
Всвязи с этим возникает необходимость в расширении логики высказываний, в построении такой логической системы, средствами которой можно было бы исследовать структуру тех высказываний, которые в рамках логики высказываний рассматриваются как элементарные.
Такой логической системой является логика предикатов, содержащая всю логику высказываний в качестве своей части.
Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально – подлежащее, хотя оно может играть и роль дополнения) и предикат (буквально – сказуемое, хотя оно может играть и роль определения).
2. План-конспект лекционного курса |
203 |
|
|
|
|
Субъект – это то, о чем что-то утверждается в высказывании; предикат – это то, что утверждается о субъекте.
Например, в высказывании «7 – простое число», «7» – субъект, «простое число» – предикат. Это высказывание утверждает, что «7» обладает свойством «быть простым числом».
Если в рассмотренном примере заменить конкретное число 7 переменной х из множества натуральных чисел, то получим высказывательную форму «х – простое число». При одних значениях х (например, х=13, х=17) эта форма дает истинные высказывания, а при других значениях х (например, х=10, х=18) эта форма дает ложные высказывания.
Ясно, что эта высказывательная форма определяет функцию одной переменной х, определенной на множестве N, и принимающую значения из множества {1;0}. Здесь предикат становится функцией субъекта и выражает свойство субъекта.
Дадим несколько определений, относящихся к предикатам. Одноместным предикатом Р(x) называется произвольная функция
переменного x, определенная на множестве M и принимающая значение из множества {1; 0}.
Множество М, на котором определен предикат Р(x), называется обла-
стью определения предиката Р(x).
Множество всех элементов x M , при которых предикат принимает значения «истина» (1), называется множеством (областью) истинности
предиката Р(x), т.е. множество истинности предиката Р(х) – это |
множест- |
|
воI p ={x : x M , P(x) =1}, или иначе: M [P], или так: |
M [P(x)]. Так, |
например, |
x |
x |
|
предикат Р(x) – «x – простое число» определен на множестве N, а множество истинности IP для него есть множество всех простых чисел.
Предикат Q(x) – «sinx=0» определен на множестве R, а его множеством истинности является IQ ={kπ, k Z}.
Предикат F(x) – «диагонали параллелограмма x взаимно перпендикулярны» определен на множестве всех параллелограммов, а его множеством истинности является множество всех ромбов.
Из приведенных примеров видим, что одноместные предикаты вы-
ражают свойства предметов (субъектов).
Предикат Р(х), определенный на множестве М, называется тождественно истинным, если его множество истинности совпадает с областью определения, т. е. Ip=M.
Предикат Р(х), определенный на множестве М, называется тождественно ложным, если его множество истинности является пустым множеством, т.е. Ip=0.
204 |
Информатика и математика |
|
|
Естественным обобщением понятия одноместного предиката является понятие многоместного предиката, с помощью которого выражаются отношения между предметами.
Примером бинарного отношения, т.е. отношения между двумя предметами, является отношение «меньше». Пусть это отношение введено на множестве Z целых чисел. Оно может быть охарактеризовано высказывательной формой «х<y», где x, y Z , т.е. является функцией двух перемен-
ных Р(х,y), определенной на множестве упорядоченных пар целых чисел ZхZ=Z2 c множеством значений {1;0}.
Двухместным предикатом Р(x,y) называется функция двух переменных x и y, определенная на множестве М=М1хМ2 и принимающая значения из множества {1;0}.
В числе примеров двухместных предикатов можно назвать такие предикаты:
•Q(x, y) – «x=y» – предикат равенства, определенный на множестве
RхR=R2;
•F(x,y) – «х параллелен y»;
•«прямая х параллельна прямой y», определенный на множестве прямых, лежащих на данной плоскости.
Совершенно аналогично вводится понятие трехместного предиката. Приведем пример трехместного предиката (функции трех переменных): S(x,y,z) – «x+y=z». Подстановка в него х=3 превращает его в двухместный предикат: S(y,z) – «3+y=z», а подстановка х=3, z=2 – в одноместный предикат S(y) – «3+y=2». Подстановка же S(2,3,5) превращает его в истинное высказывание, а S(1,7,4)– в ложное.
Аналогично определяется и n-местный предикат (функция n переменных). Пример п-местного предиката:
R(x1, x2,…,xn): a1 x1+…+anxn=0,
который, как видим, представляет собой алгебраическое уравнение с n неизвестными.
При n=0 будем иметь нульместный предикат – это логическая (пропозициональная) переменная, принимающая значения из множества {1;0}.
Логические операции над предикатами
Предикаты так же, как высказывания, могут принимать два значения: «истина» (1) и «ложь» (0), поэтому к ним применимы все операции логики высказываний, в результате чего из элементарных предикатов формируются сложные предикаты (как и в логике высказываний, где из элементарных высказываний формировались сложные, составные). Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов. Эти операции в логике предикатов сохраняют тот же смысл, который был им присвоен в логике высказываний.
ПустьнанекотороммножествеM определеныдвапредикатаP(x) иQ(x).

2. План-конспект лекционного курса |
205 |
|
|
|
|
Конъюнкцией двух предикатов P(x) и Q(x) называется новый (сложный) предикат P(x) Q(x) , который принимает значение «истина» при тех и только тех значениях x M , при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях.
Очевидно, что областью истинности предиката P(x) Q(x) является общаячастьобластиистинностипредикатовP(x) иQ(x), т.е. пересечение I P ∩ IQ .
Так, например, для предикатов P(x): «x – четное число» и Q(x): «x кратно 3» конъюнкцией P(x) Q(x) является предикат «x – четное число и x кратно 2», т.е. предикат «x делится на 6».
Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат P(x) Q(x) , который принимает значение «ложь» при тех и только тех значениях x M , при которых каждый из предикатов принимает значение «ложь», и принимает значение «истина» во всех остальных случаях.
Ясно, что областью истинности предиката P(x) Q(x) является объединение области истинности предикатов P(x) и Q(x), т.е. I P IQ .
Отрицанием предиката P(x) называется новый предикат P(x) илиP(x) , который принимает значение «истина» при всех значениях x M , при которых предикат P(x) принимает значение «ложь», и принимает значение «ложь» при тех значениях x M , при которых предикат P(x) принимает значение «истина».
Очевидно, что I P = I P , т.е. множество истинности предиката P(x) яв-
ляется дополнением к множеству IP.
Импликацией предикатов P(x) и Q(x) называется новый предикат P(x) →Q(x) , который является ложным при тех и только тех значениях x M , при которых одновременно P(x) принимает значение «истина», а Q(x) – значение «ложь», и принимает значение “истина» во всех остальных случаях.
Поскольку при каждом фиксированном x M справедлива равносиль-
18
ность P(x) → Q(x) ≡P(x) Q(x) , то I P→Q = I P IQ .
Эквиваленцией предикатов P(x) и Q(x) называется новый предикат P(x) ↔ Q(x) , который обращается в «истину» при всех тех и только тех x M , при которых P(x) и Q(x) обращаются оба в истинные или оба в ложные высказывания.
Для его множества истинности имеем: I P↔Q = I P ∩ IQ I P ∩ IQ .

206 Информатика и математика
Кванторы
Рассмотрим операции, преобразующие предикаты в высказывания. Пусть имеется предикат Р(х), определенный на множестве М. Если
«а» – некоторый элемент из множества М, то подстановка его вместо х в предикат Р(х) превращает этот предикат в высказывание Р(а). Такое высказывание называют единичным. Например, r(x): «х – четное число» – предикат, а r (6) – истинное высказывание, r (3) – ложное высказывание.
Это же относится и к n-местным предикатам: если вместо всех предметных переменных хi, i=1, n подставить их значения, то получим высказывание.
Наряду с образованием из предикатов высказываний в результате таких подстановок в логике предикатов рассматриваются еще две операции, которые превращают одноместный предикат в высказывание. Эти операции называются операциями квантификации (или просто квантификацией, или связыванием кванторами, или навешиванием кванторов). При этом рассматриваются, соответственно, два типа так называемых кванторов.
Квантор всеобщности. Пусть Р(х) – предикат, определенный на мно-
жестве М. Под выражением xP(x) понимают высказывание истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение звучит так: «Для всякого х Р(х) истинно».
Символ называют квантором всеобщности (общности). Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании же х называют связанной
квантором всеобщности.
Квантор существования. Пусть P(x) – предикат, определенный на множестве М. Под выражением xP(x) понимают высказывание, которое является истинным, если существует элемент x M , для которого P(x) истинно, и ложным – в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение звучит так: «Существует x, при котором P(x) истинно». Символ называют квантором существования. В высказывании переменная x связана этим квантором (на нее навешен квантор).
Кванторные операции применяются и к многоместным предикатам. Пусть, например, на множестве М задан двухместный предикат P(x,y). Применение кванторной операции к предикату P(x,y) по переменной x ставит в соответствие двухместному предикату P(x,y) одноместный предикатxP(x, y) (или одноместный предикат xP(x, y) ), зависящий от переменной
y и не зависящий от переменной x. К ним можно применить кванторные операции по переменной y, которые приведут уже к высказываниям сле-
дующих видов: y xP(x, y), y xP(x, y), y xP(x, y), y xP(x, y).

2. План-конспект лекционного курса |
207 |
|
|
|
|
Рассмотрим предикат P(x), определенный на множестве M={a1,…,an}, содержащем конечное число элементов. Если предикат P(x) является тож- дественно-истинным, то истинными будут высказывания P(a1),P(a2),…,P(an). При этом истинными будут высказывания xP(x) и
конъюнкция P(a1 ) P(a2 ) ... P(an ) .
Если же хотя бы для одного элемента ak M P(ak) окажется ложным,
n
то ложными будут высказывание xP(x) и конъюнкция P(ai ) . Следова-
i=1
n
тельно, справедлива равносильность xP(x) ≡ P(a1 ) P(a2 ) ... P(an ) = P(ai ) .
i=1
Численные кванторы. В математике часто встречаются выражения вида: «по меньшей мере n» («хотя бы n»), «не более чем n», «n и только n» («ровно n»), где n – натуральное число.
Эти выражения, называемые численными кванторами, имеют чисто логический смысл; они могут быть заменены равнозначными выражениями, не содержащими числительных и состоящими только из логических терминов и знака≡ или ~, означающего тождество (совпадение) объектов.
Пусть n=1. Предложение «По меньшей мере один объект обладает свойством P» имеет тот же смысл, что и предложение «Существует объект, обладающий свойством P», т.е. x(P(x)). (*)
Предложение «не более чем один объект обладает свойством P» равнозначно предложению «если есть объекты, обладающие свойством P, то они совпадают», т.е. x y(P(x) P( y) x ≡ y) (**). Предложение «один и только один объект обладает свойством P» равнозначно конъюнкции вышеуказанных предложений (*) и (**).
Отрицание предложений с кванторами. Условимся отрицание пред-
ложения |
x(P(x)) записывать как |
|
x(P(x)) , а отрицание |
предложения |
||||
x(P(x)) |
– как |
|
x(P(x)) . Очевидно, что предложение |
|
x(P(x)) |
имеет тот же |
||
|
|
|||||||
смысл, а следовательно, то же значение истинности, что и предложениеx(P(x)) , а предложение x(P(x)) – тот же смысл, что x(P(x)) . Иначе говоря,x(P(x)) равносильно x(P(x)) ; x(P(x)) равносильно x(P(x)) .
Кванторы общности и существования называют двойственными относительно один другого. Выясним теперь, как строить отрицание предложе-
ния, |
|
|
начинающегося с нескольких кванторов, |
например, такого: |
||||||
x y z(P(x, y, z)) . |
|
|||||||||
чим: |
Последовательно применяя сформулированное выше правило, полу- |
|||||||||
|
|
|
|
x y z(P(x, y, z)) равносильно x( |
|
y z(P(x, y, z)) , |
что равносильно |
|||
|
|
|
|
|
||||||
x y( |
|
z(P(x, y, z))) , что равносильно x y z( |
|
(x, y, z)) . |
|
|||||
|
P |
|
||||||||

208 |
Информатика и математика |
|
|
2. В логике предикатов будем пользоваться следующей символикой:
1.Символы p, q, r, … – переменные высказывания, принимающие два значения: 1 – истина , 0 – ложь.
2.Предметные переменные – x, y, z, … , которые пробегают значения
из некоторого множества М;
x0, y0, z0 – предметные константы, т.е. значения предметных переменных.
3.P(·), Q(·), F(·), … – одноместные предикатные переменные;
Q(·,·,…,·), R(·,·, …,·) – n-местные предикатные переменные. P0(·), Q0(·,·, …,·) – символы постоянных предикатов.
4.Символы логических операций: , , →,−.
5.Символы кванторных операций: x, x.
6.Вспомогательные символы: скобки, запятые.
Определение формулы логики предикатов.
1.Каждое высказывание, как переменное, так и постоянное, является формулой (элементарной).
2.Если F(·,·, …,·) – n-местная предикатная переменная или постоян-
ный предикат, а x1, x2,…, xn– предметные переменные или предметные постоянные (не обязательно все различные), то F(x1, x2,…, xn) есть формула. Такая формула называется элементарной, в ней предметные переменные являются свободными, не связанными кванторами.
3.Если А и В – формулы, причем такие, что одна и та же предметная переменная не является в одной из них связанной, а в другой – свободной, то слова A B, A B, A → B есть формулы. В этих формулах те переменные,
которые в исходных формулах были свободны, являются свободными, а те, которые были связанными, являются связанными.
4.Если А – формула, то A – формула, и характер предметных переменных при переходе от формулы А к формуле A не меняется.
5.Если А(х) – формула, в которую предметная переменная х входит свободно, то слова xA(x) и xA(x) являются формулами, причем предмет-
ная переменная входит в них связанно.
6. Всякое слово, отличное от тех, которые названы формулами в пунктах 1 – 5, не является формулой.
Например, если Р(х) и Q(x,y) – одноместный и двухместный предикаты, а q, r – переменные высказывания, то формулами будут, например, слова (выражения):
q, P(x), P(x) Q(x0 , y), xP(x) → xQ(x, y), (Q(x, y) q) → r .
Не является формулой, например, слово: xQ(x, y) → P(x) . Здесь нарушено условие п. 3, так как в формулу xQ(x, y) переменная х входит связанно, а в формулу Р(х) переменная х входит свободно.

2. План-конспект лекционного курса |
209 |
|
|
|
|
Из определения формулы логики предикатов ясно, что всякая формула алгебры высказываний является формулой логики предикатов.
Логическое значение формулы логики предикатов зависит от значений трех видов переменных: 1) значений входящих в формулу переменных высказываний; 2) значений свободных предметных переменных из множества М; 3) значений предикатных переменных.
При конкретных значениях каждого из трех видов переменных формула логики предикатов становится высказыванием, имеющим истинное или ложное значение.
В качестве примера рассмотрим формулу y z(P(x, y) → P( y, z)) , в которой двухместный предикат Р(x, y) определен на множестве M×M, где
M={0,1,2,…,n,…}, т.е. M×M=N×N.
В формулу входят переменный предикат P(x,y), предметные переменные x,y,z, две из которых y и z – связанные кванторами, а x – свободная.
Возьмем за конкретное значение предиката P(x,y) фиксированный предикат P0(x,y): «x<y», а свободной переменной х придадим значение x0 = 5 M . Тогда при значениях y, меньших x0=5, предикат P0(x0,y) принимает значение «ложь», а импликация P(x, y) → P( y, z) при всех z M при-
нимает значение «истина», т.е. высказывание y z(P0 (x, y) → P0 ( y, z)) имеет значение «истина».
Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.
Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.
Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей.
Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, не содержащая х). Тогда имеют место равносильности:
1. xA(x) ≡ x A(x). 2. xA(x) ≡ x A(x). 3. xA(x) ≡ x A(x).
4. xA(x) ≡ x A(x).
5. xA(x) xB(x) ≡ x[A(x) B(x)] . 6. C xB(x) ≡ x[C B(x)] .
7. C xB(x) ≡ x[C B(x)] . 8. C → xB(x) ≡ x[C → B(x)].
210 |
Информатика и математика |
|
|
9.x[B(x) →C] ≡ xB(x) →C.
10.x[A(x) B(x)] ≡ xA(x) xB(x).
11.x[C B(x)] ≡ C xB(x).
12.x[C B(x)] ≡ C xB(x).
13.xA(x) yB( y) ≡ x y[A(x) B( y)].
14.x[C → B(x)] ≡ C → xB(x).
15.x[B(x) → C] ≡ xB(x) → C.
Равносильность 1 означает тот простой факт, что если не для всех х истинно А(х), то существует х, при котором будет истиной A(x) .
Равносильность 2 означает тот факт, что если не существует х, при котором истинно А(х), то для всех х будет истиной A(x) .
Равносильности 3 и 4 получаются из равносильностей 1 и 2, соответственно, если от обеих их частей взять отрицания и воспользоваться законом двойного отрицания.
Подробнее см.: 1, 4.
ЗАКЛЮЧЕНИЕ
Информатика является молодой быстроразвивающейся отраслью науки и индустрии. Продукты и услуги информатики широко используются в юриспруденции.
Все это показывает, насколько важно современному юристу знать основы информатики и уметь использовать ее достижения в своей профессиональной деятельности.
ЛИТЕРАТУРА
Основная
1.Дубинина Н.М., Казанцева С.Я. Информатика и математика для юристов: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2011.
2.Егоров А.В, Котов Э.М. Информационные системы в юриспруденции: Учебник для вузов. – М.: Феникс, 2008.
3.Информатика: практикум по работе на компьютере / Под ред. Н.В. Макарова. – М.: Финансы и статистика, 2008.
4.Колмогоров А.Н., Драгалин А.Г. Введение в математическую логику. – М.: Изд-во МГУ, 2007.
5.Мельников В.П. Информационная безопасность и защита информации. – М.: ACADEMIA, 2007.
6.Попов А.М., Сотников В.Н., Нагаева Е.И. Информатика и математика для юристов. – М.: ЮНИТИ-ДАНА, 2009.

3. КОНСУЛЬТАЦИОННЫЙ КУРС
Авторы-составители: канд. физ.-мат. наук, проф. О.Ю. Худякова, канд. техн. наук, доц. В.А. Бужинский
ВВЕДЕНИЕ
Для консультационного курса по дисциплине «Информатика и математика» отобран комплекс вопросов, вызывающих у студентов особый практический интерес при изучении курса, а также наиболее сложные для самостоятельного изучения.
1 ЧЕМ ИНТРАНЕТ ОТЛИЧАЕТСЯ ОТ ИНТЕРНЕТА?
Компьютерные вычислительные сети принято делить на глобальные и локальные. Самый яркий пример глобальной сети – Интернет.
Локальная вычислительная сеть – это связанные между собой в единую информационную систему персональные компьютеры, принтеры, факсы, серверы и другое телекоммуникационное оборудование. Сеть дает возможность отдельным сотрудникам организации взаимодействовать между собой и обращаться к совместно используемым ресурсам; позволяет им получать доступ к данным, хранящимся на персональных компьютерах как в удаленных офисах, так и соседних ПК. Кроме того, правильная организация ЛВС обеспечивает информационную безопасность (исключает несанкционированный доступ к информационным блокам).
С помощью современного оборудования можно передавать большие информационные потоки данных не только по проводным линиям, но и по радиоканалу, что увеличивает эффективность и гибкость создаваемых локальных и корпоративных сетей связи.
Локальная сеть организации (предприятия), основанная на применении семейства протоколов TCP/IP и использовании для передачи и отображения информации протокола HTTP, называется Интранет (англ. Intranet; нередко также употребляется термин «интрасеть») – в отличие от Интернета, это внутренняя частная сеть организации. Как правило, Интранет – это Интернет в миниатюре, который построен на использовании протоколов ТСР/IP для обмена и совместного использования некоторой части информации внутри этой организации. Основанный на базовых протоколах HTTP и HTTPS и организованный по принципу клиент-сервер, интра- нет-сайт доступен с любого компьютера локальной сети через браузер.

212 |
Информатика и математика |
2 МОЖНО ЛИ НАЗВАТЬ ОПЕРАЦИОННЫЕ СИСТЕМЫ ИНСТРУМЕНТАЛЬНЫМ ПРОГРАММНЫМ ОБЕСПЕЧЕНИЕМ?
Все программное обеспечение делится на три больших класса: сис-
темное, инструментальное и прикладное.
Системное программное обеспечение – это совокупность программ и программных комплексов для обеспечения работы компьютера и сетей ЭВМ. К нему относятся операционные системы и оболочки, программы диагностики работоспособности компьютера, обслуживания сети, дисков, архивирования данных, антивирусные и другие.
Инструментальное программное обеспечение – это совокупность программ и программных комплексов для разработки, отладки и внедрения создаваемых программных продуктов. В эту группу входят трансляторы с различных алгоритмических языков, осуществляющие перевод текста программы на машинный язык; отладчики, с помощью которых обнаруживаются и устраняются ошибки, допущенные при написании программ; связывающие редакторы, позволяющие объединить отдельные части программ в единое целое; интегрированные среды разработчиков, объединяющие перечисленные компоненты в единую удобную для разработки программ систему.
Прикладное программное обеспечение – комплекс взаимосвязанных программ для решения задач в конкретной предметной области. К разновидностям прикладных программ относятся: текстовые, графические редакторы, электронные таблицы, базы данных, системы документооборота, бухгалтерские и финансовые программы и другие.
Следовательно, к системному программному обеспечению из предложенных вариантов программных продуктов относятся операционные системы.
3ДЛЯ ЧЕГО НУЖНЫ ЯЗЫКИ HTML И JAVA?
Впоследнее время высока популярность WWW-программирования. Языки WWW-программирования обладают рядом свойств, которые позволяют использовать их на платформе, специализированной для работы в качестве сервера. Чаще всего это интерпретаторы (такие как Perl, PHP) позволяющие использовать их на стороне сервера, или языки поддерживаемые клиентом (браузеры) – HTML, XML, Java, JavaScript, или специальные модули (plug-in), расширяющие клиента – Flash.
Проблемно-ориентированные языки позволяют быстро и эффективно писать программы для решения задач определенного класса. Управляющие конструкции и структуры данных в проблемно-ориентированных языках адекватно отражают характеристики той предметной области, для решения задач которой эти языки применяются. Примерами широко известных
3. Консультационный курс |
213 |
проблемно-ориентированных языков и классов решаемых ими задач могут служить:
•HTML – логическая разметка и структурирование текстов;
•TEX и LATEX – подготовка печатных документов;
•SQL – язык управления данными в реляционных СУБД;
•JPSS – язык имитационного моделирования.
Java – объектно-ориентированный язык программирования, разработанный компанией Sun Microsystems. Программы на Java транслируются в некоторую промежуточную форму (байт-код) небольшого размера, выполняемую виртуальной машиной Java (JVM). Программы на Java, в силу своего малого размера и возможности исполнения на любом устройстве, для которого существует соответствующая виртуальная машина, широко используются разработчиками игр для сотовых телефонов.
Pascal – язык программирования, первоначально предназначенный для обучения, в дальнейшем использовался для разработки прикладных программ.
Delphi – система разработки программного обеспечения, в состав которой входит компилятор языка Object Pascal.
C++ – объектно-ориентированный язык программирования, использующийся для разработки прикладных программных систем.
4 |
ПОЧЕМУ В НАЗВАНИЯХ ПРИКЛАДНЫХ ИНФОРМАЦИОННЫХ |
|
ПРОДУКТОВ ЧАСТО ВСТРЕЧАЕТСЯ СИМВОЛ ©? |
Знак охраны авторского права используется с именем физического или юридического лица, которому принадлежат авторские права. Также может быть указан объект защиты авторского права. Указывается год публикации или диапазон дат.
Знак охраны авторского права не создает дополнительных прав. Он только уведомляет, что авторские права принадлежат указанному физическому или юридическому лицу.
Отсутствие знака не означает что произведение не защищено авторскими правами, так как авторское право возникает в момент создания произведения и для защиты авторских прав не требуется регистрация произведения или соблюдение каких-либо иных формальностей.
Наличие или отсутствие знака охраны авторского права не влияет на лицензирование произведения в России. Но в странах, присоединившихся только к Всемирной конвенции об авторском праве, наличие знака является определяющим для предоставления защиты авторских прав в соответствии с п. 1 ст. III указанной конвенции в редакции 24 июля 1971 г.
Для признания и осуществления авторского права на программы для ЭВМ не требуется ее регистрация в какой-либо организации. Авторское

214 |
Информатика и математика |
право на программы для ЭВМ возникает автоматически при их создании. Для оповещения о своих правах разработчик программы может, начиная с первого выпуска в свет программы, использовать знак охраны авторского права, состоящий из трех элементов:
•символа ©;
•наименования (имени) правообладателя;
•года первого выпуска программы в свет.
Например, знак охраны авторских прав на текстовый редактор Microsoft Office Word 2007 выглядит следующим образом:
© Корпорация Microsoft, 1993–2007.
5 КАКИЕ СПРАВОЧНО-ПРАВОВЫЕ СИСТЕМЫ ИСПОЛЬЗУЮТСЯ СЕГОДНЯ?
Справочно-правовые системы (информационно-правовые системы) – особый класс компьютерных баз данных, содержащих тексты указов, постановлений и решений различных государственных органов. Кроме нормативных документов, они также содержат консультации специалистов по праву, бухгалтерскому и налоговому учету, судебные решения, типовые формы деловых документов и др.
На сегодняшний день в России и СНГ существует множество спра- вочно-правовых систем. К государственным системам относятся:
•Информационно-поисковая система «Закон» – база законодательства Государственной Думы РФ;
•Научно-технический центр правовой информации «Система» – эталонный банк правовых актов высших органов государственной власти;
•Информационно-правовая система «Законодательство России» – ГСРПА России;
•БД НЦПИ Минюста России;
•БД Министерства иностранных дел России.
К наиболее часто используемым на сегодня коммерческим системам относятся:
•Законпрост;
•Право.ру;
•ГАРАНТ;
•Консультант Плюс;
•Lexpro;
•Кодекс;
•Главбух;
•Референт.
|
3. Консультационный курс |
215 |
|
|
|
ЧТО ТАКОЕ КОМПЛЕКСНЫЕ ЧИСЛА И КАКИЕ ОПЕРАЦИИ |
|
|
6 |
|
|
|
|
НАД НИМИ ПРОИЗВОДЯТ? |
|
Множество R действительных чисел ограничено тем, что квадратные корни можно извлекать только из положительных чисел. Это создает большие неудобства при решении, например, алгебраических уравнений. Поэтому поле действительных чисел было расширено добавлением нового элемента i =  – 1 , который называется мнимой единицей. Мнимая единица не является действительным числом, но на нее распространили все алгебраические свойства действительных чисел. В результате появились новые элементы, которые записывают в виде и называют комплексными числами. Если b = 0 , то комплексное число является действительным. Поэтому действительные числа составляют часть комплексных чисел. По определению i2 = −1. Комплексные числа можно складывать и умножать:
– 1 , который называется мнимой единицей. Мнимая единица не является действительным числом, но на нее распространили все алгебраические свойства действительных чисел. В результате появились новые элементы, которые записывают в виде и называют комплексными числами. Если b = 0 , то комплексное число является действительным. Поэтому действительные числа составляют часть комплексных чисел. По определению i2 = −1. Комплексные числа можно складывать и умножать:
(a + bi) + (c + di) = (a + c) + (b + d)i ; (a + bi)(c + di) = (ac −bd) + (ad + bc)i .
Для каждого комплексного числа можно найти обратное:
1 |
|
= |
2 −3i |
= |
|
2 −3i |
= |
|
2 |
− |
|
3 |
i |
|
2 + |
3i |
(2 + 3i)(2 −3i) |
4 |
+ 9 + 0i |
13 |
13 |
||||||||
|
|
|
|
|
||||||||||
Операции сложения и умножения комплексных чисел подчиняются аксиомам, поэтому комплексное число образует поле. Открытие комплексных чисел позволило решить проблему алгебраических уравнений. Главный результат сформулирован в основной теореме алгебры:
Всякое алгебраическое уравнение степени n с комплексными коэффициентами имеет ровно n комплексных корней (теорема К.Гаусса).
Иоганн Бернулли и Леонард Эйлер открыли формулу eiα = cosα + i sin α ,
из которой при α = π следует eiπ = −1, что связывает мнимую единицу i с числами e,π и 1.
|
Каждое комплексное число геометрически представляет собой на |
|
плоскости точки с координатами (a, b) → a + bi . |
||
|
|
КАК ПОНИМАТЬ СЛОВОСОЧЕТАНИЕ КОРРЕЛЯЦИОННАЯ |
7 |
|
|
|
|
ЗАВИСИМОСТЬ? |
Рассмотрим пример. Между ростом и весом человека существует определенная зависимость. Однако много людей с одинаковым ростом имеют разный вес. Такая зависимость не является функциональной, поскольку для функций каждому х соответствует единственное значение у.
Можно предположить, что вес зависит не только от роста, но и от размера талии и прочих параметров, но она является очень сложной и пока никем не обнаружена. Можно считать, что вес человека зависит от ряда случайных величин, среди которых рост является одной из основных. Эту

216 |
Информатика и математика |
зависимость описывают с помощью понятия вероятности. Зависимости такого рода называются стохастическими, вероятностными или статистическими. Важнейшим видом здесь является корреляционная зависимость.
Рассмотрим в качестве примера вес и рост двадцати курсантов школы МВД (см. табл. 1.).
Таблица 1
Рост и вес курсантов школы МВД
Номер |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
курсанта |
||||||||||
Рост (см) |
178 |
170 |
181 |
173 |
169 |
178 |
177 |
165 |
187 |
182 |
Вес (кг) |
72 |
65 |
92 |
75 |
68 |
79 |
78 |
67 |
80 |
81 |
|
|
|
|
|
|
|
|
|
|
|
Номер |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
курсанта |
||||||||||
Рост (см) |
159 |
182 |
178 |
173 |
176 |
173 |
198 |
187 |
191 |
170 |
Вес (кг) |
56 |
82 |
77 |
63 |
80 |
65 |
85 |
89 |
87 |
72 |
Изобразим точки графически, откладывая по оси абсцисс – рост курсантов, по оси ординат – их вес (рис.1.).
Рис.1. Корреляционная зависимость между ростом и весом курсанта.
Точки лежат внутри некоторой области, или «облака». Заметно, что облако вытянуто вдоль какой – то наклонной прямой. Это означает, что Х и Y хорошо коррелированы, т.е. при увеличении роста вес, как правило, тоже увеличивается. Соединим точки отрезками, получим эмпирическую ломаную регрессии. При большем числе измерений эта ломаная больше похожа на прямую.
Прямая, к которой стремится ломаная, называется регрессией. Она является наилучшим решением задачи построения прямой, относительно которой сумма квадратов вертикальных отклонений экспериментальных точек будет наименьшей. Это задача метода наименьших квадратов.

3. Консультационный курс |
217 |
Уравнение искомой прямой имеет вид:
,
где
Здесь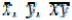 – средние значения роста, веса и их попарных произведений,
– средние значения роста, веса и их попарных произведений, 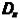 – дисперсия роста.
– дисперсия роста.
Подставим в формулы, получим:
Получим уравнение прямой: 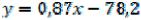 .
.
Это эмпирическое уравнение регрессии. Величина r, определяемая по формуле:
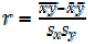 ,
,
называется коэффициентом корреляции.
Здесь 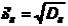 ,
, 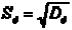 ,
, 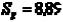 ,
, 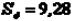 . Отсюда
. Отсюда
 .
.
Свойства коэффициента корреляции: 1. 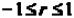 .
.
2. Если величины Х и Y независимы, то коэффициент корреляции равен нулю.
3. Если Х и Y связаны линейной зависимостью, то r = 1 или r = – 1, и наоборот.
При совместном изучении двух случайных величин Х и Y прежде всего находят величину коэффициента корреляции, и если он оказывается близким к единице, то имеет смысл описывать корреляционную связь.

218 |
Информатика и математика |
8 ВЧЕМ ОТЛИЧИЕ НЕПАРАМЕТРИЧЕСКИХ МЕТОДОВ ИССЛЕДОВАНИЯ ОТ ПАРАМЕТРИЧЕСКИХ?
Непараметрические методы в математической статистике – методы непосредственной оценки теоретического распределения вероятностей и тех или иных его общих свойств (симметрии и т.п.) по результатам наблюдений. Название непараметрические методы подчеркивает их отличие от классических (параметрических) методов, в которых предполагается, что неизвестное теоретическое распределение принадлежит какому-либо семейству, зависящему от конечного числа параметров (например, семейству нормальных распределений), и которые позволяют по результатам наблюдений оценивать неизвестные значения этих параметров и проверять те или иные гипотезы относительно их значений. Разработка непараметрических методов является в значительной степени заслугой советских ученых.
В качестве примера непараметрического метода можно привести найденный А. Н. Колмогоровым способ проверки согласованности теоретических и эмпирических распределений (так называемый критерий Колмогорова). Пусть результаты n независимых наблюдений некоторой величины имеют функцию распределения F (x) и пусть Fn (x) обозначает эмпирическую функцию распределения, построенную по этим n наблюдениям, a Dn
– наибольшее по абсолютной величине значение разности Fn (x) – F (x).
Случайная величина 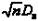 имеет в случае непрерывности F (x) функцию распределения Kn (x), не зависящую от F (x) и стремящуюся при безграничном возрастании n к пределу
имеет в случае непрерывности F (x) функцию распределения Kn (x), не зависящую от F (x) и стремящуюся при безграничном возрастании n к пределу
Отсюда при достаточно больших n для вероятности pn,x. Неравенства
получается приближенное выражение
pn,x = 1 – К (λ). (1)
Функция К (λ) табулирована. Ее значения для некоторых λ приведены в табл. 2.
|
|
Значения функции К (λ) |
|
Таблица 2 |
|||
|
|
|
|
|
|||
λ |
0,57 |
0,71 |
0,83 |
1,02 |
1,36 |
1,63 |
|
К (λ) |
0,10 |
0,30 |
0,50 |
0,75 |
0,95 |
0,99 |
|
Равенство (1) следующим образом используется для проверки гипотезы о том, что наблюдаемая случайная величина имеет функцию распределения F (x): сначала по результатам наблюдений находят значение величины Dn, а затем по формуле (1) вычисляют вероятность получения отклонения Fn от F, большего или равного наблюдаемому. Если указанная вероят-
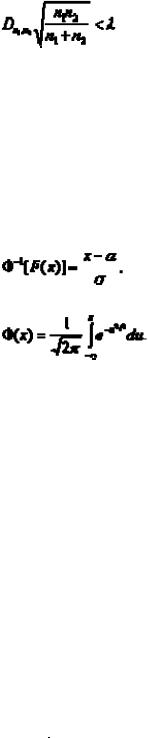
3. Консультационный курс |
219 |
ность достаточно мала, то в соответствии с общими принципами проверки статистических гипотез проверяемую гипотезу отвергают. В противном случае считают, что результаты опыта не противоречат проверяемой гипотезе. Аналогично проверяется гипотеза о том, получены ли две независимые выборки, объема n1 и n2 соответственно, из одной и той же генеральной совокупности с непрерывным законом распределения. При этом вместо формулы (1) пользуются тем, что вероятность неравенства
как это было установлено Н. В. Смирновым, имеет пределом К (λ), здесь Dn1, n2 есть наибольшее по абсолютной величине значение разности
Fn1 (х) – Fn2 (х).
Другим примером непараметрических методов могут служить методы проверки гипотезы о том, что теоретическое распределение принадлежит к семейству нормальных распределений. Отметим здесь лишь один из этих методов – так называемый метод выпрямленной диаграммы. Этот метод основывается на следующем замечании. Если случайная величина Х имеет нормальное распределение с параметрами а и σ, то
где Ф-1 – функция, обратная нормальной:
Т.о., график функции у = Ф-1[F (x)] будет в этом случае прямой линией, а график функции у = Ф-1[Fn (x)] – ломаной линией, близкой к этой прямой. Степень близости и служит критерием для проверки гипотезы нормальности распределения F (x).
9 |
ВЧЕМ ОСОБЕННОСТИ МАЛОЙ ВЫБОРКИ? |
Малые выборки, статистические выборки столь малого объема n, что к ним нельзя применить простые классические формулы, действующие лишь асимптотически при n  . Особенности статистической оценки парамет-
. Особенности статистической оценки парамет-
ров по малой выборке легче всего понять на примере нормального распределения (для которого малыми обычно считают выборки объема n ≤ 30). Пусть необходимо оценить неизвестное среднее значение a выборки x1, x2,
..., xn из нормальной совокупности с неизвестной дисперсией s2. Обозначим
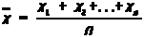 ,
,
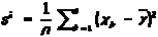 .
.
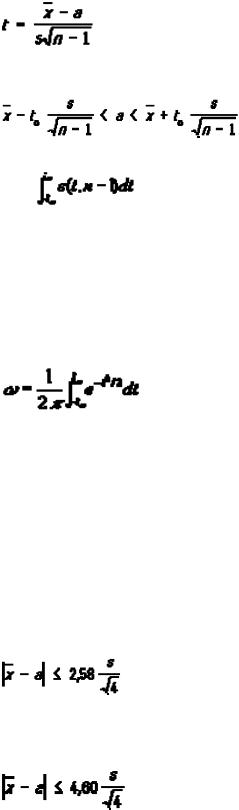
220 |
Информатика и математика |
Исходным пунктом при оценке a служит то обстоятельство, что распределение вероятностей величины
не зависит от параметров а и s.
Вероятность w неравенства – tw < t < tw и равносильного ему неравенства
вычисляется при этом по формуле |
(1) |
|
|
w = |
(2) |
где s (t, n – 1) есть плотность вероятности для так называемого распределения Стьюдента с n – 1 степенями свободы. Определяя для заданных n и w (0 < w < 1) критическое значение параметра Стьюдента tw (по соответствующим таблицам), получают правило нахождения доверительных границ для величины а, имеющей значимости уровень w.
При больших n формула (2), связывающая w и tw, приближенно может быть заменена формулой
(3)
Эту формулу иногда неправильно применяют для определения tw при небольших n, что приводит к грубым ошибкам. Так, для w = 0,99 по формуле (3) находим t0,99 = 2,58; истинные значения t0,99 для малых n приведены в следующей таблице 3.
Таблица 3
Значения параметра Стьюдента при малом объеме выборки
n |
2 |
3 |
4 |
5 |
10 |
20 |
30 |
t0,99 |
63,66 |
9,92 |
5,84 |
4,60 |
3,25 |
2,86 |
2,76 |
Если пользоваться формулой (3) при n = 5, то получится вывод, что неравенство
выполняется с вероятностью 0,99. В действительности в случае пяти наблюдений вероятность этого неравенства равна лишь 0,94, а вероятностью 0,99 обладает в соответствии с приведенной таблицей неравенство
Разработаны также аналогичные методы оценки по малым выборкам параметровмногомерныхраспределений(например, коэффициентакорреляции).

3. Консультационный курс |
221 |
10 КАК ОЦЕНИТЬ ДОСТОВЕРНОСТЬ РЕЗУЛЬТАТОВ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЙ?
Для определения пределов колеблемости, полученной по данным малой выборки средней величины и оценки достоверности различий сравниваемых средних (относительных величин) используют таблицу критерия t (Стьюдента).
В графах таблицы помещены величины доверительного коэффициента (t), показывающие, во сколько раз разность сравниваемых величин при данном малом числе наблюдений должна превышать свою среднюю ошибку для того, чтобы эта разность могла быть признана достоверной с данным уровнем вероятности, а результаты статистического исследования – достаточно надежными.
Значение коэффициента t Стьюдента зависит не только от вероятности (рt), но и от объема выборки (при n` = n-1). Ясно, что чем меньше выборка, тем больше значение t.
Обращаться к таблице следует по графе 1, в которой указано число степеней свободы n` = n-1, т.е. числу проведенных наблюдений, уменьшенному на единицу. Так, например, если после восьми испытаний действия спинномозговой анестезии на уровень кровяного давления установлено, что средняя величина снижения кровяного давления составляла 5,75 мм при средней ошибке 0,65, то из таблицы t видно, что при n` = 8-1 = 7; t =2,36. Это значит, что с вероятностью ошибки не более чем 5% можно утверждать, что размеры снижения кровяного давления при спинномозговой анестезии находятся в пределах 5,75±(2,36 х 0,65), т.е. в пределах 5,75±1,53 или от 4,22 до 8,26 мм; с вероятностью ошибки не более чем 1% можно утверждать, что размеры снижения кровяного давления в результате спинномозговой анестезии составляют 5,75±(3,50 х 0,65) или от 3.48 до 8,02 мм.
Если оценивается достоверность разности коэффициентов или сред-
них, т.е. 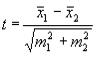 , то n1 + n2 – 2 .
, то n1 + n2 – 2 .
Среднее падение артериального давления при спинномозговой ане-
стезии 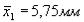 , а при эфирном наркозе
, а при эфирном наркозе 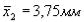 ; случайна ли разность средних или действительно эфирный наркоз вызывает меньшее падение артериального давления, чем спинномозговая анестезия?
; случайна ли разность средних или действительно эфирный наркоз вызывает меньшее падение артериального давления, чем спинномозговая анестезия?
Таблица 4
Падение артериального давления в зависимости от вида обезболивания
Вид обезболивания |
|
Падение артериального давления в мм |
|
|||||||
|
|
|
во время опыта |
|
|
|
||||
|
|
|
|
|
|
|
||||
Спинномозговая анестезия (v1) |
6 |
5 |
7 |
|
4 |
8 |
|
3 |
8 |
5 |
Эфирный наркоз (v2) |
2 |
3 |
4 |
|
2 |
7 |
|
5 |
4 |
3 |

222 |
Информатика и математика |
Вычисления 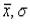 и mx для каждого ряда можно произвести обычным путем, но для упрощения расчетов можно использовать следующую формулу, удобную для применения при малых числах наблюдений:
и mx для каждого ряда можно произвести обычным путем, но для упрощения расчетов можно использовать следующую формулу, удобную для применения при малых числах наблюдений:
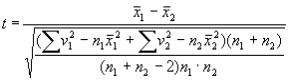 .
.
Упрощение расчетов при использовании этой формулы достигается
тем, что вместо вычисления σ и m ограничиваются определением 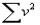 для каждого ряда чисел, что значительно облегчает вычислительную работу (v – отдельные наблюдения, варианты). В данном примере:
для каждого ряда чисел, что значительно облегчает вычислительную работу (v – отдельные наблюдения, варианты). В данном примере:
Σv12= 62+52+72+42 +82 +52 =288 ,
Σv22 = 22 +32 +42 + 22 +72+52 42 +32 =132,
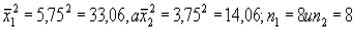 .
.
Подставив все эти значения в приведенную выше формулу, получим:
Оценивая t по данным таблицы Стьюдента, получаем, что при n` =8 +8-2=14 в графе этой таблицы стоит величина 2.14. Следовательно, для
достоверности утверждения неслучайности различия величин 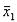 и
и 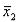 , с вероятностью ошибки не более чем 0, 05 (не более чем 5%) достаточно, чтобы t было не менее чем 2.14. В данном примере t =2,25. Значит, действие двух приведенных видов обезболивания на снижение кровяного давления действительно различно и это различие может считаться статистически доказанным.
, с вероятностью ошибки не более чем 0, 05 (не более чем 5%) достаточно, чтобы t было не менее чем 2.14. В данном примере t =2,25. Значит, действие двух приведенных видов обезболивания на снижение кровяного давления действительно различно и это различие может считаться статистически доказанным.
Оценка достоверности интенсивных коэффициентов заболеваемости при наличии повторных заболеваний. Формула средней ошибки показателя
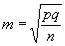 пригодна для оценки показателей только в случаях так называемого альтернативного варьирования, т.е. тогда, когда возможны только два исхода (умер или не умер, заболел данной болезнью или не заболел, привить против данного заболевания или не привит и т.п.).
пригодна для оценки показателей только в случаях так называемого альтернативного варьирования, т.е. тогда, когда возможны только два исхода (умер или не умер, заболел данной болезнью или не заболел, привить против данного заболевания или не привит и т.п.).
Однако характер распределения медико-биологических явлений нередко отличается от нормального. Проводя новые исследования, врачэкспериментатор часто не знает, какому закону варьирования будут следовать результаты, полученные в нескольких опытах, а относительно небольшое число проведенных наблюдений не позволяет ему определить форму распределения. В этих случаях оценку достоверности следует производить с применением так называемых непараметрических критериев.
3. Консультационный курс |
223 |
|
|
ИНФОРМАТИКА И МАТЕМАТИКА
Проблемно-тематический комплекс
Редактор М.В. Егорова
Выпускающий редактор Т.А. Поверина Корректор Г.В. Платова
Лицензия ИД № 00871 от 25.01.00. Подписано в печать 14.09.2011 Формат 70×90 1/16. Усл. печ. л. 13.0. Тираж 2000 экз. Изд. № 2240
Отпечатано в типографии МИЭП 105082, Москва, Рубцовская наб., д. 3, стр. 1
