Лекция_11_С

Для изучения процессов с дискретными состояниями пользуются так называемым графом состояний, в котором состояния системы обозначаются прямоугольниками или кружочками, а возможные переходы из состояния в состояние − ориентированными дугами графа.

1. Рассмотрим марковский процесс с дискретным состоянием и дискретным временем.

Пусть имеется физическая система , которая может находиться в состояниях , , …, , причем переход системы из состояния в состояние осуществляется скачками только в моменты времени , , …, , …, для которых разности равны постоянному числу — шагу, для простоты принимаемому за единицу времени. Такие марковские процессы называются марковскими цепями.

Определение. Вероятностью состояния называется вероятность системы находиться в состоянии после -го шага.

Очевидно, что для каждого шага

.

Будем считать, что вероятности перехода системы из состояния в состояние (они называются переходными вероятностями) одинаковые для всех шагов (такая цепь называется однородной).

Введем так называемую матрицу вероятностей перехода

. (1)

Элементы матрицы неотрицательны, но могут равняться 0: , если переход системы из состояния в состояние невозможен. Сумма элементов любой строки матрицы равна 1. Такие матрицы называются стохастическими.

1. Вероятности перехода из состояния в состояние за шагов определяются матрицей

,

где , откуда следует, что

,

. (2)

2. Теорема Маркова. Если при некотором все элементы матрицы положительны, то существуют такие положительные числа , , …, , что независимо от начального состояния системы имеют место равенства

, причем

. (3)

Вектор называется предельным распределением, а числа — предельными вероятностями состояний.

Предельное распределение можно найти как собственный вектор матрицы ( транспонированная), соответствующий собственному значению .

Пример 2. Задана матрица вероятностей перехода цепи Маркова из состояния в состояние за один шаг. Найти матрицу перехода из состояния в состояние за два шага и вероятность появления цепочки состояний —— за два шага. Выяснить, можно ли к матрице применить теорему Маркова. Если да, найти предельное распределение.

Решение. Матрицу получаем по формуле (2)

.

Вероятность появления цепочки состояний —— за два шага равна , т.е. такой последовательности состояний наблюдаться не может.

Матрица получилась положительной, а это означает, что предельные вероятности существуют. Найдем вектор как собственный вектор матрицы

из матричного уравнения

(4)

при , т.е.

или из системы

Эта система равносильна системе

Решая ее, например методом Жордана-Гаусса, получим

~~, откуда

А с учетом (3)

,

т.е. в стационарном режиме система в среднем всего времени находится в состоянии , — в состоянии и — в состоянии .

2. Рассмотрим марковский процесс с дискретным состоянием и непрерывным временем временем.

Для таких процессов рисуется граф состояний, вершины которого соответствуют состояниям S₀, S₁,…,S_n, а дуги − переходам из одного состояния в другое. Как правило, переход из одного состояния в другое происходит под действием простейшего потока событий с интенсивностью . Граф, дугам которого приписаны интенсивности , называется размеченным.

− вероятность того, что в момент времени система находиться в состоянии .

Для вероятностей имеет место условие нормировки:

(1)

и система уравнений Колмогорова:

(2)

Гдеберётся по всем состояниям , дуги из которых идут в состояния . Во второй сумме берутся все состояния, в которые идут дуги из состояния .

Особый интерес представляет случай, когда система может перейти в стационарный режим.

, − это предельные вероятности, получающиеся при . Их находят из системы:

(3)

Среди системы уравнений (3) одно лишнее (любое), его следует отбросить и добавить условие (1). Доказано, что если число состояний конечно и из каждого состояния можно перейти в любое другое, то предельные вероятности существуют.

Пример:

Найти предельные вероятности для системы, размеченный граф которой имеет вид.

,

,

,

.

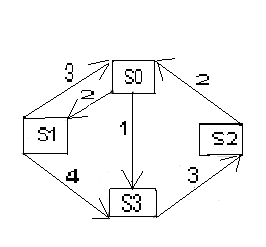
С учетом условия нормировки получаем систему

Отбрасываем третье из уравнений, получаем:

§ 4 Процессы гибели и размножения

описывают изменение численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид

т.к. переход из любого состояния может осуществляться только в состояния с соседними номерами.

,

, т.к. , то остается

,

и далее аналогично

,

…………………..

,

.

Получаем систему

из которой с учетом условия нормировки получаем окончательно

и далее из системы находим , ,…, .

Пример. Дан граф процесса гибели и размножения.

Найдите предельные вероятности состояний.

Решение. ,

,

,

.

Отбрасываем последнее уравнение, добавляем условие нормировки и получаем систему

или

Окончательно

§ 5. Некоторые задачи теории массового обслуживания

Системы массового обслуживания СМО − системы, предназначенные для многократного использования при решении однотипных задач. Каждая система состоит из определенного количества обслуживающих единиц − каналов.

Будем рассматривать многоканальные СМО с отказами (т.е. такие, в которых в случае занятости всех каналов заявка покидает систему необслуженной). Для них введем следующие показатели.

1. интенсивность потока заявок, т.е. среднее количество заявок, поступающих за единицу времени;

2. — абсолютная пропускная способность СМО, т.е. среднее число заявок, рассматриваемых в единицу времени.

3. — относительная пропускная способность, т.е. средняя доля пришедших заявок, обслуживаемых системой.

4. — вероятность отказа, т.е. того, что заявка покинет систему необслуженной.

5. — среднее число занятых каналов для многоканальной системы.

6. — интенсивность обслуживания, т.е. количество заявок, обслуживаемых одним каналом за единицу времени.

7. — среднее время обслуживания, т.е. .

Итак, имеется каналов, на которые поступает поток заявок с интенсивностью . Поток обслуживания каждого канала имеет интенсивность . Найдем предельные вероятности состояний системы и показатели ее эффективности.

Система имеет следующие состояния , , , …, , …, , пронумерованные по числу заявок, находящихся в системе, т.е. — состояние системы, когда в ней находятся заявок (занято каналов).

Граф состояний соответствует процессу гибели и размножения.

Переход в соседнее состояние с большим номером всегда происходит под действием простейшего потока с интенсивностью , а вот переход из состояния в состояние происходит под действием потока интенсивности , так как освободиться может любой из занятых каналов.

Формула для предельной вероятности состояния примет вид

, (1)

где — так называемая интенсивность нагрузки канала, а

, , …, , …, . (2)

Найдем показатели эффективности СМО.

Вероятность отказа системы есть предельная вероятность того, что все каналов будут заняты, т.е.

.

Относительная пропускная способность — вероятность того, что заявка будет обслужена

.

Абсолютная пропускная способность

.

Среднее число занятых каналов , т.е. математическое ожидание числа занятых каналов

или иначе .

Далее разбирайте задачи к практическому занятию и используйте методички (см. список литературы).