Министерство образования и науки РФ

«Красноярский государственный педагогический университет имени В.П. Астафьева»

Филиал КГПУ имени В.П. Астафьева в городе Канске.

Сущность теории Рамсея. Теорема Рамсея. Числа Рамсея.

Реферат   

Выполнил: Захаров А.А.

Проверил: Кондрашов А.М.

Канск, 2012

Содержание

1. Сущность теории Рамсея.

2. Теорема Рамсея.

3. Числа Рамсея.

4. Приложения теоремы Рамсея.

5. Теорема Ван дер Вардена. 

 

Сущность теории Рамсея.

Талантливый математик Фрэнк Пламптон Рамсей доказал, что полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высоко упорядоченную структуру.

Фактически теория Рамсея утверждает, что любая структура обязательно содержит упорядоченную подструктуру. Как впервые провозгласил около четверти века назад умерший недавно американский математик Теодор С.Моцкин, из теории Рамсея следует, что полный беспорядок невозможен.

Специалисты по теории Рамсея стараются вычислить, сколь велико должно быть множество звёзд, чисел или каких-либо объектов, чтобы можно было гарантировать существование определённой желаемой подструктуры. На решение таких задач часто требуются десятилетия, и поддаются они только при самом изобретательном и тонком рассуждении. Пытаясь найти решения поставленной задачи, специалисты по теории Рамсея помогают тем самым инженерам в построении более совершенных сетей коммуникации и систем передачи и поиска информации. Они также открыли некоторые математические методы, которые пригодятся учёным следующего столетия. Возможно, самое важное заключается в том, что теория Рамсея исследует основополагающую структуру математики, т.е. структуру, пронизывающую всю Вселенную.

Теорема Рамсея.

Прототипом «рамсеевской теоремы» послужила оригинальная теорема самого Рамсея. Первоначально доказанная в связи с некоторыми вопросами разрешимости в логике, она оказалась тем плодотворным зерном, из которого выросла большая часть рамсеевской теории.

Прежде всего рассмотрим (как и Рамсей) бесконечный случай.

Теорема Рамсея (бесконечный случай).Для всех k, r   и произвольного r-раскрашивания : множества всехk –элементных подмножеств множества  всегда найдется бесконечное подмножество S   со всеми своими k-элементными подмножествами, имеющими один и тот же цвет.

Теорема Рамсея (конечный случай). Для всех k, l, r   найдется n(k, l, r)  , такое, что если n  n(k, l, r) и : есть произвольноеr-раскрашивание всех k-подмножеств из , то некотороеl-подмножество из имеет всеk-подмножества одного и того же цвета.

Наименьшие возможные значения чисел n(k, l, r), известные как числа Рамсея, обозначаются R(k, l, r).

Числа Рамсея.

Число Рамсея R(k, m) это наименьшее число n такое, что в любом графе с n вершинами, найдутся либо k попарно смежных, либо m попарно несмежных.

Теорема Рамсея гарантирует существование чисел Рамсея для любых k и m. Таким образом можно говорить о содержании в бесконечном графе высокоорганизованной структуры любой сложности. Но об этом позже (быть может). А пока хочется остановиться на числах Рамсея. Для удобства перефразируем определение: Число Рамсея R(k, m) это наименьшее число n такое, что в любом полном графе с n вершинами, ребра которого раскрашены в красный и синий цвета, найдется либо подграф с k вершинами, все ребра которого окрашены в красный цвет, либо подграф с m вершинами, все ребра которого окрашены в синий цвет.  Чтобы понять сложность вычисления чисел Рамсея, то следует отметить что число R(5, 5) до сих пор не найдено. Можно заметить три очевидных факта, касающихся чисел Рамсея:

1. R(k, m) = R(m, k)

2. R(1, m) = 1

3. R(2, m) = m

Остальные числа вычисляются индивидуально. Задача о вычислении R(3, 3) известна как "задача о вечеринке": среди любых 6 человек найдется либо 3 попарно знакомых, либо 3 попарно незнакомых. Другими словами R(3, 3) <= 6. Доказательство строится следующим образом (в терминах второго приведенного определения): Изобразим граф с шестью вершинами и возьмем одну из них - A: 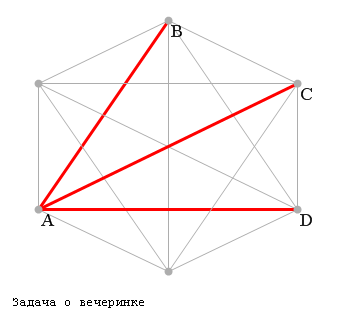Вершина A соединена с пятью другими вершинами (красными и синими ребрами). Без ограничения общности можно считать, что она соединена красными ребрами по крайней мере с тремя вершинами - B, C, D. Далее, если одно из ребер BC, CD, BD красное (например BC), то имеем красный треугольник (ABC). Если же все они синие, то BCD - синий треугольник. Конец доказательства.  Имея в виду то, что число 5 не удовлетворяет требованиям задачи, получаем R(3, 3) = 6. Дальше докажем, что R(3, 4) = 9. Сначала установим, что R(3, 4) > 8. 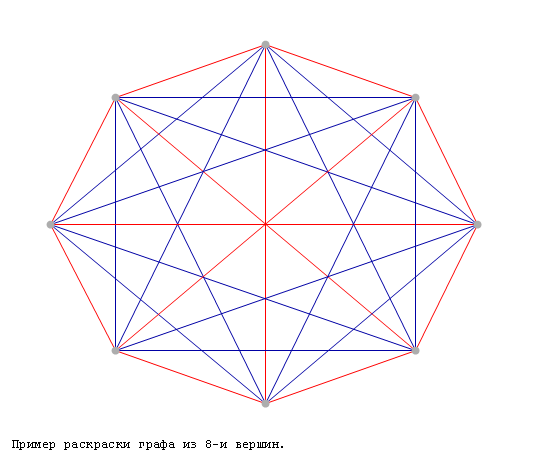Для этого достаточно привести пример раскраски графа из 8 вершин, не содержащего красных треугольников и полных синих подграфов из 4 вершин: Осталось доказать, что полный граф из 9 вершин так раскрасить нельзя. Допустим, такая раскраска возможна. Будем рассуждать как в предыдущем доказательстве. Возьмем одну из вершин (A), с остальными вершинами она соединена 8 ребрами. Пусть k из них покрашены в красный цвет, а остальные 8-k - в синий. Если k >= R(2, 4) = 4, то A соединена красными ребрами хотя бы с четырьмя вершинами (B, C, D, E). Если две из этих вершин соединены красным ребром, то сразу имеем красный треугольник, а если нет, то BCDE - полный синий граф из четырех вершин. Значит k < 4. Аналогичным образом 8-k < R(3, 3) = 6. Из этих двух неравенств имеем (k < 4) && (k > 2) => k = 3. Так как наши рассуждения не зависят от выбора вершины, то можно утверждать, что из любой вершины выходит ровно три красных ребра, а значит общее число красных ребер в графе равно 3 * 9 / 2. Но это число не является целым, мы пришли к противоречию. Следовательно требуемой раскраски не существует и R(3, 4) = 9. Конец доказательства. P.S. Данное доказательство пока не слишком сложное, но все же сложнее вычисления R(3, 3). Для больших параметров доказательства значительно усложняются. Дело в том, что не существует системного метода поиска чисел Рамсея (есть только грубые оценки), а с ростом параметров начинается очень обширное комбинаторное многообразие, не позволяющее найти решение даже компьютеру...

P.P.S. Практического применения чисел Рамсея нет, но в процессе их поиска было разработано масса полезного инструментария как в теории графов, так и в смежных областях.