
идз4
.pdf
Теория Вероятностей и математическая статистика
Индвидуальное задание №4.
In[1]: |
import numpy as np |
|
|
import matplotlib.pyplot as plt |
|
|
import pandas as pd |
|
|
import scipy.stats as sp |
|
|
from scipy.optimize |
import minimize |
|
from scipy.special import nctdtrit |
|
|
import math |
|
|
from decimal import |
Decimal as dec |
|
from decimal import |
getcontext |
|
%matplotlib inline |
|
|
|
|
Задание 1
В результате эксперимента получены данные, приведённые в таблице:
2, 9, 11, 19, 0, 2, 5, 0, 9, 0, 0, 6, 4, 2, 2, 2, 2, 1, 4, 1, 1, 6, 3, 0, 3, 2, 6, 7, 1, 17, 0, 0, 1, 9, 7, 10, 4, 1, 13, 1, 3, 3, 0, 3, 2, 1, 3, 8, 11, 2
In[49]: d = np.array([2, 9, 11, 19, 0, 2, 5, 0, 9, 0, 0, 6, 4, 2, 2, 2, 2, 1, 4, 1, 1, 6, 3, 0, 3, 2, 6, 7, 1, 17, 0, 0, 1, 9, 7, 10, 4, 1, 13, 1, 3, 3, 0, 3, 2, 1, 3, 8, 11, 2])
alpha1 = 0.02 a = 2.21
b = 8.47 lam0 = 6 lam1 = 4
n = len(d)
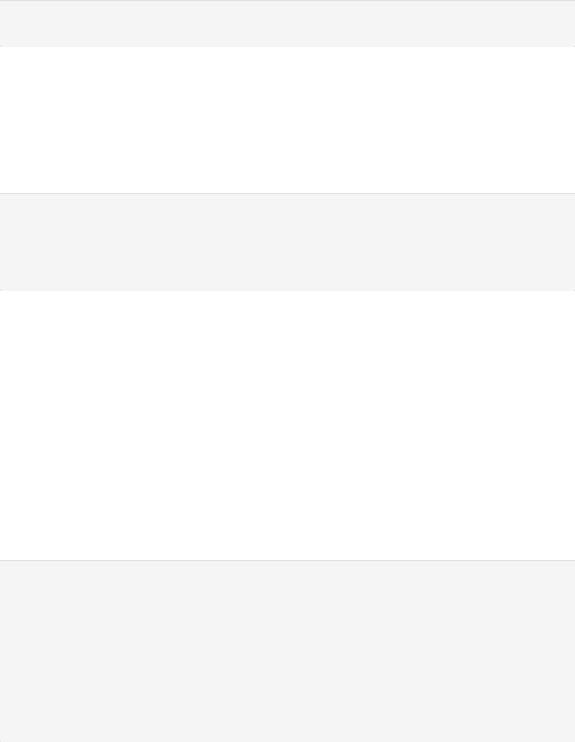
a) Построить вариационный ряд, эмпирическую функцию распределения и гистограмму частот
Решение:
Построим вариационный ряд:
In [50]: d.sort()
print("Вариационный ряд: ", *d)
Вариационный ряд: 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 5 6 6 6 7 7 8 9 9 9 10 11 11 13 17 19
Вариационный ряд: 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 6, 6, 6, 7, 7, 8, 9, 9, 9, 10, 11, 11, 13, 17, 19
Найдём эмпирическую функцию распределения:
In [51]: '''
Подсчёт количества уникальных элементов
'''
d_unique, counts = np.unique(d, return_counts=True) print(np.asarray((d_unique, counts)).T)
[[ 0 8] [ 1 8] [ 2 9] [ 3 6] [ 4 3] [ 5 1] [ 6 3] [ 7 2] [ 8 1] [ 9 3] [10 1] [11 2] [13 1] [17 1] [19 1]]
In [52]: sum_p = 0 distr_func = {} prob_list = []
getcontext().prec = 2
for i in range(len(counts)): prob = dec(counts[i] / n) prob_list.append(float(prob))
distr_func.update({d_unique[i]: float(prob + sum_p)}) sum_p += prob
distr_func

Out[52]: {0: 0.16, 1: 0.32, 2: 0.5, 3: 0.62, 4: 0.68, 5: 0.7, 6: 0.76, 7: 0.8, 8: 0.82, 9: 0.88, 10: 0.9, 11: 0.94, 13: 0.96, 17: 0.98, 19: 1.0}
Тогда:
In [53]: distr_func.update({-20: 0}) distr_func.update({20: 1}) plt.xlim(-5, 19)
plt.xticks([x for x in range(-5, 21)]) plt.grid()
d_un = [-20, *sorted(list(set(d))), 20] for i in range(0, len(d_unique)):
plt.hlines(y=distr_func[d_un[i]], xmin=d_un[i], xmax=d_un[i+1], color='b') plt.plot(d_un[i], distr_func[d_un[i]], marker='o', color='b')
plt.show()
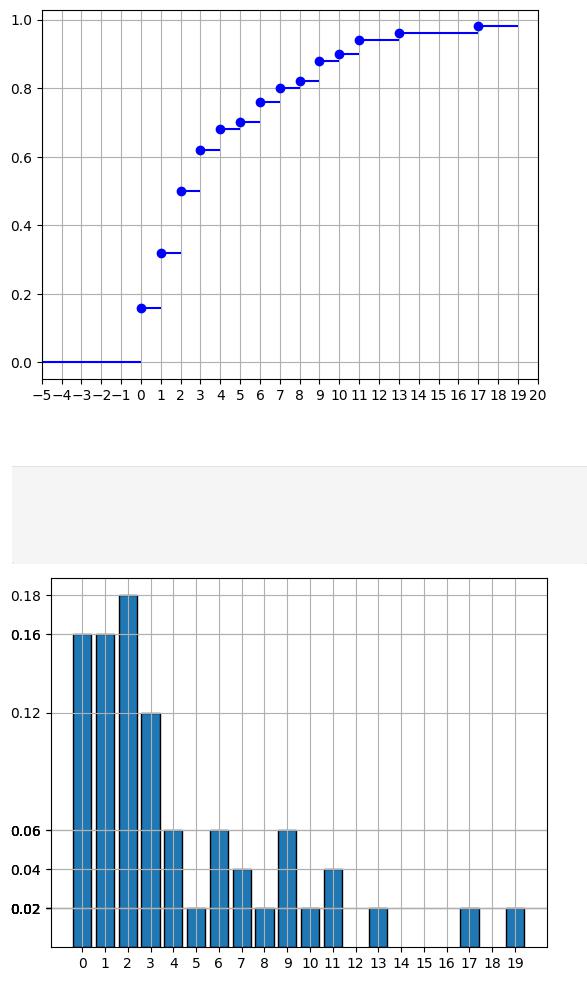
Гистограмма частот:
In [54]: plt.bar(d_unique, prob_list, edgecolor='black') plt.xticks(np.arange(0, 20)) plt.yticks(prob_list)
plt.grid() plt.show()
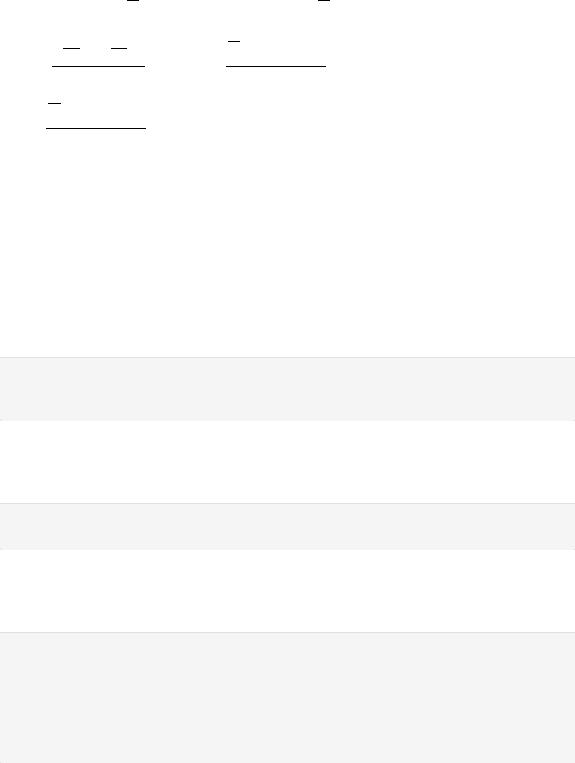
b) Вычислить выборочные аналоги |
|
следующих числовых характеристик: (i) |
|
математического ожидания, (ii) |
|
дисперсии, (iii) медианы, (iv) |
|
ассиметрии, (v) эксцесса, (vi) |
|
вероятности |
9im |
Ответ:
Вычислим выборочное математическое ожидание:
In [8]: |
Ex |
= d.mean() # мат ожидание |
|
Ex |
|
|
|
|
Out[8]: 4.18
Вычислим выборочную дисперсию и СКО:
In [9]: Dx = round(d.var(), 4) # дисперсия sigma = math.sqrt(Dx)
Dx, sigma
Out[9]: (19.4276, 4.407675124144247)
Вычислим медиану:
In [10]: median = np.median(d) median
Out[10]: 2.5
Вычислим коэффициент асимметрии:
In [11]: sum_3_d = 0 for x in d:
sum_3_d += (x - Ex) ** 3
sum_3_d /= n
A = sum_3_d / (sigma ** 3) A

Out[11]: |
1.4924961375534034 |
|
|
|
|
||
|
Вычислим эксцесс: |
||||||
|
|
|
|
|
|
|
|
In [12]: |
sum_4_d = 0 |
||||||
|
for x in d: |
||||||
|
sum_4_d += (x - Ex) ** 4 |
||||||
|
sum_4_d /= n |
||||||
|
e = (sum_4_d / (sigma ** 4)) - 3 |
||||||
|
e |
||||||
|
|
|
|
|
|
|
|
Out[12]: |
1.8879417372566376 |
|
|
|
|
||
|
c) В предположении, что исходные |
||||||
|
наблюдения являются выборкой из |
||||||
|
распределения Пуассона, построить |
||||||
|
оценку максимального правдоподобия |
||||||
|
параметра , а также оценку по |
||||||
|
методу моментов |
||||||
|
Метод максимального правдоподобия: |
||||||
|
Распределение Пуассона: |
||||||
|
|
|
|
|
|
|
|
|
Тогда функция правдоподобия: |
||||||
|
|
|
|
|
|
||
|
Тогда логарифмическая функция правдоподобия: |
||||||
|
Тогда: |
||||||
Проверим, что - точка максимума:
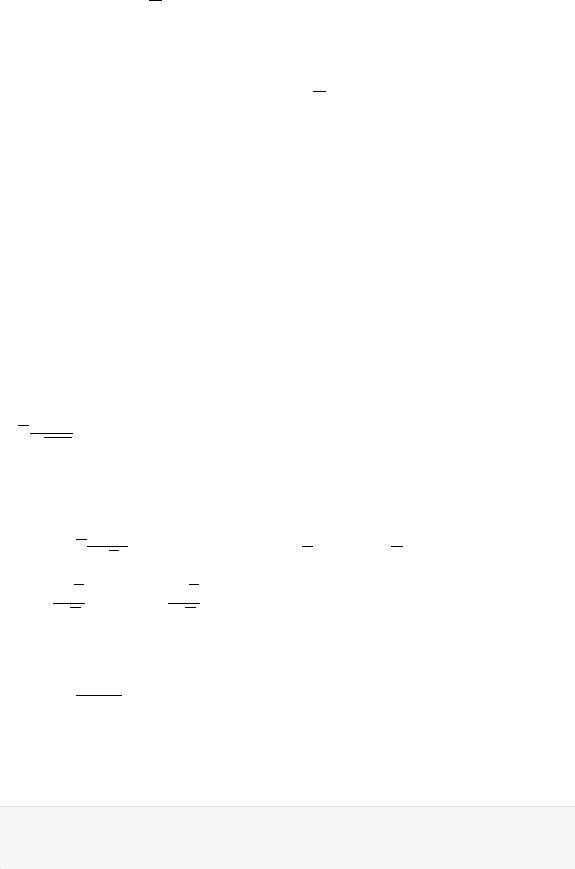
Т.е. - точка максимума.
Метод моментов:
Теоретический момент первого порядка в распределении Пуассона:
Эмпирический момент первого порядка:
Тогда:
d) Построить асимптотический доверительный интервал уровня значимости для параметра на
базе оценки максимального правдоподобия
По ЦПТ:
Т.к. в распределении Пуассона |
и по методу максимального |
|
правдоподобия |
: |
|
\
Т.к. то:
Тогда:
In [13]: left_border = Ex - (2.32 * math.sqrt(Ex) / math.sqrt(n)) right_border = Ex + (2.32 * math.sqrt(Ex) / math.sqrt(n)) [round(left_border, 4), round(right_border,4)]

Out[13]: [3.5092, 4.8508]
e) Используя гистограмму частот, построить критерий значимости
проверки простой гипотезы согласия с распределением Пуассона с параметром . Проверить гипотезу на
уровне значимости . Вычислить
наибольшее значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Т.к. Гипотеза
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline
$i$ & $I_i$ & $n_i$ & $p_i$ & $np_i$ & $n_i-np_i$ & $\cfrac{(n_i-np_i)^2}{np_i}$ \\ \hline
$1$ & $( - \infty; 0]$ & $8$ & $ 0.0025$ & $ 0.125 $ & $ 7.875 $ & $ 496.125 $ \\ \hline
$2$ & $(0; 1]$ & $8 & $0.0149 $ & $ 0.745 $ & $ 7.225 $ & $ 70.651 $ \\ \hline
$3$ & $(1; 2]$ & $9$ & $ 0.0446 $ & $ 2.23 $ & $ 6.77 $ & $ 20.5529 $ \\ \hline
$4$ & $(2; 4]$ & $9$ & $ 0.2231 $ & $ 11.155 $ & $ -2.155 $ & $ 0.4163 $ \\ \hline
$5$ & $(4; 8]$ & $7$ & $ 0.5622$ & $ 28.11$ & $ -21.11 $ & $ 15.8532 $ \\ \hline
$6$ & $(8; +\infty]$ & $9$ & $ 0.1528$ & $ 7.64$ & $ 1.36 $ & $ 0.2421$ \\ \hline
$\sum $ & $ $ & $50$ & $ 1$ & $ $ & $ $ & $ 603.8405 $ \\ \hline
\end{tabular}
In [14]: |
I |
= |
[(-math.inf, 0), (0, 1), (1, 2), (2, 4), (4, 8), (8, math.inf)] |
|
# |
I |
= [(-math.inf, 4), (4, 8), (8, math.inf)] |
|
n_i = [8, 8, 9, 9, 7, 9] |
||
|
p_i |
= [] |
|
|
np_i = [] |
||
|
|
|
|
n_i_np_i = [] res = []
for i in I:
p_i.append(round(sp.poisson.cdf(i[1], lam0) - sp.poisson.cdf(i[0], lam0), 4)
for i in p_i: np_i.append(round(i*n, 4))
for i in range(len(n_i)): n_i_np_i.append(round(n_i[i] - np_i[i], 4))
for i in range(len(n_i)):
res.append(round((n_i_np_i[i] ** 2) / np_i[i] , 4))
res, sum(res)
Out[14]: ([496.125, 70.651, 20.5529, 0.4163, 15.8532, 0.2421], 603.8405)
Получаем
Проверим гипотезу на уровне значимости |
: |
Тогда для
Следовательно нулевую гипотезу мы отвергаем. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
In [15]: 1 - sp.chi2.cdf(sum(res), 4)
Out[15]: 0.0
f) Построить критерий значимости
проверки сложной гипотезы согласия с геометрическим распределением. Проверить гипотезу на уровне значимости . Вычислить наибольшее
значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Минимизируем функцию для :
In [16]: def chi_squared(x): p_min = [] res_min = 0
for i in I:
p_min.append(sp.poisson.cdf(i[1], x) - sp.poisson.cdf(i[0], x))
for i in range(len(n_i)):
res_min += ((n_i[i]-n*p_min[i])**2)/(n*p_min[i])
return res_min
theta_minimized = float(minimize(chi_squared, lam0).x) print(theta_minimized, chi_squared(theta_minimized))
4.067488240872976 |
130.59256800912323 |
|
Тогда |
при |
Проверим гипотезу на уровне |
значимости |
|
: |
Тогда для |
|
|
Следовательно нулевую гипотезу мы отвергаем. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
In [17]: 1 - sp.chi2.cdf(chi_squared(theta_minimized), 4)
Out[17]: 0.0
g) В пунктах (c)-(f) заменить семейство распределений Пуассона на семейство геометрических распределений
g.c) Построить оценку максимального правдоподобия параметра , а также оценку по методу моментов
Функция правдоподобия:
Тогда логарифмическая функция правдоподобия:
