
идз4
.pdf
Тогда:
Проверим, что - точка максимума:
т к
справедливо при Т.е. - точка максимума.
Метод моментов:
Тогда |
: |
g.d) Построить асимптотический доверительный интервал уровня значимости для параметра на
базе оценки максимального правдоподобия
По лемме Фишера:
Тогда:

Где
Тогда:
In [18]: |
x_alpha = nctdtrit(n |
- 1, 0, 0.99) |
|||
|
lb |
= |
Ex |
- (x_alpha * |
sigma)/math.sqrt(n) |
|
rb |
= |
Ex |
+ (x_alpha * |
sigma)/math.sqrt(n) |
|
[round(lb, 4), round(rb, 4)] |
||||
|
|
|
|
|
|
Out[18]: |
[2.6809, 5.6791] |
|
|||
g.e) Используя гистограмму частот, построить критерий значимости
проверки простой гипотезы согласия с распределением Пуассона с параметром . Проверить гипотезу на
уровне значимости . Вычислить
наибольшее значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Т.к. Гипотеза

\begin{tabular}{|c|c|c|c|c|c|c|}
\hline
$i$ & $I_i$ & $n_i$ & $p_i$ & $np_i$ & $n_i-np_i$ & $\cfrac{(n_i-np_i)^2}{np_i}$ \\ \hline
$1$ & $( - \infty; 0]$ & $8$ & $ 0.2 $ & $ 10 $ & $ -2 $ & $ 0.4 $ \\ \hline
$2$ & $(0; 1]$ & $8 & $ 0.16 $ & $ 8 $ & $ 0 $ & $ 0 $ \\
\hline
$3$ & $(1; 2]$ & $9$ & $ 0.128 $ & $ 6.4 $ & $ 2.6 $ & $ 1.0563 $ \\ \hline
$4$ & $(2; 4]$ & $9$ & $ 0.1843 $ & $ 9.215 $ & $ -0.215 $ & $ 0.005 $ \\ \hline
$5$ & $(4; 8]$ & $7$ & $ 0.1935 & $ 9.675$ & $ -2.675 $ & $ 0.7396 $ \\ \hline
$6$ & $(8; +\infty]$ & $9$ & $ 0.1342 & $ 7.64$ & $ 2.29 $ & $ 0.7815$ \\ \hline
$\sum $ & $ $ & $50$ & $ 1$ & $ $ & $ $ & $ 2.9824 $ \\ \hline
\end{tabular}
In [19]: def geom_distr(x, lam): res_g = 0
for i in range(0, x + 1):
res_g += (lam**i)/((lam+1)**(i+1)) return res_g
I = [(-math.inf, 0), (0, 1), (1, 2), (2, 4), (4, 8), (8, math.inf)]
# I = [(-math.inf, 4), (4, 8), (8, math.inf)] n_i = [8, 8, 9, 9, 7, 9]
p_i = [] np_i = []
n_i_np_i = [] res = []
p_i.append(geom_distr(0, lam1)) for i in range(1, len(n_i) - 1):
p_i.append(round(geom_distr(I[i][1], lam1) - geom_distr(I[i][0], lam1), 4)) p_i.append(round(geom_distr(10000, lam1) - geom_distr(8, lam1), 4))
for i in p_i: np_i.append(round(i*n, 4))
for i in range(len(n_i)): n_i_np_i.append(round(n_i[i] - np_i[i], 4))
for i in range(len(n_i)):
res.append(round((n_i_np_i[i] ** 2) / np_i[i] , 4))
res, sum(res)
Out[19]: ([0.4, 0.0, 1.0563, 0.005, 0.7396, 0.7815], 2.9823999999999997)
Получаем
Проверим гипотезу на уровне значимости |
: |
Тогда для

Следовательно нулевую гипотезу нельзя отвергнуть. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
In [20]: 1 - sp.chi2.cdf(sum(res), 4)
Out[20]: 0.5607750255296444
g.f) Построить критерий значимости
проверки сложной гипотезы согласия с геометрическим распределением. Проверить гипотезу на уровне значимости . Вычислить наибольшее
значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Минимизируем функцию для :
In [21]: |
def chi_squared(x): |
|
|
p_min |
= geom_distr(0, x) |
|
res_f |
= ((n_i[0]-n*p_min)**2)/(n*p_min) |
|
for i |
in range(1, len(n_i) - 1): |
|
|
p_min = geom_distr(I[i][1], x) - geom_distr(I[i][0], x) |
|
|
res_f += ((n_i[i]-n*p_min)**2)/(n*p_min) |
|
p_min |
= geom_distr(100, x) - geom_distr(8, x) |
|
res_f |
+= ((n_i[5]-n*p_min)**2)/(n*p_min) |
|
return res_f |
|
|
theta_minimized = float(minimize(chi_squared, lam1).x) |
|
|
print(theta_minimized, chi_squared(theta_minimized)) |
|
|
|
|
4.41933150671743 2.592767686345728 |
||
Тогда |
при |
Проверим гипотезу на уровне значимости |
|
: |
|
Тогда для |
|
|
Следовательно нулевую гипотезу нельзя отвергнуть. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
In [22]: 1 - sp.chi2.cdf(chi_squared(theta_minimized), 4)
Out[22]: 0.6281048300545914
Задание 2
В результате эксперимента получены данные, приведённые в таблице:
0.420, 0.122, 0.792, 0.080, 0.382, 0.849, 0.600, 0.002, 0.998, 0.003, 0.328, 0.211, 0.184, 1.201, 0.990, 0.025, 0.072, 0.183, 0.512, 0.190, 1.054, 0.043, 1.157, 0.030, 2.014, 0.024, 0.025, 0.669, 1.130, 0.229, 0.036, 0.237, 3.860, 0.427, 0.000, 0.413, 1.775, 0.011, 0.075, 0.774, 0.005, 0.015, 1.347, 0.103, 0.036, 0.028, 0.377, 0.043, 2.346, 0.121
a) Построить вариационный ряд, эмпирическую функцию распределения, гистограмму и полигон частот с шагом h
In [23]: d2 = np.array([0.420, 0.122, 0.792, 0.080, 0.382, 0.849, 0.600, 0.002, 0.998, 0.
alpha2 = 0.2 cv = 0
dv = 1.21 lam02 = 0.48 lam12 = 1.43 h = 0.2
n2 = len(d)
Вариационный ряд:
In [24]: d2.sort()
print("Вариационный ряд: ", *d2)
Вариационный ряд: 0.0 0.002 0.003 0.005 0.011 0.015 0.024 0.025 0.025 0.028 0.03 0.036 0.036 0.043 0.043 0.072 0.075 0.08 0.103 0.121 0.122 0.183 0.184 0.19 0.211 0.229 0.237 0.328 0.377 0.382 0.413 0.42 0.427 0.512 0.6 0.669 0.774 0.792 0.849 0.99 0.998 1.054 1.13 1.157 1.201 1.347 1.775 2.014 2.346 3.86
In [25]: distr_func2 = {}
for i in range(0, len(d2)): distr_func2.update({d2[i]: float((i + 1) / n2)})
distr_func2

Out[25]: {0.0: 0.02, 0.002: 0.04, 0.003: 0.06, 0.005: 0.08, 0.011: 0.1, 0.015: 0.12, 0.024: 0.14, 0.025: 0.18, 0.028: 0.2, 0.03: 0.22, 0.036: 0.26, 0.043: 0.3, 0.072: 0.32, 0.075: 0.34, 0.08: 0.36, 0.103: 0.38, 0.121: 0.4, 0.122: 0.42, 0.183: 0.44, 0.184: 0.46, 0.19: 0.48, 0.211: 0.5, 0.229: 0.52, 0.237: 0.54, 0.328: 0.56, 0.377: 0.58, 0.382: 0.6, 0.413: 0.62, 0.42: 0.64, 0.427: 0.66, 0.512: 0.68, 0.6: 0.7, 0.669: 0.72, 0.774: 0.74, 0.792: 0.76, 0.849: 0.78, 0.99: 0.8, 0.998: 0.82, 1.054: 0.84, 1.13: 0.86, 1.157: 0.88, 1.201: 0.9, 1.347: 0.92, 1.775: 0.94, 2.014: 0.96, 2.346: 0.98, 3.86: 1.0}
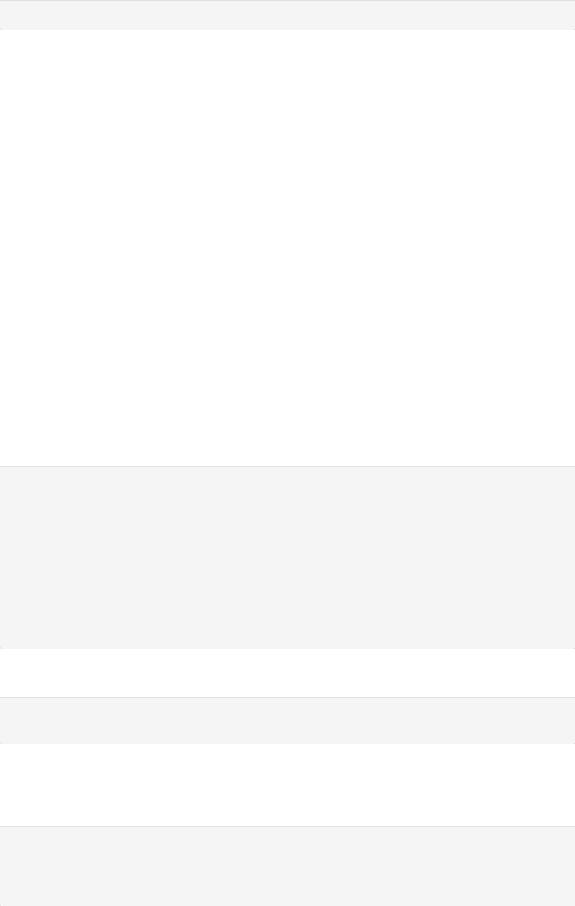
Тогда функция распределения:
In [26]: distr_func2.update({-20: 0}) distr_func2.update({51: 1}) plt.xlim(-2, 7)
plt.xticks([x for x in range(-1, 7)]) plt.grid()
d2_un = [-20, *sorted(list(set(d2))), 51] for i in range(0, 48):
plt.hlines(y=distr_func2[d2_un[i]], xmin=d2_un[i], xmax=d2_un[i+1], color=' plt.plot(d2_un[i], distr_func2[d2_un[i]], marker='o', color='b')
plt.show()
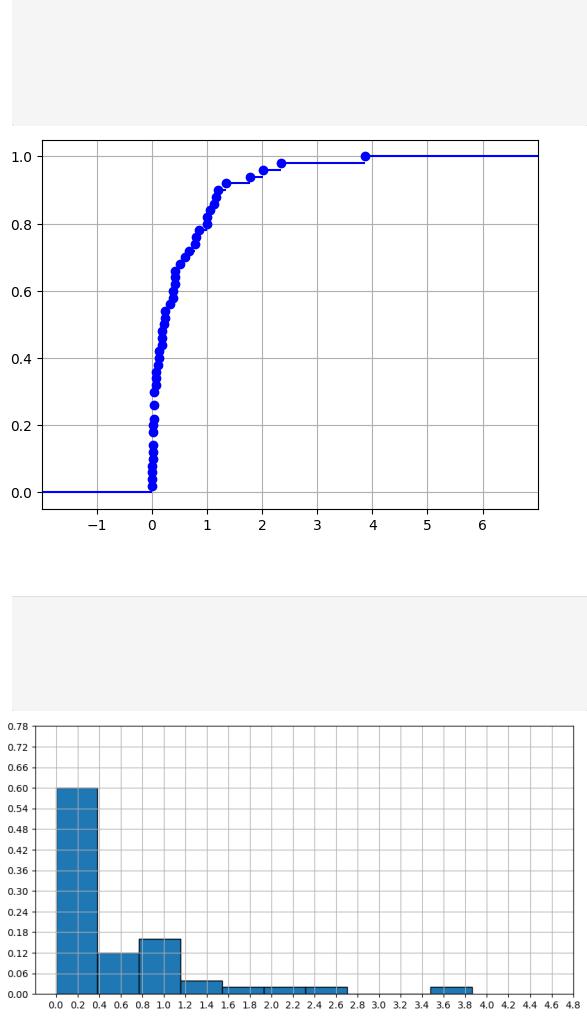
Построим гистограмму частот:
In [27]: plt.figure(figsize=(10, 5))
plt.hist(d2, weights=np.ones_like(d2)/len(d2), bins=10, edgecolor='black') plt.xticks(np.arange(0.000, 5.000, 0.2))
plt.yticks([i / 50 for i in range(0, 41, 3)]) plt.grid()
plt.show()
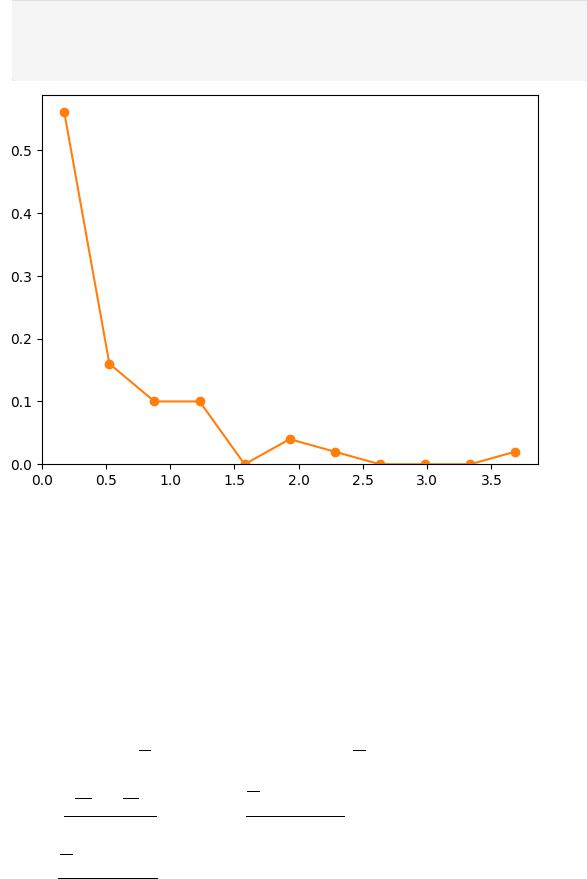
Построим полигон частот с шагом h:
In [28]: counts, bins, bars = plt.hist(d2, weights=np.ones_like(d2)/len(d2), bins=11 ,rwi bin_center = (bins[1] - bins[0])/2
plt.plot(bins[:-1]+bin_center, counts, 'o-') plt.show()
b) Вычислить выборочные аналоги следующих числовых характеристик: (i) математического ожидания, (ii) дисперсии, (iii) медианы, (iv) ассиметрии, (v) эксцесса, (vi) вероятности
Ответ:
Вычислим математическое ожидание:
In [29]: |
Ex = d2.mean() |
|
Ex |
|
|
Out[29]: |
0.53096 |
|
Вычислим дисперсию: |
|
|
In [30]: |
Dx = d2.var() |
|
sigma2 = math.sqrt(Dx) |
|
Dx |
|
|
Out[30]: |
0.5347894784 |
|
Вычислим медиану: |
|
|
In [31]: |
Me = np.median(d2) |
|
Me |
|
|
Out[31]: |
0.22 |
|
Вычислим коэффициент асимметрии: |
|
|
In [32]: |
sum_3_d = 0 |
|
for x in d2: |
|
sum_3_d += (x - Ex) ** 3 |
|
sum_3_d /= n2 |
|
A = sum_3_d / (sigma2 ** 3) |
|
A |
|
|
Out[32]: |
2.406680661409086 |
|
Вычислим эксцессу: |
|
|
In [33]: |
sum_4_d = 0 |
|
for x in d2: |
|
sum_4_d += (x - Ex) ** 4 |
|
sum_4_d /= n2 |
|
e = (sum_4_d / (sigma2 ** 4)) - 3 |
|
e |
|
|
Out[33]: |
7.022713710643044 |
|
c) В предположении, что исходные |
|
наблюдения являются выборкой из |
|
показательного распределения, |
|
построить оценку максимального |
|
правдоподобия параметра , а также |
|
оценку по методу моментов |
Метод максимального правдоподобия:
Показательное распределение:
Тогда функция правдоподобия:
Тогда логарифмическая функция правдоподобия:
Тогда:
Проверим, что - точка максимума:
Т.е. - точка максимума.
Метод моментов:
Теоретический момент первого порядка в показательном распределении:
Эмпирический момент первого порядка:
Тогда:
d) Построить асимптотический |
|
доверительный интервал уровня |
|
значимости |
для параметра на |
