
идз4
.pdf
базе оценки максимального
правдоподобия
По ЦПТ:
Т.к. в показательном распределении |
|
и по методу максимального |
||
|
||||
правдоподобия |
|
: |
|
|
|
|
|
||
\
Т.к. то:
Тогда:
In [215 … |
left_border = 1 / (Ex + |
((1.28 * Ex) / math.sqrt(n))) |
|
right_border = 1 / (Ex - ((1.28 * Ex) / math.sqrt(n))) |
|
|
[round(left_border, 4), |
round(right_border,4)] |
|
|
|
Out[215]: |
[1.5947, 2.2997] |
|
e) Используя гистограмму частот, построить критерий значимости
проверки простой гипотезы согласия с показательным распределением с параметром . Проверить гипотезу на
уровне значимости . Вычислить
наибольшее значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Т.к. Гипотеза
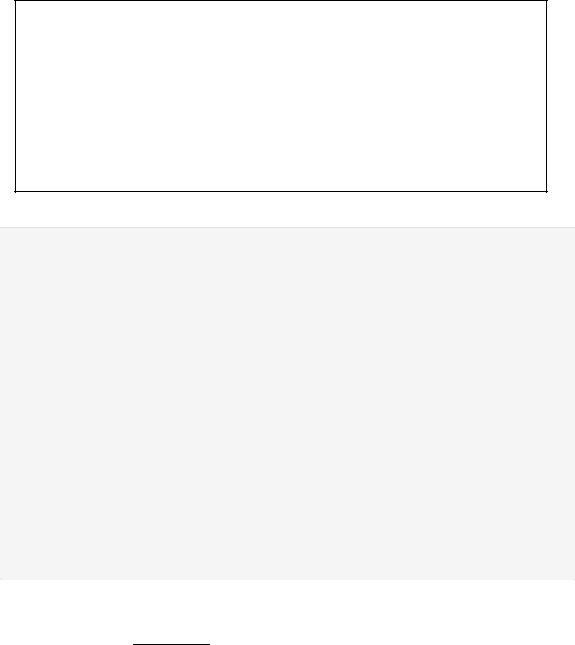
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline
$i$ & $I_i$ & $n_i$ & $p_i$ & $np_i$ & $n_i-np_i$ & $\cfrac{(n_i-np_i)^2}{np_i}$ \\ \hline
$1$ & $( - \infty; 1]$ & $41$ & $ 0.4055$ & $ 20.275 $ & $ 20.725 $ & $ 21.185 $ \\ \hline
$2$ & $(1; +\infty]$ & $9$ & $ 0.5945$ & $ 29.725$ & $ -20.725 $ & $ 14.45 $ \\ \hline
$\sum $ & $ $ & $50$ & $ 1$ & $ $ & $ $ & $ 35.635 $ \\ \hline
\end{tabular}
In [34]: I = |
[[-math.inf, 1], [1, +math.inf]] |
|
n_i |
= [41, 9] |
|
p_i |
= [] |
|
np_i = [] |
|
|
n_i_np_i |
= [] |
|
res |
= [] |
|
for |
i in |
I: |
|
p_i.append(round(sp.expon.cdf(i[1], lam02) - sp.expon.cdf(i[0], lam02), 4)) |
|
for |
i in |
p_i: |
|
np_i.append(round(i*n, 4)) |
|
for |
i in |
range(len(n_i)): |
|
n_i_np_i.append(round(n_i[i] - np_i[i], 4)) |
|
for |
i in |
range(len(n_i)): |
|
res.append(round((n_i_np_i[i] ** 2) / np_i[i] , 4)) |
|
res, sum(res)
Out[34]: ([21.185, 14.45], 35.635)
Получаем
Проверим гипотезу на уровне значимости |
: |
Тогда для
Следовательно нулевую гипотезу мы отвергаем. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
f) Построить критерий значимости
проверки сложной гипотезы согласия с показательным распределением. Проверить гипотезу на уровне значимости . Вычислить наибольшее
значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Минимизируем функцию для :
In [35]: def chi_squared(x): res = 0
for i in range(2):
res_p = sp.expon.cdf(I[i][1], x) - sp.expon.cdf(I[i][0], x) res += ((n_i[i]-n*res_p)**2)/(n*res_p)
return res
theta_minimized = float(minimize(chi_squared, lam02).x) print(theta_minimized, chi_squared(theta_minimized))
-0.7147983607185363 4.9820199798920003e-14
Тогда |
при |
Проверим гипотезу на уровне значимости |
|
: |
|
Тогда для |
|
|
Следовательно нулевую гипотезу нельзя отвергнуть. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
In [36]: 1 - sp.chi2.cdf(chi_squared(theta_minimized), 1)
Out[36]: 0.9999998219086632
g) В пунктах (c)-(f) заменить семейство показательных распределений на семейство гамма-распределений с

плотностями
(использовать таблицу распределений
)
g.c) В предположении, что исходные наблюдения являются выборкой из показательного распределения, построить оценку максимального правдоподобия параметра , а также оценку по методу моментов
Метод максимального правдоподобия:
Гамма-распределение:
Тогда функция правдоподобия:
Тогда логарифмическая функция правдоподобия:
Тогда:
Получаем:
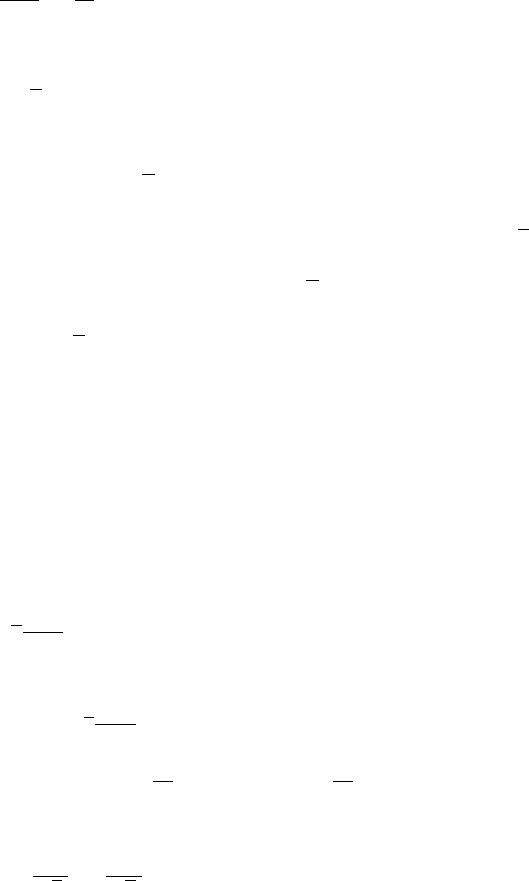
Проверим, что - точка максимума:
Т.е. - точка максимума.
Метод моментов:
Теоретический момент первого порядка в показательном распределении:
Эмпирический момент первого порядка:
Тогда:
g.d) Построить асимптотический доверительный интервал уровня значимости для параметра на
базе оценки максимального правдоподобия
По лемме Фишера:
Тогда:
Где Тогда:

In [40]: |
x_alpha = nctdtrit(n - 1, |
0, 0.9) |
|||||
|
rb |
= |
1 |
/ (Ex |
- |
(x_alpha * |
sigma2) / math.sqrt(n)) |
|
lb |
= |
1 |
/ (Ex |
+ |
(x_alpha * |
sigma2) / math.sqrt(n)) |
|
[round(lb, 4), |
round(rb, 4)] |
|||||
|
|
|
|
|
|
|
|
Out[40]: |
[1.5031, 2.5214] |
|
|||||
g.e) Используя гистограмму частот, построить критерий значимости
проверки простой гипотезы согласия с показательным распределением с параметром . Проверить гипотезу на
уровне значимости . Вычислить
наибольшее значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Т.к. Гипотеза
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline
$i$ & $I_i$ & $n_i$ & $p_i$ & $np_i$ & $n_i-np_i$ & $\cfrac{(n_i-np_i)^2}{np_i}$ \\
\hline
$1$ & $( - \infty; 1]$ & $41$ & $ 0.5486$ & $ 27.43 $ & $ 13.57 $ & $ 6.7133 $ \\ \hline
$2$ & $(1; +\infty]$ & $9$ & $ 0.4514 & $ 22.57$ & $ -13.57 $ & $ 8.1588 $ \\ \hline
$\sum $ & $ $ & $50$ & $ 1$ & $ $ & $ $ & $ 14.8721 $ \\ \hline
\end{tabular}
In [45]: |
I = |
[[-math.inf, 1], [1, +math.inf]] |
|
|
n_i |
= [41, 9] |
|
|
p_i |
= [] |
|
|
np_i = [] |
|
|
|
n_i_np_i |
= [] |
|
|
res |
= [] |
|
|
for |
i in |
I: |
|
|
p_i.append(round(sp.chi2.cdf(i[1], lam12) - sp.chi2.cdf(i[0], lam12), 4)) |
|
|
for |
i in |
p_i: |
|
|
np_i.append(round(i*n, 4)) |
|
|
|
|
|

for i in range(len(n_i)): n_i_np_i.append(round(n_i[i] - np_i[i], 4))
for i in range(len(n_i)):
res.append(round((n_i_np_i[i] ** 2) / np_i[i] , 4))
res, sum(res)
Out[45]: ([6.7133, 8.1588], 14.8721)
Получаем
Проверим гипотезу на уровне значимости |
: |
Тогда для
Следовательно нулевую гипотезу мы отвергаем. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
g.f) Построить критерий значимости
проверки сложной гипотезы согласия с показательным распределением. Проверить гипотезу на уровне значимости . Вычислить наибольшее
значение уровня значимости, на котором еще нет оснований отвергнуть данную гипотезу.
Минимизируем функцию для :
In [47]: def chi_squared(x): res = 0
for i in range(2):
res_p = sp.chi2.cdf(I[i][1], x) - sp.chi2.cdf(I[i][0], x) res += ((n_i[i]-n*res_p)**2)/(n*res_p)
return res
theta_minimized = float(minimize(chi_squared, lam02).x) print(theta_minimized, chi_squared(theta_minimized))
0.5811253554061293 8.532320796074248e-15
Тогда |
при |
Проверим гипотезу на уровне значимости |
:
Тогда для
Следовательно нулевую гипотезу нельзя отвергнуть. Найдём значение уровня значимости, на котором ещё нет оснований отвергнуть данную гипотезу:
