yoXQhMGFeN

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МУРМАНСКИЙ АРКТИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЬ В НАУКУ

Материалы

межрегиональной научно-практической конференции

13–29 апреля 2016 года

МУРМАНСК

2017

УДК 51+004(082)

ББК 74с51 П90

Печатается по решению Совета по научно-исследовательской работе и редакционно-издательской деятельности Мурманского арктического государственного университета

Рекомендовано к печати кафедрой математики, физики и информационных технологий МАГУ (протокол № 3 от 23 ноября 2016 г.)

Редколлегия: А. А. Ляш, к.п.н., ст. преподаватель кафедры математики, физики и информационных технологий МАГУ (отв. ред.); О.И. Ляш, к.п.н., доцент кафедры математики, физики и информационных технологий МАГУ

Коллектив авторов

П90 Путь в науку : материалы межрегиональной научно-практической конференции, 13–29 апреля 2016 года / отв. ред. А.А. Ляш. – Мурманск : МАГУ,

2017. – 77 с.

Представленный сборник статей включает материалы докладов межрегиональной научно-практической конференции «Путь в науку: первые шаги» (13– 29 апреля 2016 г.) преподавателей и студентов факультета математики, экономики и информационных технологий Мурманского арктического государственного университета и других вузов.

Сборник предназначен для студентов, магистрантов и аспирантов кафедры математики, физики и информационных технологий, а также преподавателей вузов и учителей школ.

Печатается в авторской редакции.

ПРЕДИСЛОВИЕ

Основной целью научно-практической конференции являлась активизация научно-исследовательской деятельности студентов старших курсов, проведение процедуры предварительной защиты выпускных квалификационных работ студентов выпускных курсов, ознакомление студентов с областями научных интересов преподавателей факультета. Также в работе конференции принимали участие студенты младших курсов (1–2 курсы), которые имели возможность попробовать себя в научно-исследовательской работе.

Вработе конференции были затронуты такие направления, как: «Современные технологии разработки программного обеспечения»; «Теория и методика обучения математике»; «Математический анализ»; «Информационные технологии в обучении информатике и ИКТ на различных ступенях обучения»; «Актуальные проблемы управления развитием территорий и качеством жизни в Мурманской области» и некоторые другие.

Впредлагаемый вашему вниманию сборник статей вошли материалы лучших докладов научно-практической конференции «Путь в науку: первые шаги», проходившей на факультете математики, экономики и информационных технологий Мурманского арктического гуманитарного университета в период с 13 по 29 апреля 2016 г., а также статьи преподавателей других вузов, участвовавших в работе конференции заочно.

3

УДК 510.5 ББК 22.18

В.Я. Беляев

ФГБОУ ВО «Мурманский арктический государственный университет» г. Мурманск, Россия

КОМПЬЮТЕРНЫЕ ИССЛЕДОВАНИЯ ПОНЯТИЯ ГЕНЕРИЧНОСТИ

Аннотация. В статье ставится задача исследования генерических множеств с помощью компьютерных экспериментов. Этот способ используется для исследования проблемы остановки машин Тьюринга, работающих на двухсторонней ленте. Приводятся некоторые результаты таких исследований для проблемы остановки машин Тьюринга, работающих на двухсторонней ленте.

Ключевые слова: генерический, полиномиальный алгоритм, машина Тьюринга.

Vladimir Belyaev

Murmansk Arctic State University Murmansk, Russia

COMPUTER RESEARCH OF THE CONCEPT OF GENERICNODE

Abstract. In this paper set the task to study generic sets with help computational experiments. This method is used to study the halting problem of Turing machines working on the double-sided tape.

Key words: generic, polynomial algorithm, the Turing machine.

Понятие генерических множеств и сопутствующее ему понятие асимптотической плотности относятся к теории сложности алгоритмических вычислений. Подробные определения этих понятий имеются в работе [1]. Если не вдаваться в детали, то генеричность некоторого множества R, которое является подмножеством класса конструктивных объектов I, означает, что в R лежат «почти все» элементы I. Ниже приводится точное определение для интересующих нас частных случаев. Пока что заметим, что генерические множества – это множества с асимптотической плотностью, равной 1, а асимптотическая плотность R – это предел отношения (если он существует) |In R|/|In| при n , где In – множество элементов из I, имеющих «размер» n, |A| – мощность множества A (т.е. число его элементов). Под размером конструктивного объекта подразумевается какая-то числовая мера, характеризующая число символов, нужное для записи этого объекта. Множества In всегда предполагаются конечными.

С явлением генеричности в дискретной математике мы сталкиваемся довольно часто. При этом исследований со строгими доказательствами соответствующих фактов до сих пор довольно мало. Многие вопросы, не

4

смотря на кажущуюся простоту, упорно не поддаются аналитическому решению. Вот примеры феномена генеричности, которые ничем не обоснованы кроме опыта.

множество задач линейного программирования, которые за полиномиальное время решаются с помощью симплекс-метода, составляют почти все задачи линейного программирования;

множество начальных конфигураций в известной игре Конуэя «Жизнь», которые быстро «вырождаются» в тривиальные – это почти все конфигурации;

множество КНФ с дизъюнктами из трех литер почти все выполнимы;

почти все конечно определенные полугруппы имеют «простой» алгоритм решения проблема равенства слов.

Настоящая работа посвящена исследованию машин Тьюринга, для которых «полиномиально решается» проблема остановки, когда они стартуют с пустой ленты, бесконечной в обе стороны. Машины Тьюринга, как самая распространенная формализация понятия алгоритма в различных его модификациях, представляют особый интерес. В работе [2] доказано существование генерических множеств машин Тьюринга, которые распознаются за полиномиальное время, но только для случая, когда эти машины работают на односторонней ленте. Для двухсторонних лент вопрос до сих пор открыт.

Метод, с помощью которого проводится данное исследование – многократная случайная генерация машины Тьюринга и наблюдение за ее поведением. Разумеется, и генерация и «наблюдение» осуществляются с помощью специально написанных для этих целей компьютерных программ. Основная цель – экспериментальное обоснование следующего предложения.

Основная Гипотеза. Существует такое множество машин Тьюринга R, что:

1)Принадлежность к R определяется некоторым полиномиальным алгоритмом.

2)Существует полиномиальный алгоритм, решающий для машин из множества R проблему остановки (переходит или нет машина на некотором шаге в заключительное состояние, стартуя с пустой ленты).

3)Множество R является генерическим.

Приведем формальные определения.

Пусть для натурального n 1 Qn = {q1,…,qn} – множество из n символов, элементы которого называются состояниями машины Тьюринга. Дополнительно символ q0 называется конечным состоянием. Машина Тьюринга (МТ) – это функция вида

M : Qn {0,1} (Qn { q0}) {0,1} {L,R}.

5

В традиционном смысле тот факт, что M(qi,s) = (qj,t,H) означает наличие в M команды qis tHqj. Т.к. функция M определена при любых (qi,s) Qn {0,1} и работа машины происходит на ленте, бесконечной в обе стороны, то рассматриваемые МТ никогда не ломаются и единственной причиной прекращения работы для такой машины является ее переход в конечное состояние q0 (остановка). Отметим еще, что на каждом шаге каретка машины сдвигается или на соседнюю клетку влево (Н=L) или на соседнюю клетку вправо (Н=R) и никогда не остается на месте. Наконец, в рассматриваемой формализации внешний алфавит машины состоит только из двух символов 0 и 1. Нас интересует поведение машины после старта с пустой ленты. Под пустой лентой подразумевается лента, все клетки которой заполнены нулями.

Число n будем считать размером машины c областью определения Qn {0,1} и обозначать как n = s(M). Пусть In – множество всех этих машин размера n. Ясно, что это множество конечно и содержит (4(n+1))2n элементов. Пусть I = – множество всех МТ. Для подтверждения основной гипотезы надо подобрать соответствующее множество машин R I. Определим его как

R = ,

где Rn – те машины из In , которые, стартуя с пустой ленты, за не более чем f(n) шагов либо останавливаются, либо зацикливаются, либо циклически уходят влево, либо циклически уходят вправо.

Здесь f(n) – некоторый многочлен от n, который в ходе эксперимента меняется в небольшом диапазоне. Термин «зацикливается» означает, что машина через не более чем f(n) шагов начинает повторять одну и ту же конфигурацию с одной и той же клеткой, в которой находится каретка машины. Термин «машина M циклически уходит влево» (аналогично – вправо) означает, что через не более чем f(n) шагов последовательно встречаются конфигурации (см. рис. 1).

Рис. 1. Зацикливание влево

На рисунке 1 показано:

1) Машина M, стартуя с пустой ленты в начальном состоянии q1 (лента t1), оказывается на некоторой клетке в некотором состоянии qi (лента

6

t2). Справа от этой клетки на ленте появляются слова U(0,1), V(0,1). Это содержимое клеток, на которых побывала каретка машины – на фрагменте вычисления от t1 до t2 она не выходит за границы этих слов.

2)На фрагменте от t2 до t3 машина снова оказывается в состоянии qi строго левее положения каретки на t2. Справа от каретки опять оказывается слово U(0,1). Каретка машины M не заходит на клетки левее или правее слова U(0,1)W(0,1), в которое превращается часть 0..0U(0,1) ленты t2.

3)Преобразование t1 в t3 происходит не более чем за f(n) шагов. Очевидно, что при выполнении этих условий начиная с конфигура-

ции на ленте t2 последовательно будут получаться

qiUV, qiUWV, qiUWWV, qiUWWWV,…

что мы и называем зацикливанием влево.

Легко также видеть, что для конкретного многочлена f(n) имеется полиномиальный алгоритм, диагностирующий по любой машине M, зацикливается M влево или нет. Алгоритм состоит просто в том, что запустив M на пустой ленте, надо сделать f(n) шагов и проследить, встречаются ли конфигурации вида t2 и t3 с условиями 1) и 2). Пусть CLf – множество всех машин Тьюринга M, которые зацикливаются влево за не более чем f(s(M)) шагов.

Аналогично, пусть CRf – множество всех машин Тьюринга M, которые зацикливаются вправо за не более, чем f(s(M)) шагов; CSf – множество всех машин Тьюринга M, которые просто зацикливаются за не более чем f(s(M)) шагов; Sf – множество всех машин Тьюринга M, которые останавливаются за не более, чем f(s(M)) шагов.

Для подтверждения основной гипотезы в качестве множества R возьмем

R = CLf CRf CSf Sf.

Условия 1) и 2) в основной гипотезе очевидны. Например, полиномиальная разрешимость проблемы остановки для M R означает всего лишь проверку, верно или нет, что M Sf.

Для проверки зацикливаемости, допустим, влево, следует проделать f(n) шагов и проверить, не возникает ли где-то ситуация, изображенная на рис. 1. Компьютерная программа в целях большей эффективности работает несколько по-иному. На рис. 1 в конфигурациях t2 и t3 каретка машины находится на первой клетке слова U. На самом деле это не обязательно. Достаточно, чтобы она находилась на какой-то позиции этого слова – одной и той же и для t2 и для t3 и в одном и том же состоянии qi. Тогда произойдет описанное выше зацикливание. Более точно, справедлива

Лемма. Для того, чтобы машина M зацикливалась влево, необходимо и достаточно, чтобы в процессе ее работы встретились конфигурации

(рис. 2):

7

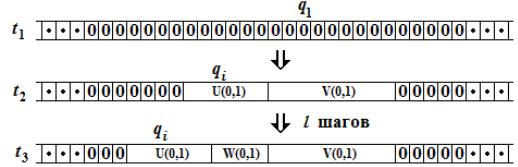
Рис. 2. Зацикливание влево в общем случае

где на лентах t2 и t3 каретка машины находится на одной и той же позиции слова U. Слова U, V, W – это содержимое клеток, на которых каретка МТ была хоть один раз. Слова U и W не пустые. На участке от t2 до t3 каретка МТ не заходит на слово V.

Для доказательства леммы надо просто вместо конфигурации t2 взять конфигурацию после t2, когда каретка первый раз после t2 оказывается на клетке, с которой начинается слово U.

Кроме зацикливания влево при возникновении ситуации на рис. 2, очевидно также, что возникнув один раз эта ситуация дальше будет иметь место на каждом шаге, причем число l (см. рис. 2), которое мы назовем длиной цикла, все время будет одним и тем же.

В силу сказанного достаточно эффективная проверка зацикливания влево (для зацикливания или зацикливания вправо – аналогично) состоит в следующем. Сначала МТ делает сколько-то шагов без всяких проверок. На каждом шаге пересчитываются координаты kmin и kmax клеток, очерчивающих границы использованной части ленты. Затем начинаются проверки зацикливания. Причем не тотальные, а выборочные и с некоторых шагов.

Каждая проверка – это те же стандартные шаги МТ, но в особом режиме. При переходе в этот режим во временной памяти сохраняется содержимое ленты (это t2 на рис. 2), текущая клетка (допустим, k), текущее

состояние (допустим, qi), kmin(t2) =kmin и kmax(t2)=kmax. Далее, дополнительно к kmin и kmax на каждом шаге вычисляется расширяющийся от [k,k] проме-

жуток [k1,k2] с номерами позиций, на которых побывала каретка машины после t2. И как только МТ вновь оказывается в состоянии qi, делается проверка полученной конфигурации на предмет зацикливания или зацикливания влево или зацикливания вправо. Например, для проверки зацикливания влево надо, чтобы позиция r каретки, когда машина перешла в qi, оказалась

строго меньше k. Информации о значениях kmin(t2), kmax(t2), k1, k2, kmin и kmax теперь достаточно для проверки годится ли полученная конфигурация в

качестве t3 на рис. 2. Надо всего лишь, чтобы часть t2 от kmin(t2) до k2 совпала с частью t3 от kmin до kmin + ( k2 – kmin(t2) + 1) и чтобы k – kmin(t2)= r – kmin.

8

Основной вопрос – условие 3) – является ли множество R генерическим, пока открыт. Демонстрируемые далее результаты компьютерных экспериментов показывают, что при подходящем выборе f(n) это очень похоже на правду.

Генеричность R означает, что = 1. Мы хотим подтвердить это соотношение с помощью компьютерных вычислений. Сразу понятно,

что даже при сравнительно небольших n вычисление отношения не

возможно ни на каком суперкомпьютере. Однако мы получим неплохое приближение этого отношения, если будем рассматривать не все подряд МТ из In, а только случайные выборки машин из этого множества. Для того, чтобы у всех машин была одинаковая вероятность попасть в выборку, мы применяем следующий простой алгоритм генерации МТ. Машина M представляет собой вектор-функцию из трех компонент (q, t, H), каждая из которых есть заполнение таблицы

0

1

Для функции q в каждой клетке помещается одно из состояний

q0 , q1 , q2 ,…, qn – каждое с вероятностью 1/(n+1).

Для функции t в каждой клетке помещается один из символов 0,1 – каждый с вероятностью 0.5.

Для функции H в каждой клетке помещается один из символов R, L – каждый с вероятностью 0.5.

Итак, программа, проверяющая основную гипотезу работает следующим образом.

a)Входом являются настройки со следующей информацией:

промежуток для значений n – допустим от n1 до n2;

число экспериментов для каждого n – допустим m;

в качестве многочлена f(n) выбирались некоторые линейные f(n)= n/2, f(n)= n , второй степени f(n)= 10n2 , третьей f(n)= n3.

b)Для каждого n от n1 до n2 случайным образом, как описано выше, создается машина Тьюринга M.

c)Вычисляется последовательность конфигураций при старте M с пустой ленты для f(n) шагов работы МТ.

d)Если машина не останавливалась, то делается проверка зацикливания какого-либо типа. Из леммы следует, что зацикливание можно проверять с любого места. Например, после вычисления всех f(n) шагов. Но как показали численные эксперименты, чаще всего цикл выявляется гораз-

9