
Лекция2
.pdf
Лекция 2.
Существующие методы компактной диагностики цифровых схем (ЦС).
Общая классификация методов компактного тестирования может быть представлена
в виде следующей блок-схемы (рис.1):
Рис1. Методы компактной диагностики
Рассмотрим каждый из методов подробнее:
Детерминированные методы.
1. Метод счета переходов.
Широко распространенный и простой способ контроля заключается в том, чтобы подсчитать переходы сигнала из одного состояния в другое и использовать полученное число в качестве идентификатора узла. Общее число изменений состояния тестируемого узла может быть очень большим, поэтому необходим какой-то способ сжатия информации. Обязательным условием счета переходов является определенное "временное окно", в течение которого подсчитываются переходы в узле. В интервале "временного окна" выполняется тест-программа, которая проверяет узел и по возможности должна быть периодической для удобства воспроизведения и сравнения результатов нескольких измерений. В конкретной системе результаты нескольких подсчетов переходов должны быть идентичными.
Для применения метода счета переходов (СП) как способа поиска неисправностей необходимо измерить и записать эталонные числа переходов в каждом узле. При возникновении неисправности исследователь запускает тест-программу, измеряет число переходов в подозреваемых узлах и сравнивает их с эталонными значениями. Любые расхождения свидетельствуют о наличии неисправности, и с помощью систематической процедуры ее можно локализовать.
2. Синдромный метод
Основные положения синдромного тестирования во многом похожи на положения, рассмотренного ранее, метода счета переходов.
Синдромом (контрольной суммой) некоторой булевой функции n переменных является соотношение:
SR2
2n
где R2 представляет собой количество единиц во входной последовательности {y(k)},
l=2n.
l
R2 y(k) , l=2n.
k 1
Определение понятия синдрома однозначно предполагает использование генераторов счетчиковых последовательностей для формирования всевозможных двоичных комбинаций из n входных переменных при тестировании схемы, реализующей заданную функцию.
На практике наиболее важна взаимосвязь синдрома, полученного для выходной последовательности элемента, со значениями синдромов его входных последовательностей, что позволит аналитически определить значения синдромов на всех полюсах схемы.
Вероятностный метод.
Отличительная особенность данного вида тестирования состоит в применении последовательностей случайных независимых двоичных цифр, подаваемых на входы прове-
ряемой цифровой схемы (ЦС). При этом переменная xi 0,1 i=1, n , подаваемая на i-тый вход, описывается вероятностью P(xi=1) ее единичного значения. Определяется зависимость выходных вероятностей для цифровой схемы от вероятностей P(xi=1) i=1, n . Клас-
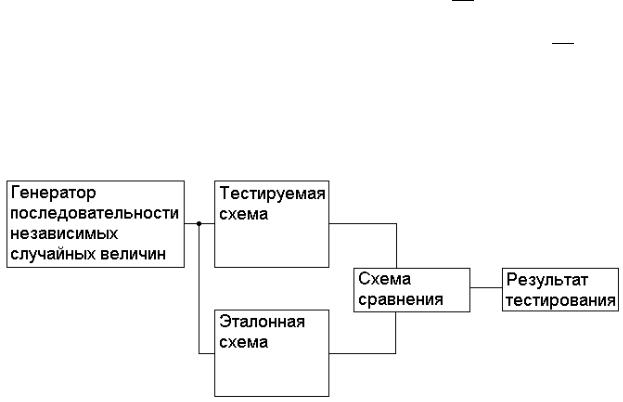
сическая схема вероятностного тестирования представлена на рис.1. Такие вероятности называются сигнальными. С их помощью можно определить вероятность появления единичного сигнала на заданных полюсах.
Рис. 1. Классическая схема вероятностного тестирования
3. Сигнатурный анализ.
4. Замкнутые системы диагностики.
Особенности замкнутых систем обусловлены эффектом "размножения" дефекта по контуру, усиливающим обнаруживающие способности.
Замкнутость компактных систем тестирования в значительной мере способствует разрешению противоречия, обусловленного отставанием характеристик старых средств тестирования от характеристик вновь создаваемого объекта. Поскольку в процессе функционирования встроенных средств таких систем отсутствуют обращения к запоминающим устройствам и сравнения фактических ответов с эталонными, то возможно проведение проверок на высокой рабочей частоте объекта .
С развитием замкнутых систем тестирования связано появление системы кольцевого тестирования. В кольцевых системах функции генератора и анализатора совмещаются в пространстве и во времени, топология структуры имеет форму кольца, модели систем описываются в алгебре кольца многочленов и кольцевыми (циклическими) графами, что породило термин кольцевое тестирование (в дальнейшем КТ). В процессе проверки исправная система проходит свои состояния по циклическому маршруту. Поэтому заключение об исправности объекта делается на основании сравнения начального и конечного состояний системы.
Для компактной диагностики многовыходных цифровых схем особый интерес представляют два метода: сигнатурный анализатор (разомкнутая система) и кольцевое тестирование (замкнутая система).
Принципы генерирования случайных и псевдослучайных последовательностей.
Взадачах активных экспериментальных исследований современных сложных технических систем с применением статистических методов важное место принадлежит генерированию сигналов возбуждения. Диктуется это не только необходимостью подачи на объект требуемого числа воздействий с заданными свойствами, но и максимальной скорости их выработки. Одним из наиболее распространенных в настоящее время методов формирования таких процессов является преобразование сигналов, получаемых с помощью так называемых генераторов белого шума (ГБШ). В применении к цифровым методам генерирования под белым шумом понимается последовательность некоррелированных чисел или цифр, распределенных, как правило, по равномерному закону.
Известны два основных метода получения цифрового белого шума: физический — генерирование случайных двоичных чисел с помощью специальных устройств — генераторов случайных чисел (ГСЧ); математический— формирование псевдослучайных числовых последовательностей (ПСЧП) по специальным программам или с использованием генераторов псевдослучайных чисел (ГПСЧ).
Возможен также и третий путь, совмещающий в себе физический и математический принципы.
Принцип действия ГСЧ состоит в преобразовании случайного сигнала на выходе физического источника шума в импульсную последовательность с вероятностью появления импульса р (1) = 0,5.
Взависимости от способа формирования числовых последовательностей ,существующие ГСЧ можно разделить на четыре основных типа:
1) ГСЧ, основанные на использовании случайных состояний бистабильной схемы при периодическом включении и выключении источника питания;
2) ГСЧ с пересчетом импульсов периодической последовательности за случайный интервал времени;
3) ГСЧ с пересчетом импульсов случайной последовательности за фиксированный интервал времени;
4) ГСЧ, основанные на дискретизации непрерывного шумового сигнала по двум уровням.
Наиболее часто при разработке быстродействующих и высококачественных ГСЧ применяются последних два способа.
В генераторах с пересчетом случайных импульсов за фиксированный интервал времени равновероятность символов выходной последовательности достигается путем выполнения суммирования по модулю два. В то же время данная операция, протекающая последовательно во времени, снижает быстродействие ГСЧ, что ограничивает область их применения. Более высоким быстродействием обладают ГСЧ, основанные на дискретизации непрерывного шумового сигнала по двум уровням. Однако данным устройствам свойственна высокая чувствительность к изменениям параметров первичного шумового сигнала, главным образом его среднего значения.
Общими и наиболее существенными недостатками, затрудняющими применение ГБШ, являются следующие факторы:
1.ограниченное быстродействие, определяемое первичным аналоговым источником
шума;
2.низкая стабильность основных вероятностных характеристик, объясняемая нестабильностью первичных источников, дрейфом параметров преобразующих схем, источников питания и др., что требует периодической статистической проверки качества генерируемой последовательности;
3.сложность аппаратурной реализации, вызываемая наличием нескольких источников питания (для физического источника шума и цифровых схем), необходимостью стабилизации и фильтрации их напряжения, развязки линий питания от линий устройства, коррекции выходной последовательности и др.;
4.невозможность воспроизведения и предсказания генерируемых последовательностей в силу их случайной природы; неоднородность структуры генераторов вследствие наличия как аналоговых, так и цифровых узлов, что затрудняет миниатюризацию ГСЧ.
Указанные недостатки физических ГСЧ явились причиной все более широкого распространения математических методов получения шумовых числовых последовательностей. Мгновенные значения таких псевдослучайных последовательностей в отличие от случайных последовательностей в принципе, могут быть предсказаны заранее. В то же время все оценки статистических характеристик конкретной реализации ПСЧП совпадают
соценками соответствующей ей случайной выборки. Любую статистическую характеристику псевдослучайной числовой последовательности можно получить, используя реализацию длиной в один период повторения ПСЧП. Для истинно случайной последовательности это потребовало бы бесконечно большую длину реализации. Искусственное увеличение периода ПС-сигнала неограниченно приближает его структуру к структуре одной из возможных реализаций истинно случайного процесса. Однако и при ограниченных величинах периода в определенных условиях псевдослучайные числовые последовательности могут заменить случайные. При анализе псевдослучайной реализации равной или меньшей длине периода вообще практически невозможно определить, является ли она отрезком регулярной или случайной последовательности. С другой стороны, если записать конкретную случайную реализацию на каком-либо носителе, и периодически воспроизводить ее, то получим регулярную ПСЧП.
Таким образом, с точки зрения реальных характеристик трудно установить границу между случайными и псевдослучайными числовыми последовательностями. В то же время применение ПСЧП имеет ряд существенных преимуществ:
1. периодический характер псевдослучайного сигнала обусловливает низкий уровень дисперсии оценок, получаемых при усреднении в течение целого числа периодов; характеристики ПСЧП абсолютно стабильны и определяются алгоритмом формирования псевдослучайных чисел;
2. последовательность можно повторить с любого желаемого участка реализации, для чего не требуется сложных запоминающих устройств и др.
Наиболее часто при генерировании ПСПЧ с равномерным распределением используются два метода. Первый, лежащий в основе большинства современных программных датчиков и некоторых специализированных устройств, описывается рекуррентным соотношением:
Xk=AXk-1+C(mod R), k=1,2,3,…
где A,C,R - постоянные числа; X0>0, A>0, C>0, R>X0, R> A, R>C.
Данный метод получил название мультипликативного конгруэнтного (при с=0) или смешанного конгруэнтного (при с>0), а формируемая в соответствии последовательность – линейной конгруэнтной.
Второй метод наиболее часто используется в аппаратурных псевдослучайных датчиках и узлах ЭВМ и заключается в получении линейной двоичной последовательности по рекуррентному выражению:
ak |
|
m |
|
i ak i |
|
|
|
|
k = 0, 1, 2, 3, . . . , |
(2.1) |
|||
|
|
i 1 |
|
ai {0,1}—символы |
|
|
где |
k |
— |
номер такта; |
выходной последовательности; |
||
|
|
|
|
|
|
|
i 0,1 — постоянные коэффициенты; знак |
означает суммирование по модулю |
|||||
два.
При соответствующем выборе коэффициентов k генерируемая числовая после-
довательность (ЧП) имеет максимальную величину периода и называется M- последовательностью.
Оценка эффективности представленных методов математического генерирования предусматривает исследование свойств формируемых ПСЧП.
Построение генераторов с линейными обратными связями.
Одним из главных преимуществ метода генерирования ПС–последовательностей максимальной длины является простота его реализации. Важнейшим классом ПСП являются последовательности, формируемые генераторами на основе регистров сдвига с ли-
нейными обратными связями –LFSR (Linear Feedback Shift Register) .
Используемый при анализе генераторов с линейными обратными связями математический аппарат – теория линейных последовательностных машин и теория конечных полей. Основными достоинствами этих генераторов являются
-простота аппаратурной реализации;
-максимальное быстродействие;
-хорошие статистические свойства формируемых последовательностей;
-возможность на их основе построение генераторов, обладающих свойствами, ценными при решении специфических задач защиты информации (формирование последовательностей произвольной длины, формирование последовательностей с предпериодом , формирование ПСП с произвольным законом распределения ,построение генераторов, обладающих свойством самоконтроля и т.п.)
Генератор с линейными обратными связями представляет собой устройство, состоящее из двоичных запоминающих элементов, образующих регистр сдвига, и набора сумматоров по модулю два, служащих для формирования очередного значения последовательности. При этом сумматоры могут быть включены как во внешние цепи ОС генератора, так и в межразрядные связи элементов памяти регистра сдвига
Аппаратурный генератор ПСП, функционирующий в соответствии с выражением (2.1), содержит m—разрядный регистр сдвига (РС) и набор сумматоров по модулю два,

включенные во внешние цепи обратной связи (ОС) (рис.2.1). В процессе функционирования генератора РС выполняет хранение и сдвиг вправо предшествующих символов последовательности, а сумматоры в цепи обратной связи производят вычисление значений очередных символов, которые последовательно записываются в самый левый разряд регистра
.
рис.2.1.
Если последовательность состояний РС представить как последовательность m— мерных векторов А = (a1,a2,…am), где αn€{0,1}, n=1,m то преобразование, осуществляемое схемой в некотором к – м такте работы, можно записать в матричной форме:
|
a1 (k 1) |
|
1 |
2 ... |
m 1 |
m |
|
a1 |
(k) |
|
|
|
|
|
|||||||
|
a2 (k 1) |
|
1 |
0 ... |
0 |
0 |
|
a2 |
(k) |
|
|
a3 (k 1) |
|
0 |
1 ... |
0 |
0 |
|
a3 |
(k) |
(2.2) |
|
|
|||||||||
|
... |
|
... ... ... ... |
... |
|
... |
|
|||
|
am (k 1) |
|
0 |
0 ... |
1 |
0 |
|
am (k) |
|
|
или в более компактном виде |
|
|
|
|||
A(k 1) VAk |
|
|
|
(2.2а) |
||
где |
|
|
|
|
|
|
|
1 |
2 ... |
m 1 |
m |
|
|
|
|
|||||
|
1 |
0 ... |
0 |
0 |
|
|
V |
0 |
1 ... |
0 |
0 |
|
|
|
... ... ... ... |
... |
|
|
||
|
0 |
0 ... |
1 |
0 |
|
(2.2б) |
|
|
|
|
|
|
|
|
|
|
|
|
||
Последовательное применение (2.1) позволяет найти состояние РС генератора в про- |
||||||
извольный последующий такт работы: |
||||||
A(k s) |
V s Ak |
|
|
|
(2.2в) |
|
Аппаратурный генератор ПСП, в котором ОС включены в межразрядные связи элементов памяти регистра сдвига, представлен на рис.2.2.
Рис.2.2
Для построения таких генераторов выражение 2.2, матрица V записывается как (2.3),
а коэффициенты α определяются из обратного полинома 1(x) xm (x 1 ) .
0 |
0 |
0 ... |
0 |
1 |
|
|
||
|
1 |
0 |
0 ... |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
1 |
0 ... |
0 |
2 |
|
(2.3) |
|
VM |
0 |
0 |
1 ... |
0 |
|
|
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|||
... ... ... ... ... |
... |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 ... |
1 |
m 1 |
|
||
Генераторы М-последовательности.
Циклические свойства генератора ПС последовательности определяются характеристическим многочленом:
|
m |
|
(x) |
i xi , где α0=αm=1 . |
(2.4) |
|
i 0 |
|
При соответствующем выборе коэффициентов αi на основании характеристического полинома (2.4). который должен быть неприводимым и примитивным, последовательность
имеет максимальную длину, равную L 2m 1 . Такая последовательность называется M-последовательностью. Неприводимым называется такой многочлен φ(x) степени m, который не делится ни на какой другой многочлен от пониженной степени. Примитивным
характеристический полином φ(x) будет в том случае, если полином X L 1 делится на
полином φ(x) только при L 2m 1. При этом необходимо, чтобы начальное состояние регистра сдвига не было нулевым, так как в противном случае генерируемая последовательность будет состоять из одних нулей, что соответствует тривиальному нулевому циклу генератору.
Основная задача синтеза генератора ПС—последовательности максимальной длины это нахождение многочлена φ(x), удовлетворяющего условию примитивности и неприводимости. Известно, что для данного m существует Ф(L)/m примитивных различных и неприводимых полиномов, где Ф(L)—функция Эйлера. Поскольку с ростом m число Ф(L) быстро увеличивается, то соответственно возрастает и количество многочленов φ(x) степени m, порождающих М—последовательности. Среди этого множества можно отыскать полиномы, имеющие наименьшее число нулевых членов. Данный случай характерен для минимальной конфигурации ГПСЧ, где в состав цепи ОС входит наименьшее число сумматоров по модулю два.
Необходимо отметить, что для формирования М–последовательности наряду с примитивным неприводимым полиномом φ(x) может использоваться и обратный ему
1(x) xm (x 1 ) . Получаемая в этом случае последовательность максимальной длины будет инверсна по отношению к последовательности, порождаемой φ(х).
Так как нулевое состояние регистра ГПК является запрещенным, максимально возможное число состояний устройства, а значит, и максимально возможная длина формируемой двоичной последовательности, снимаемой с выхода любого из триггеров, равны 2m-1. В этом случае диаграмма состояний генератора состоит из одного тривиального цикла и цикла максимальной длины 2m – 1.
В качестве примера на рис. 2.2.2 показаны альтернативные структуры генераторов M- последовательностей для порождающего полинома M(x)=x4 x3 1, а в табл. 2.2.1 представлена последовательность смены состояний их регистров сдвига при AM(0) = A(0)=1000. В соответствии с (2.2.2) для рассматриваемого примера имеем
a1 |
(k 1) |
|
0 |
|
|
|
|
a2 |
(k 1) |
|
1 |
a3 |
(k 1) |
0 |
|
|
|
|
|
a4 |
(k 1) |
|
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
0 |
1 |
0 |
|
a1 |
(k) |
|
|
a |
|
(k) |
|
|
2 |
. |
(2.5) |
a3 |
(k) |
|
|
|
|
|
|
a4 |
(k) |
|
|
Для построения одноканального генератора М-последовательности получим систему логических уравнений:
a1(k 1) a3 (k ) a4 (k )
a2 (k 1) a1(k )
(2.6)
a3 (k 1) a2 (k )
a4 (k 1) a3 (k )
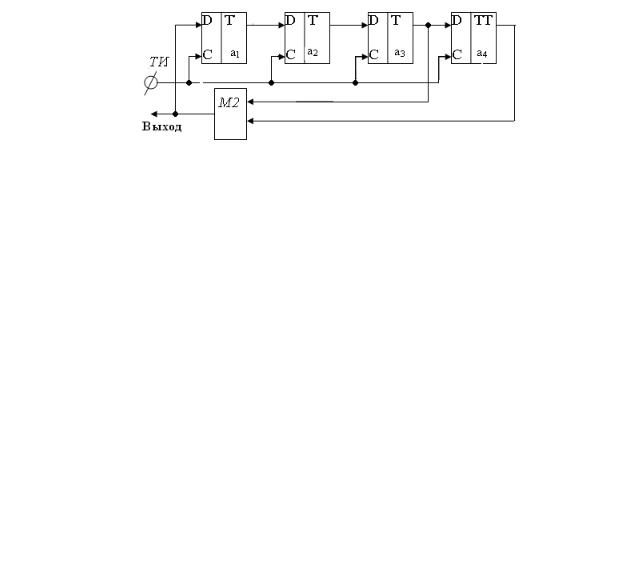
На рис. 2.3 изображена схема генератора М-последовательности для полинома в соответствии с системой логических уравнений (2.6),а в табл. 2.1 представлена последовательность смены состояний регистров сдвига при начальном состоянии A(0)=1000. Регистр сдвига реализован на D-триггерах, состояния которых изменяются по приходу на С- входы тактовых импульсов .
Рис.2.3
Таблица 2.1
№ такта |
а1 |
а2 |
а3 |
а4 |
Выход |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
1 |
3 |
1 |
0 |
0 |
1 |
1 |
4 |
1 |
1 |
0 |
0 |
0 |
5 |
0 |
1 |
1 |
0 |
1 |
6 |
1 |
0 |
1 |
1 |
0 |
7 |
0 |
1 |
0 |
1 |
1 |
8 |
1 |
0 |
1 |
0 |
1 |
9 |
1 |
1 |
0 |
1 |
1 |
10 |
1 |
1 |
1 |
0 |
0 |
11 |
1 |
1 |
1 |
1 |
0 |
12 |
0 |
1 |
1 |
1 |
0 |
13 |
0 |
0 |
1 |
1 |
1 |
14 |
0 |
0 |
0 |
1 |
1 |
15 |
1 |
0 |
0 |
0 |
0 |
Из табл.2.1 следует, что длина формируемой последовательности равна 15, т.е. через 15 тактов регистр устанавливается в начальное состояние.
Перейдём к рассмотрению свойств последовательностей максимальной длины . 1. Период М–последовательности, формируемый в соответствии с выражением
ak |
m |
|
i ak i , k = 0, 1, 2, 3, . . . , |
|
|
||
|
i 1 |
|
|
где аk€{0,1}–символы последовательности; αi€{0,1}–коэффициенты, определяемые примитивным неприводимым порождающим полиномом φ(х), для которого m=deg φ(х), равен 2m - 1.
2.Для заданного φ(х) существует L различных М—последовательностей, сдвинутых относительно друг друга.
3.Число единичных символов на периоде М—последовательности равно 2m-1, а нуле- вых—2m-1-1. Вероятности появления 1 и 0 определяются выражениями
p(a 1) |
2m 1 |
|
|
1 |
|
1 |
|
|
p(a 0) |
2m 1 |
1 |
|
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
2m 1 |
|
|||||||
2m 1 |
2 |
2m 1 |
2 ; |
2m 1 |
2 |
2 |
||||||||||||
i |
|
|
i |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и при увеличении m достигают значений сколь угодно близких к 0,5.
4. В псевдослучайной последовательности максимальной длины серии из одного символа (1 или 0) встречаются 2m-2 раз, из двух единиц или нулей 2m-3 и т.д. Серии из m-1 нулей и m единиц встречаются лишь по одному разу. Сравнивая выражения для оценки вероятности появлении серий из l одинаковых символов, можно убедиться в их практической эквивалентности.
5. Для каждого целого s(l≤s<L) существует такое целое r≠s (l≤r<L), что {ai} {ai-s}={ai-r}. Данное свойство обычно называют свойством сдвига и сложения.
6. Автокорреляционная функция М–последовательности определяется выражением
1 при 0(mod L),
Ra ( ) 1/ L при 0(mod L).
7. Децимацией последовательности {ai} по индексу q(q=1, 2, 3,…) называется формирование новой последовательности {bi} из q—х элементов {ai}, т.е. bk=akq. Если {bi} является нулевой последовательностью, то она порождается полиномом ψ(х), и имеет период L/(L,q), где (L,q)наибольший общий делитель L и q. При (L,q)=1период {bi} равен L=2m-1, где m=deg φ(х), и децимация называется собственной или нормальной.
Результатом всякой нормальной децимации является М–последовательность периода L, порождаемая примитивным неприводимым полиномом ψ(х). При этом если децимация выполняется над последовательностью, сдвинутой на j тактов относительно исходной {ai}, то получаемая последовательность будет также сдвинутой на некоторое число j тактов по сравнению с {bi}. Иначе говоря, независимо от того, какой именно сдвиг последовательности, порождаемой полиномом φ(х), выбран, результатом ее всегда оказывается М– последовательность, порождаемая полиномом ψ(х). В частности, при децимации характеристической М—последовательности {ai}*, порождаемой многочленом φ(х), получается также характеристическая последовательность {bi}*, соответствующая полиному ψ(х).
Рассмотрим несколько разновидностей М—последовательностей, формируемых в результате нормальных децимаций. Поскольку децимация по индексу q будет давать тот же результат, что и децимация по q(mod L), ограничимся q≤L. Прежде всего, очевидно, что децимация по единичному индексу будет равна исходной последовательности bk=ak*l=ak. Результатом децимации характеристической последовательности по индексу 2 будет исходная характеристическая последовательность bk*=a2k*=ak*. Следовательно, для произвольной последовательности {ai} существует такое n, при котором ее децимация {ai} по индексу 2 равна сдвигу на n тактов ak2=ak-n. Отсюда следует, что характеристическая последовательность {ai}* есть результат сдвига исходной {ai} на 2*n тактов, a*k=a*k-2n. Тогда, поскольку для любого s a*2ks=ak, справедливо равенство a2ks=ak-r, где величина сдвига
r зависит от s. В общем случае М—последовательность периода L может быть сформирована из исходной посредством ее децимации по нечетному индексу q.
Среди децимации по четному индексу выделяют случай q=L-1, при котором bk=ak(l- 1)=a-k. Иными словами, последовательность {bi} является инверсной к {ai} и порождается
полиномом ψ(х), обратным к φ(х), ψ(х)=φ 1 (х).
Данное свойство это—тест, позволяет различать М—последовательности и последовательности случайных двоичных цифр. Пусть а0,а1,…,аn-1—сегмент М– последовательности периода L=2m-1, где n<L. Составим матрицу:
|
a0 |
a1 ... |
an b |
M |
a1 |
a2 ... |
an b 1 |
... ... ... |
... |
||
|
ab 1 |
ab ... |
an 1 |
где m<b<n/2. ранг данной матрицы меньше величины b, что следует из наличия линейной зависимости между символами М—последовательности. С другой стороны, если а0а1…аn- 1—последовательность равновероятных двоичных случайных цифр, то вероятность того, что rang(M)<b, не превышает 22b-n-1 и при соответствующем выборе b и n оказывается весьма незначительной величиной.
Таким образом, вопрос rang(M)<b? является тестом, с помощью которого по ограниченному числу элементов М—последовательности можно показать, ее отклонение от абсолютной случайности. Например, при m=11, L=2m-1=2047 и b=15 для М— последовательности rang(M)<b, начиная с n=50, тогда, как вероятность получить такой же результат для случайной последовательности не превышает 2-21.
Многоканальные генераторы М-последовательностей.
Если последовательность состояний регистра сдвига представить как последовательность m—мерных векторов А=(a1,a2,… a m), где a n€{0,1}, n=1,m то преобразование, осущес т вляемое схемой в некотором к–ом такте работы, можно записать в матричной форме:
a1 |
(k 1) |
1 |
2 ... |
||||
a |
|
(k 1) |
|
|
1 |
0 ... |
|
|
|
2 |
|
|
|
|
|
a3 |
(k 1) |
|
|
0 |
1 ... |
||
|
|
|
... |
|
|
|
|
|
|
|
|
... ... ... |
|||
a |
m |
(k 1) |
|
0 |
0 ... |
||
|
|
|
|
|
|
||
или в более компактном виде
, A(k 1) VAk
где
m 1 |
m |
a1(k) |
|
||||
|
|
|
|
|
|
|
|
0 |
0 |
|
a2 |
(k) |
|
||
0 |
0 |
* a3 |
(k) |
|
|||
|
|
|
|
|
|
|
(2.5) |
... |
... |
... |
|
|
|||
1 |
0 |
|
a |
m |
(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2. 6) |
