
Лекция2
.pdf1 |
2 ... |
m 1 |
m |
|
||
|
1 |
0 ... |
0 |
0 |
|
|
|
|
|
||||
V |
0 |
1 ... |
0 |
0 |
|
|
|
|
|
|
|
|
|
... ... ... ... |
... |
|
||||
|
0 |
0 ... |
1 |
0 |
|
|
|
|
(2. 7) |
||||
Таким образом, при последовательном применении выраже ния (2.6 ), можно определить состояние регистра сдвига генер атора в произвольный последующий такт работы:
A(k s) V s A(k)
, (2. 8)
где s – это величина сдвига.
Реализация многок анального генератора М -последовательности.
Рассмотрим построение двухканального генератора М - последовательности, т.е. n -S=2. В качестве порождающего полинома выб е- рем (x)=x4 x3 1. В соответствии с (2.8) для рассматриваемого примера имеем
a1 |
(k 1) |
|
0 |
0 |
1 |
1 2 |
|
a1 |
(k) |
|
0110 |
|
a1 |
(k) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
(k 1) |
|
1 |
0 |
0 |
0 |
|
a2 |
(k) |
|
0011 |
|
a2 |
(k) . |
||||||||||
|
a |
3 |
(k 1) |
|
|
|
|
|
|
a |
3 |
(k) |
|
|
|
|
|
3 |
|
|
||||
|
|
|
0 |
1 |
0 |
0 |
|
|
|
1000 |
|
|
a |
|
(k) |
|
||||||||
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a4 |
(k 1) |
|
0 |
0 |
|
a4 |
(k) |
|
0100 |
|
a4 |
(k) |
||||||||||||
Для построения одноканального генератора М-последовательности получим систему логических уравнений:
a1(k 1) a2 (k ) a3 (k )
a2 (k 1) a3 (k ) a4 (k )
(2.9)
a3 (k 1) a1(k ) a4 (k 1) a2 (k ).
На рис. 2.3 изображена схема генератора М-последовательности для полинома в соответст-
вии с системой логических уравнений (2.9).
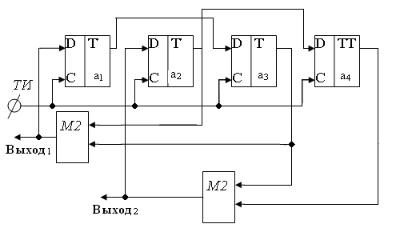
Рис.2.9
Проектирование восьмиразрядного генератора псевдослучайных чисел для порождающе-
го полинома 8-ой степени (x) x8 x6 x5 x 1 и величины сдвига S=8:
|
|
|
1 0 0 0 1 1 |
0 |
1 8 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 0 0 0 0 0 |
0 |
0 |
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 1 0 0 0 0 |
0 |
|
0 |
|
V |
8 |
|
0 0 1 0 0 0 |
0 |
0 |
|
0 |
|
0 0 0 1 0 0 |
0 |
0 |
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
0 0 0 0 1 0 |
0 |
0 |
|
1 |
|
|
|
0 0 0 0 0 1 |
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 0 0 0 0 0 |
1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
a (k 8) |
|
|
1 1 0 1 1 0 |
|
|
1 |
|
|
|
a2 (k 8) |
|
0 1 1 0 1 1 |
||
|
|
|
|
|
a3 (k 8) |
|
0 0 1 1 0 1 |
||
a4 (k 8) |
|
0 0 0 1 1 0 |
||
a (k 8) |
1 1 0 0 1 0 |
|||
|
5 |
|
|
|
a6 (k 8) |
|
1 0 1 0 0 0 |
||
a (k 8) |
|
1 0 0 1 0 1 |
||
|
7 |
|
|
|
a (k 8) |
|
1 0 0 0 1 1 |
||
|
8 |
|
|
|
и система логических уравнений:
0 |
0 |
|
a (k) |
|
|
|
|
|
|
1 |
|
0 |
0 |
|
a2 (k) |
||
1 |
|
|
|
|
|
0 |
|
a3 (k) |
|
||
1 |
1 |
|
a4 (k) |
||
1 |
1 |
a (k) |
|||
|
|
|
|
5 |
|
1 |
1 |
|
a6 (k) |
||
1 |
1 |
|
a (k) |
||
|
|
|
|
7 |
|
0 |
1 |
|
a (k) |
|
|
|
|
|
|
8 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
||||||
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
a1 (k 8) a1 (k) a2 (k) a4 (k) a5 (k) a2 (k 8) a2 (k) a3 (k) a5 (k) a6 (k) a3 (k 8) a3 (k) a4 (k) a6 (k) a7 (k) a4 (k 8) a4 (k) a5 (k) a7 (k) a8 (k)
a5 (k 8) a1 (k) a2 (k) a5 (k) a7 (k) a8 (k) a6 (k 8) a1 (k) a3 (k) a7 (k) a8 (k)
a7 (k 8) a1 (k) a4 (k) a6 (k) a7 (k) a8 (k) a8 (k 8) a1 (k) a5 (k) a6 (k) a8 (k)
Применение генераторов псевдослучайных тестовых последовател ь-
ностей д ля диагностики цифровых схем.
Синтез ГПТП для комбинационных схем.
Любую комбинационную схему G можно представить в виде множес т- ва ф ункционально независимых подсхем Gi, i={1,l} имеющих ri≥1 входов и vi≥1 выходов, где ∑ ri=r—количество входов схемы G, а ∑vi=v —количество ее выходов.
Для поверки правильности ф ункционирования схемы G необходимо на каждую подсхему Gi подать всевозможные входные н аборы
В случае формирования тестовых последовательностей с помощью генер а- тора М —последовательности для обеспечения всев озможных входных наб о- ров на входах схемы G необходимым является выполнение н еравенства:
degφ (x)>r, |
(2.9) |
где degφ (x)=m— старшая степень порождающего полинома φ(x ). При этом
длина тестовой последовательности N 2deg ( x) 1 2r .
Цифровые схемы имеют до 480 входов, поэтому их контроль с и с- пользованием М —последовательностей , для которых degφ (x)>30 -40, являет - ся не реальной задачей .
В случае проверки правильности ф ункциониров ания цифр овой схемы не на полном периоде М —последовательности нельзя гарант ировать 100% — ную полнот у обнаружения всех ее неисправностей. В настоящее время предпринимаются попытки обеспечения 100% —ной полноты покрытия при использовании М — последовательности с длинной периода L 2m 1 за счет формирования всевозможных входных наб оров.
Выражение (2.9 ) дает верхнюю оценк у величины m , определяющей значение старшей степени порождающего полинома φ(х), использование к о - торого на контроле схемы G позволи т достичь максимальной полноты ко н - троля. Нижняя оценка для m=degφ (x ) будет определяться соотнош ением degφ (x)>max ri , однако это выражение только необходимое, но не достато ч- ное условие, которому должен удовлетворять порождающий пол ином φ (x). Достаточным усл овием (на его основе формируется тестовая псевдослуча й - ная последовательность ) является обеспечение линейной незав и симости символов, подаваемых одновременно на входы проверяемой комбинацио н - ной схемы.
Каждому входу проверяемой комбинационной схемы соответств ует определенный разряд входного регистра; таким образом, любой вход i—й
комбинационной схемы можно обозначить как Sc i , где с —порядковый номер входа подсхемы Gi , подключенный к Sc i — разряду входного разряда, где
формируются псевдослучайные тестовые наборы. Для выполнения необх о- димого условия значение с={1, ri} должно быть ограничено величиной m. В
то же время Sc i €{1,2,3,.., p} (p>m —количество разрядов входного регистра). В зависимости от соотношения величин p и m и от значений Sc i воз-
можны два тривиальных случая выполнения достаточных условий, предъя в- ляемых к порождающему полиному φ (x ), когда на выходы каждой подсхемы множества Gi будут поданы всевозможные двоичные наборы. Достато чные условия будут выполняться при:
p=m и, во— вторых, при p>m и
max(max Sc i -min Sc i )<m. Для случая i €{1,l},
max Sc i -min Sc i ≥m необходимо обеспечение линейной
независимости символ ов входных наборов. Это достигается выбором соот ветствующего порождающего полинома φ (x ) из множества полиномов, для которых degφ(x)=m .
ГПТП, применяемые для последовательных схем.
Более жесткие требования к ГПТП необходимо предъявить в случае контроля правильности ф ункционирования последовательной схемы G, представляющей собой множество ф ункционально нез ависимых подсхем Gi, i={1,l}, имеющих ri входов и Vi выходов. Это объясняется тем фактом, что в случае последовательной схемы важна не только необходимость формиро - вания всевозможных входных наборов, но и последовательность их черед о - вания.
Минимальное требование с точки зрения пригодности последов а- тельной схемы — отсутствие колец обратной связи в режиме ко нтроля. Только в этом случае оказывается возможным опре делить необходимые условия, которым должен удовлетворять порождающий полином псевдосл у- чайной тестовой последовательности. Л юбую последовательн ую подсхему Gi схемы G, в которой отсутствуют кольца обратной связи, можно предст а- вить в виде уровней последовател ьно функционально связанных элементов памяти, их максимальное количество будет равняться ωi . Для исключения появления непроверяемых фрагментов в подобной подсхеме Gi необходимо использовать последовательности псевдослучайных тестовых наборов (л и - нейная зави симость между символами одного входного набора, а также вз а- имные линейные связи между символами последовательных наборов отсу т - ствуют). Другими словами, последовательность тестовых наборов, пре д - ставляющая собой псевдослучайные коды, должна иметь требуемую с тепень равномерного закона распределения, которая определяется величиной ωi.
