
C1 2012 корянов
.pdf
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
arccos 11 или arccos( 1) верно. 11
Следовательно, данное уравнение имеет единственное решение x 5.
Ответ: 5.
Использование ограниченности функций
Для использования ограниченности функции необходимо уметь находить множество значений функции и знать
оценки |
области значений |
|
стандартных |
||
функций |
(например, |
|
1 sin x 1; |
||
0 cos2 x 1; |
|
|
|
||
|
|
|
|
|
|
asin x bcosx a2 |
b2 |
|
и т.д.). |
||
метод оценки
Этот метод применяется при решении уравнений f (x) g(x), в которых его левые и правые части на всей ОДЗ удов-
летворяют |
неравенствам |
f (x) |
M , |
|||
|
g(x) |
|
M . |
В этом случае |
уравнение |
|
|
|
|||||
|
f (x) g(x) |
равносильно совокупности |
||||
систем: |
|
f (x) M, |
f (x) M, |
|
и |
g(x) M |
g(x) M. |
Соответственно, решив по отдельности каждое из уравнений приведенных систем, в дальнейшем нужно отобрать их общие решения.
Отметим, что метод оценки удобно использовать и при отборе корней уравнения.
Пример 56. Решить уравнение
3(
 3 sin12 x)(
3 sin12 x)(
 3 sin12 x) 27 (4x 5)2 .
3 sin12 x) 27 (4x 5)2 .
Решение. Оценим левую часть данного уравнения, начиная с выражения
|
|
|
|
|
|
|
|
( 3 sin12 x)( |
|
3 sin12 x) 3 sin2 12 x . |
|||||
Так как |
0 sin2 12 x 1, то последова- |
||||||
тельно |
получаем |
1 sin2 12 x 0, |
|||||
|
2 3 sin2 12 x 3, |
9 33 sin212 x 27. |
|||||
Для правой |
части |
имеем (4x 5)2 0, |
|||||
|
27 (4x 5)2 |
27 |
при всех значениях |
||||
x R. Равенство возможно только в том
случае, если обе части уравнения равны 27, то есть исходное уравнение равносильно системе
33 sin212 x 27
27 (4x 5)2 27.
Второе уравнение имеет один корень
x 5, который удовлетворяет и первому
4
уравнению системы.
Ответ: 1,25.
Пример 57. Решить уравнение
cos
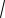 2 x2
2 x2  3 . 2
3 . 2
Решение. Рассматривая данное уравнение как простейшее тригонометрическое уравнение, получим

 2 x2 2 n, n Z. 6
2 x2 2 n, n Z. 6
Так |
как |
2 x2 |
2, |
то |
0 
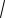 2 x2
2 x2 
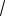 2.
2.
Из всех чисел вида 2 n, n Z, 6
отрезку [0;
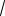 2] принадлежит только чис-
2] принадлежит только чис-
ло . Поэтому последнее уравнение рав- 6
носильно уравнению
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
2 x2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
6 |
|
|
|
|
|
|
|
|
|
|||||||
Возведя обе части уравнения в квад- |
|||||||||||||||||
рат, получим |
|
|
|
|
|
|
|
|
|||||||||
x2 2 |
2 |
2 |
|||||||||||||||
|
, откуда x 2 |
|
|
. |
|
|
|
||||||||||
36 |
36 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Ответ: |
|
|
|
|
2 |
||||||||
|
|
|
|
|
2 |
|
. |
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|||||
ограниченность синуса и косинуса |
|||||||||||||||||
Пример 58. Решить уравнение |
|
|
|
|
|
|
|
||||||||||
|
cos4x sin |
5x |
2. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Перепишем уравнение в ви- |
|||||||||||||||||
де cos4x 2 sin 5x . Так как при любом
3 |
|
5x |
|
|
значении x cos4x 1, а |
2 sin |
1, то |
||
|
||||
|
3 |
|
||
25.12.2011 www.alexlarin.net |
31 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
равенство cos4x 2 sin 5x может вы- 3
полняться в том и только в том случае, когда
cos4x 1, |
|
n |
|
|
|
|
||
x |
|
, n Z, |
|
|||||
2 |
|
|||||||
|
5x |
|
|
|
|
|
|
|
|
|
|
3 |
|
6 m |
|
|
|
sin |
|
1 |
|
|
|
|
||
|
|
|
|
|||||
|
3 |
|
x |
|
|
|
, |
m Z. |
|
10 |
5 |
||||||
|
|
|
|
|
|
|
||
Найдем такие целые значения n и m, |
||||||||
что |
n |
|
3 |
|
6 m |
, т.е. 5n 3 12m. Вы- |
|
|
|
||||
2 |
10 |
5 |
|
|||
ражая из последнего равенства n, полу-
чаем n 2m 2m 3. Так как n – целое, 5
то последнее равенство возможно, если
2m 3 |
делится |
на |
5, |
т.е. |
||
2m 3 5k, k Z. |
|
|
Отсюда |
|||
m 2k 1 |
k 1 |
. Поскольку |
m |
должно |
||
|
||||||
|
|
2 |
|
|
|
|
быть целым, то k |
должно быть нечет- |
|||||
ным. Если |
k 2p 1, где |
p Z, то |
||||
m 2(2p 1) 1 (2p 1) 1 5p 1. Сле- 2
довательно,
x 3 6 (5p 1) 3 6 p. 10 5 2
Ответ: 3 6 p, p Z. 2
Пример 59. Решить уравнение sin7x cos4x 1.
Решение. Воспользовавшись формулой преобразования произведения синуса и косинуса в сумму, приводим уравнение к виду sin11x sin3x 2, откуда получим sin11x 2 sin3x. Так как при лю-
бом значении |
x |
sin11x 1, а |
2 sin3x 1, |
то |
равенство |
sin11x 2 sin3x может выполняться в том и только в том случае, когда
|
|
|
|
|
|
2 n |
|||
sin11x 1, |
x |
|
|
|
|
|
|
, n Z, |
|
22 |
11 |
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
2 m |
|
|
||
2 sin3x 1 |
|
|
|
|
|
||||
|
x |
|
|
|
|
|
, m Z. |
||
|
6 |
|
|
3 |
|||||
|
|
|
|
|
|
|
|
||
25.12.2011 www.alexlarin.net |
32 |
Найдем такие целые значения n и m,
при которых |
|
|
|
2 n |
|
|
|
2 m |
т.е. |
||
|
|
|
|
|
|||||||
|
22 |
11 |
6 |
3 |
|
|
|||||
3n 2 11m. |
Выражая |
из |
последнего |
||||||||
равенства n, |
получаем |
n 3m |
2m 2 |
. |
|||||||
|
|||||||||||
|
|
|
|
|
|
|
3 |
|
|||
Так как n - целое, то последнее равенство возможно, только если 2m 2 делится на 3, т.е. 2m 2 3k, k Z. Отсюда
m 1 k k . Поскольку m должно быть
2 |
|
|
|
целым, то k |
должно быть четным. Если |
||
k 2p, |
где |
p Z, |
то |
m 1 2p 2p 3p 1. Следовательно, 2
x 2 (3p 1) 2 p . 6 3 2
Ответ: 2 p, p Z. 2
применение классических неравенств
Рассмотрим классическое неравенство Коши, известное школьнику как неравенство между средним арифметическим и средним геометрическим неотрицательных чисел, которое эффективно может быть использовано при решении уравнений.
Неравенство Коши для случая трех неотрицательных чисел
a b c 3
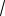 abc , 3
abc , 3
где равенство достигается при a b c, можно переписать в виде
a b c 33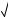 abc .
abc .
Для случая двух неотрицательных чисел неравенство
a b 
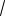 ab, 2
ab, 2
где равенство достигается при a b,
можно переписать в виде a b 2
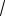 ab . Отметим частные случаи неравенства
ab . Отметим частные случаи неравенства
Коши для двух неотрицательных чисел: a b 2 при a 0, a 1 2 при a 0;
b a |
|
|
b |
|
a |
|
при a 0 |
|
a |
1 |
|
2. |
|
|
|
|||||
a |
||||||
|
|
|
|
|

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Пример 60. Решить уравнение
tgx ctgx 2cos8x .
Решение. Оценим левую и правую
части данного уравнения. |
|
1 |
|
|||||||
|
Так |
|
как |
tgx ctgx tgx |
, то |
|||||
|
||||||||||
|
|
|
|
|
|
|
|
tgx |
||
|
tgx ctgx |
|
2. В то |
же |
|
время |
||||
|
|
|
||||||||
|
2cos8x |
|
2. |
Значит, |
равенство |
|||||
|
|
|||||||||
tgx ctgx 2cos8x выполняется только в двух случаях:
1. |
tgx ctgx 2, |
или 2. |
tgx ctgx 2, |
|
|
||
|
2cos8x 2 |
|
2cos8x 2. |
1. Из первого уравнения последова-
тельно находим: |
2 |
2, |
sin 2x 1 |
, |
||||
|
||||||||
|
|
|
|
sin 2x |
|
|
||
x |
n, |
n Z ; из второго: |
cos8x 1 |
, |
||||
|
||||||||
4 |
|
|
|
|
|
|
||
x k , k Z. Нетрудно убедиться (на- 4
пример, воспользовавшись моделью тригонометрической окружности), что первое множество значений x содержится во
втором, и, значит, n , n Z, – реше-
ние системы. |
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
|
Решение |
первого |
|
уравнения |
||||||||
x |
|
n, n Z , второго |
x |
|
|
|
k |
, |
|||||
|
|
4 |
|||||||||||
4 |
|
|
|
|
|
8 |
|
|
|
||||
k Z. |
Равенство |
|
|
n |
|
|
k |
, |
т.е. |
||||
|
8 |
|
|||||||||||
|
|
|
4 |
|
4 |
|
|
|
|
||||
8n 3 2k , невозможно ни при каких целых значениях n и k (в его левой части стоит четное, а в правой – нечетное число). Следовательно, эта система решений не имеет.
Ответ: n,n Z. 4
Использование монотонности функций
При использовании монотонности функций различают случаи, когда функции, стоящие в обеих частях неравенства, имеют одинаковую монотонность или разную монотонность.
монотонность функции на множестве R
|
Если функция |
f (t) |
строго возрастает |
||
на |
R, то |
f h(x) f g(x) |
равносильно |
||
уравнению h(x) g(x). |
|
|
|||
|
Если функция |
f (t) |
строго убывает на |
||
R, |
то |
f h(x) f g(x) |
равносильно |
||
уравнению h(x) g(x). |
|
|
|||
Пример 61. Решите уравнение sin x 3sin x 2 (
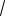 3 sin x) 3
3 sin x) 3
 3 2 sin x .
3 2 sin x .
Решение. Пусть sin x t. Рассмотрим функцию f (t) t 3t 2 , определенную при всех действительных значениях t.
Тогда данное уравнение примет вид
f (sin x) f (
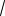 3 sin x).
3 sin x).
Функция f (t) строго возрастает на R как произведение двух возрастающих функций.
Следовательно, исходное уравнение равносильно уравнению sin x 
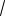 3 sin x
3 sin x
или sin x |
3 |
, решением которого яв- |
||||||
|
||||||||
2 |
|
|
|
|
|
|||
ляются значения x ( 1)n |
n, |
n Z. |
||||||
|
|
|||||||
3 |
|
|
|
|||||
|
Ответ: ( 1)n |
|
n, |
n Z. |
||||
|
|
|||||||
3 |
|
|
||||||
монотонность функции |
|
|||||||
на промежутке |
|
|||||||
Если функция f (t) строго монотон- |
||||||||
на на своей области существования – промежутке М, то уравнение f h(x) f g(x) равносильно системе
h(x) g(x)
E(h) M
E(g) M
Пример 62. Решить уравнение
arcsin(3x2 2x) arcsin(3x 2).
Решение. Перейдем к равносильной системе
|
2 |
2x 3x 2, |
|
2 |
5x 2 0, |
3x |
|
3x |
|
||
|
|
|
|
|
|
1 3x 2 1 |
1 3x 2 1 |
||||
25.12.2011 www.alexlarin.net |
33 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
|
x 2 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|||
|
x |
|
x |
|
. |
|
3 |
3 |
|||||
|
|
|
|
1 3x 2 1
Ответ: 1 . 3
Пример 63. Решить уравнение
arccos(x2 3) arccos(x 3).
Решение. Уравнение равносильно системе
|
2 |
3 x 3, |
|
2 |
x 6 0, |
x |
|
x |
|
||
1 x 3 1 |
4 x 2 |
||||
|
x 2 |
|
|
|
x 2. |
x 3 |
||
|
|
|
|
4 x 2 |
Ответ: 2. |
|
|
Пример 64. Решить уравнение
arccosx arcsin 2x .
Решение. Область допустимых значений уравнения определяется условиями x 1, 2x 1, т.е. | x | 0,5. Более того,
поскольку значения арккосинуса ограничены отрезком 0, , а арксинуса – отрез-
|
|
|
|
|
|||
ком |
|
|
; |
|
|
, то равенство левой и пра- |
|
2 |
2 |
||||||
|
|
|
|
|
|||
вой частей уравнения возможно только в случае, если их значения лежат на отрез-
|
|
|
|
||
ке |
0; |
|
|
, т.е. с учетом области допусти- |
|
2 |
|||||
|
|
|
|
||
мых значений при 0 x 0,5.
Таким образом, решение уравнения следует искать на множестве 0 x 0,5.
Так как функция y cost |
|
убывает на от- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
резке 0; |
|
, то на отрезке 0;0,5 |
уравне- |
|||||||
|
||||||||||
|
2 |
|
|
|
|
|
|
|
||
ние |
arccosx arcsin 2x |
|
|
|
равносильно |
|||||
уравнению |
cos arccosx |
cos arcsin 2x , |
||||||||
которое, в свою очередь, |
на 0;0,5 рав- |
|||||||||
|
|
|
|
|
|
x |
|
|
||
носильно |
уравнениям: |
|
|
|
1 4x2 , |
|||||
x2 1 4x2 , 5x2 1, x |
1 |
|
. |
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
5 |
|
|
|
|
|
|
Ответ: |
1 |
|
. |
||||
|
|
|
|
|
||||
y |
5 |
|
|
|||||
|
|
|
|
|||||
|
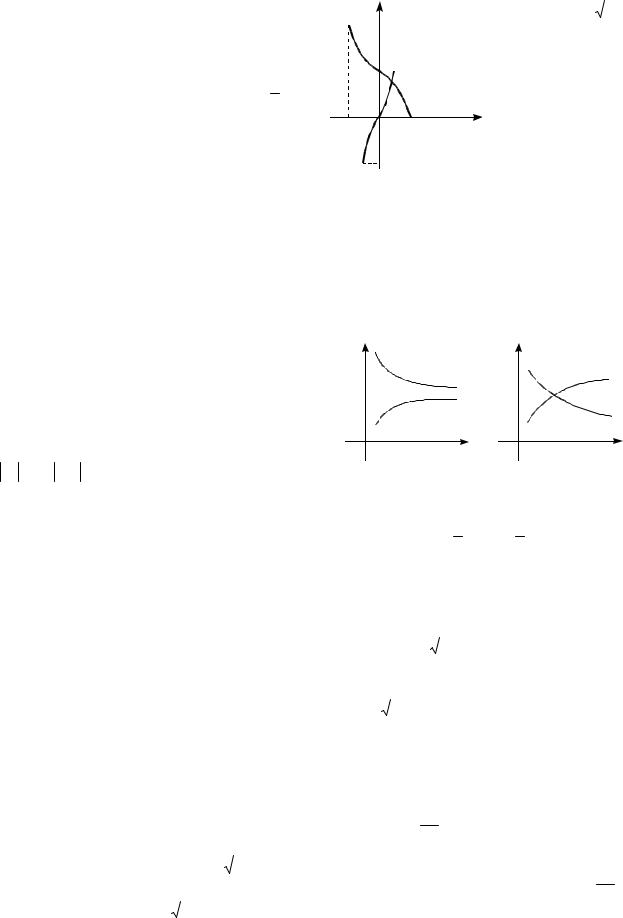
Замечание. |
|||||||
y = arccos x |
Процесс |
решения |
||||||
|
||||||||
уравнения в |
этом |
|||||||
|
примере |
можно |
||||||
-0,5 0,5 |
сделать |
нагляд- |
||||||
-1 O 1 |
x ным, |
построив |
||||||
y = arcsin 2x |
графики |
функций |
||||||
|
y arccos x |
|
|
и |
||||
Рис. 23 |
y arcsin2x |
(рис. |
||||||
23). |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
функции разной монотонности |
||||||||
Уравнение u(x) v(x), где u(x) |
– возрас- |
|||||||
тающая, а v(x) – убывающая функции, либо не имеет решений (рис. 24а), либо имеет единственное решение (рис. 24б).
y |
|
y |
|
v(x) |
|
|
v(x) |
|
|
|
|
u(x) |
|
|
u(x) |
O |
x |
O |
x |
а б
Рис 24
Пример 65. Найти корни уравнения cosx 
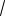 3ctgx
3ctgx 
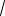 3sin x
3sin x
|
|
|
3 |
||
на промежутке |
2 ; |
|
. |
||
|
|||||
|
|
|
2 |
||
Решение. |
|
|
Функция |
||
f (x) cosx |
|
|
|||
3ctgx монотонно убывает |
|||||
на данном промежутке, как сумма убы-
вающих |
|
функций. |
Функция |
g(x) |
|
|
возрастает на |
3sin x монотонно |
|||
этом промежутке. Значит, исходное урав-
нение на промежутке |
|
2 ; |
3 |
имеет |
|
|
|
|
|||
|
|||||
|
|
|
2 |
|
|
не более одного корня. Легко проверить,
что число 5 является корнем данного
3
уравнения.
Ответ: 5 . 3
25.12.2011 www.alexlarin.net |
34 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Использование периодичности функций
Поскольку тригонометрические функции не являются монотонными на всей области определения, то равенство значений синусов, косинусов, тангенсов или котангенсов неравносильно равенству аргументов. Из монотонности функции на некотором промежутке и ее периодичности нетрудно показать следующие равносильности:
α β 2 n, |
||||
sinα sinβ |
|
|
(1) |
|
α β 2 n |
||||
α β 2 n, |
||||
cosα cosβ |
|
|
(2) |
|
α β 2 n |
||||
α β n, |
||||
|
|
|
(3) |
|
tgα tgβ |
|
|||
α |
|
|
m |
|
2 |
||||
|
|
|||
α β 2 n, |
||||
ctgα ctgβ |
|
|
(4) |
|
α m |
||||
(во всех формулах m,n Z). |
||||
Заметим также, что уравнения вида |
||||
sin f x cosg x |
и |
tg f x ctgg x с |
||
помощью формул приведения сводятся к уравнениям-равенствам одноименных функций:
|
|
|
|
|||
sin f x sin |
|
|
|
g x |
, |
|
|
|
|||||
|
2 |
|
|
|||
|
|
|
|
|
||
tg f x tg |
|
|
|
g x . |
|
|
|
|
|
|
|||
2 |
|
|
||||
Пример 66. Решить уравнение
sin x cos7x.
Решение. Используя тождество
|
|
|
||
cos7x sin |
|
7x |
, |
|
2 |
||||
|
|
|
||
перепишем |
уравнение |
в |
виде |
||
|
|
|
|
|
|
sin x sin |
|
7x |
. Применив равносиль- |
||
|
|||||
2 |
|
|
|
|
|
ный переход (1), сведем решение уравнения к решению совокупности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
7x 2 n, |
|
|
||||||||||
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
где n Z. |
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
7x |
2 n, |
|
|
||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В результате получим две серии реше- |
||||||||||||||
ний: |
x |
|
|
n |
|
или x |
|
|
n |
, |
||||
|
|
|
|
|
3 |
|||||||||
|
|
|
16 |
4 |
|
12 |
|
|
||||||
n Z.
Заметим, что вторую серию решений
можно также задать в виде x n . 12 3
Знак перед дробью n не имеет значе- 3
ния, поскольку параметр n пробегает все целые значения.
Ответ: |
|
|
n |
, |
|
|
|
n |
, |
|
|
12 |
|
||||||
16 |
4 |
|
3 |
|
|||||
|
|
|
|
|
|
|
n Z. |
||
Пример 67. Решить уравнение
tgx tg3x.
Решение. Применив равносильный переход (3), получим
x 3x n, |
|
|
n |
|
|||
x |
|
, |
|||||
2 |
|||||||
|
|
|
|
|
|
||
tgx tg3x |
|
|
|
|
|
||
x |
|
m, |
|
|
|
||
|
|
|
|||||
|
2 |
|
x |
2 |
m, |
||
|
|
|
|
|
|
||
где m,n Z. |
|
|
|
||||
Заметим, что |
если |
n 2m 1, где |
|||||
m Z, то соответствующие значения x попадают в разряд «запрещенных», поскольку в этом случае x (2m 1) m.
2 |
2 |
|
При n 2m, где |
m Z, получаем ре- |
|
шения вида x m. Полученные решения можно записать как x m так как m Z.
Ответ: x m, m Z.
Замечание. Уравнения, представляющие собой равенства синусов или косинусов, можно решать иначе: путем преобразования разности синусов или косинусов в произведение.
Пример 68. Решить уравнение
cos2x cosx 0.
25.12.2011 www.alexlarin.net |
35 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Решение. По формуле преобразования суммы косинусов в произведение получим
|
2sin |
x |
sin |
3x |
|
|
0. |
|
|||||
|
|
|
|
|
|||||||||
|
2 |
|
2 |
|
|
|
|
||||||
Отсюда |
имеем |
sin |
x |
|
0, |
x 2 n, |
|||||||
|
|||||||||||||
|
|
3x |
|
|
|
2 |
|
2 k |
|
||||
n Z или |
sin |
0, |
x |
, k Z. |
|||||||||
|
|
||||||||||||
|
2 |
|
|
|
3 |
|
|||||||
Заметим, что первая серия решений включается во вторую.
Использование четности
инечетности функций
Если функция f (x), определенная на
некотором промежутке X , является на этом промежутке возрастающей или убывающей и принимает на X множество значений Y , то для каждого числа a Y
найдется |
единственное значение x0 X |
||
такое, что |
f (x0 ) a. |
|
|
Следствие 1. Если нечётная функция |
|||
f (x) является возрастающей |
или убы- |
||
вающей при x 0, |
то для каждого числа |
||
a E( f ) уравнение |
f (x) a имеет один |
||
корень. |
|
|
|
Следствие 2. Если чётная |
функция |
||
f (x) является возрастающей |
или убы- |
||
вающей при x 0, |
то для каждого числа |
||
a E(f ) |
уравнение f (x) a имеет два |
||
корня x1 , |
x2 , где x1 x2 , если |
a f (0); |
|
и один корень x0 0, если a f (0).
Пример 69. Решить уравнение
x10 (12x 13)5 23sin(12x 13) 23sin x2 .
Решение. Приведём исходное уравнение к виду
x10 23sin x2 (12x 13)5 23sin(12x 13).
Рассмотрим непрерывную функцию f (t) t5 23sint . Данная функция определенная для любого значения аргумента, нечётная, так как f ( t) ( t)5 23sin( t) (t5 23sint)
f (t). |
Найдём |
её производную: |
||||
f |
|
(t) 5t |
4 |
23cost . |
Покажем, |
что |
|
|
|||||
f |
|
|
на всей области определения. |
|||
|
(t) 0 |
|||||
|
|
|
|
|
||
При t |
|
|
; |
|
|
: |
2 |
|
|||||
|
|
|
2 |
|
||
f |
|
|
4 |
23cost 3 0 |
2 |
23 0 0 0 0, |
|||||
(t) 5t |
|
|
|||||||||
а при | t | |
|
|
: |
|
|
|
|
||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
||
|
f |
(t) 5t |
|
23cost 3 |
|
|
23 ( 1) |
||||
|
|
|
|||||||||
2
4
5 3 23 25162 23 0.2
Следовательно, f (t) возрастает на всей числовой прямой. Значит, каждое своё значение функция принимает в точности при одном значении аргумента, а стало быть, уравнение f (t1) f (t2 ) равносильно уравнению t1 t2 . Записав исходное урав-
нение в виде f (x2) f (12x 13) , получим f (x2 ) f (12x 13) x2 12x 13
x2 12x 13 0 |
x 13, |
|
|
|
x 1. |
|
Ответ. 1; 13. |
Пример 70. (ЕГЭ-2009, С5). Решить |
|
уравнение |
|
87cos(x2 ) (8 6x)4 x8 |
87cos(8 6x) . |
Решение. Приведём исходное уравне- |
|
ние к виду |
|
x8 87cos(x2 ) (8 6x)4 |
87cos(8 6x). |
Рассмотрим непрерывную функцию f (t) t4 87cost. Данная функция определена для любого значения аргумента, чётная, так как f ( t) f (t). Найдём её производную: f (t) 4t3 87sint .
При t (0; ):
|
|
3 |
87sint |
0 0 0, |
|||||
f (t) 4t |
|
||||||||
а при t [ ; ): |
|
|
|
|
|
|
|||
|
|
|
3 |
87sint 4 |
3 |
87 |
|||
f (t) 4t |
|
|
|||||||
4 33 87 4 27 87 0. |
|
||||||||
Таким |
образом, |
|
|
|
при |
||||
f |
(t) 0 |
||||||||
t (0; ), |
следовательно, |
f (t) |
возрас- |
||||||
тает на промежутке [0; ). Значит, каждое своё значение из множества значений E(f ), кроме f (0), функция принимает в двух симметричных относительно
25.12.2011 www.alexlarin.net |
36 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
t 0 |
точках, |
а |
стало |
быть, |
уравнение |
|||
f (t1) f (t2 ) |
равносильно |
уравнению |
||||||
|t1 | |t2 |. Записав исходное уравнение в |
||||||||
виде |
f (x2 ) f (8 6x), получим |
|
||||||
f (x2 ) f (8 6x) |
x2 |8 6x | |
|
||||||
|
x2 |
8 6x, |
|
x2 |
6x 8 0, |
|||
|
6x 8; |
|
|
|
|
|||
|
x2 |
|
x2 |
6x 8 0; |
||||
|
|
|
|
|
|
|
|
|
x 3 
 17,
17,
x 3  17,
17,
x 2,
x 4.
Ответ: 3 
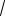 17 ; 3
17 ; 3 
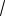 17 ; 2; 4.
17 ; 2; 4.
Тренировочные упражнения
74.Решите уравнение tg2x ctg5x .
75.Решите уравнение ctg3x ctgx.
76.Дано уравнение cos2x cosx 0. а) Решите уравнение.
б) Укажите корни, принадлежащие от-
5
резку 0; .
2
77. Дано уравнение cos6x cos3x 0. а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку 0; .
78.Укажите наибольший корень уравнения cos2x 3sin x 2, принадлежащий отрезку [ 3 ; ].
79.Укажите наименьший корень уравнения cos2x 2 3cosx, принадлежащий отрезку [ 2,5 ; 0,5 ].
Решите уравнение:
80.cos3x cos2x 1.
81.sin3x cos2x 1.
|
|
|
|
|
|
|
|
13x |
|
|
|
|
|
|
|||
82. |
|
|
|
|
|
|
|
|
x |
|
|||||||
cos |
22 |
|
|
|
3 |
|
|
|
. |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
11x |
|
|
33 |
|
||||||
83. |
|
x |
|
|
|
|
|
|
|||||||||
2 |
|
|
sin |
|
|
|
|
|
|
. |
|||||||
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||
84. |
2cos( x ) |
x2 |
6x 11. |
||||||||||||||
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
85. |
x |
2 |
|
x2 |
4x 7. |
||||||||||||
3 |
|
|
|
|
|||||||||||||
86.cosx 1 x2 4 x 4 2 .
87.x2 x 2 sin x 1. 4
88. x2 6x 10 sin 3 x . 2
89.x2 4x 5 cos4 x.
90.| cos((x 2)cosx)|
1 |log4 (9x2 39x 43) |.
91. |
2cosx |
x |
2 |
|
3 |
x |
2 |
|
2. |
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
92. |
3sin x |
|
x2 |
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
93. |
arcsin(2x3 2x2 |
3x 0,2) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
arcsin(3x2 |
2x 0,2) . |
|||||||||||||||||||||||||||||||
94. |
arccos(2x3 |
5x2 |
x 0,2) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
arccos(2x 4x2 |
0,2) . |
|||||||||||||||||||||||||||||||
95. |
arctg(4x2 8x 9) arctg16x2 |
|
0. |
||||||||||||||||||||||||||||||||||
96. |
log2 (x2 |
4x 8) sin |
|
5 x |
|
cos |
x |
. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|||||||||||||
97. |
log3 (x2 |
4x 13) |
cos x sin |
|
x |
. |
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||
98. |
|
x2 (2 5 )x 6 2 4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin(x 13 ) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
99. |
|
x2 (3 )x 6 2 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
0. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
100. sin x cos x 2log |
3 x |
2 |
|
1 |
x |
49 |
. |
|
|
||||||||||||||||||||||||||||
|
2 |
16 |
|
|
|||||||||||||||||||||||||||||||||
101.
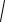 (x 1)2 16 4 sin2 x .
(x 1)2 16 4 sin2 x .
102.98cos(x2) (4x 3)4
x8 98cos(4x 3).
103.23cos(x2) 23cos(12 8x)
x6 |12 8x |3 .
2.5. Комбинированные уравнения
Решение комбинированных уравнений представляет определенные трудности для учащихся. При решении этих уравнений применяют различные методы решения.
Уравнения, содержащие дроби
Пример 71. Решить уравнение
cosx 0. 1 sin x
25.12.2011 www.alexlarin.net |
37 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Решение. Данное уравнение равносильно системе
cosx 0, |
|
cosx 0, |
|||||
|
|
|
|
|
|||
1 sin x 0 |
|
sin x 1. |
|||||
Если cosx 0, то из основного триго- |
|||||||
нометрического тождества |
sin x 1 или |
||||||
sin x 1 |
. Так как |
sin x 1, |
то остается |
||||
отобрать |
те значения |
x, при |
которых |
||||
sin x 1 |
. Отсюда x |
|
2k , |
k Z. |
|||
2 |
|||||||
|
|
|
|
|
|
||
Ответ: 2k , k Z. 2
Пример 72. Решить уравнение
cosx 1. 1 sin x
Решение. Область допустимых значений уравнения определяется условием 1 sin x 0. На ОДЗ исходное уравнение равносильно следующим:
cosx sin x 1 0; cosx sin x 1 0;
|
|
1 sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
cos x |
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
||||||||
Из |
последнего |
|
уравнения находим |
|||||||||||||||||
x |
|
|
|
2 n или |
|
x |
|
|
|
2 n, от- |
||||||||||
|
|
|
|
|
||||||||||||||||
4 |
4 |
|
|
|
4 |
4 |
|
|||||||||||||
куда x 2 n или x |
|
2 n. |
||||||||||||||||||
|
||||||||||||||||||||
Если x 2 n, то |
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
sin x 1 sin 2 n 1 1; |
||||||||||||||||
если x |
|
2 n, то |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
sin x 1 sin |
|
|
|
2 n 1 0. |
||||||||||||||
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, числа 2 n входят, а чис-
ла 2 n не входят в область допус-
2
тимых значений исходного уравнения.
|
Ответ: 2 n, |
n Z. |
|
Пример 73. Решить уравнение |
|
||
|
cosx sin 2x |
1. |
|
|
|
|
|
|
cos3x |
|
|
Решение. Общий наименьший поло- |
|||
жительный период функций |
cosx, |
||
cos3x, sin 2x равен 2 . Поэтому достаточно рассмотреть решения уравнения на промежутке [0;2 ).
Умножим обе части уравнения на cos3x 0. Далее получаем
|
|
|
|
cosx sin 2x cos3x |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
cos3x cosx sin 2x 0 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2sin 2xsin x sin 2x 0 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2x 0, |
|
|
|
|||||||||
sin 2x(2sin x 1) 0 |
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
2 l, |
k,l, m Z. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 m, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
На промежутке [0;2 ) содержатся кор- |
|||||||||||||||||||||||||||||||||
ни 0, |
|
, |
|
, |
|
3 |
, |
|
7 |
, |
|
11 |
. Из условия |
||||||||||||||||||||
|
|
|
2 |
|
6 |
|
|
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
n |
|
|
|
|
|
|
|
|
||||||||||
cos3x 0 |
получаем x |
|
|
|
,n Z, а |
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
||||
на промежутке [0;2 ) – |
|
x |
|
, |
x |
|
, |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
2 |
|
|
x |
5 |
, |
x |
7 |
, |
x |
3 |
, |
x |
11 |
. |
Таким |
|||||||||||||||||||||
|
6 |
|
|
|
|
||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
||||||||||
образом, остались числа 0 и , а значит,
исходное уравнение |
имеет множество |
||||
корней x t, t Z. |
|
||||
|
|
|
|
|
Ответ: t, t Z. |
|
Пример 74. Решить уравнение |
||||
|
|
|
|
ctgx tg2x 0. |
|
|
Решение. |
Имеем |
последовательно |
||
|
1 |
|
2tgx |
0, 1 tg2 x 0. Последнее |
|
|
|
1 tg2 x |
|||
|
tgx |
|
|
||
уравнение не имеет корней. При замене
выражения ctgx на выражение 1 и при tgx
замене выражения tg2x на выражение может произойти потеря корней
n, n Z. Проверкой убеждаемся, 2
25.12.2011 www.alexlarin.net |
38 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
что числа этого вида являются корнями исходного уравнения.
Ответ: n, n Z.
2 |
|||||
Пример 75. Решить уравнение |
|||||
|
tg5xtg8x 1. |
|
|||
Решение. tg5xtg8x 1 |
|||||
|
sin5x |
|
sin8x |
1 |
|
|
|
|
|||
|
cos5x cos8x |
|
|||
cos8xcos5x sin8xsin5x 0, |
|||||
|
|
||||
cos8x 0, |
|||||
|
|
||||
cos5x 0; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
, |
|
|
n Z, |
||
|
cos3x 0, |
|
6 |
|
|
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||||||
|
cos8x 0, |
|
x |
|
|
|
|
|
|
|
|
, |
k Z, |
||||||
16 |
8 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
cos5x 0; |
|
|
|
|
|
|
|
|
m |
|
||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
, |
m Z. |
|||
|
|
|
|
|
|
10 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|||||||
Выясним, |
какие |
|
из |
|
|
|
|
значений |
|||||||||||
x |
|
|
n |
, n Z , |
являются недопусти- |
||||||||||||||
6 |
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
мыми. Для этого решим в целых числах
уравнения |
|
|
|
|
|
|
|
|
n |
|
|
|
k |
|
и |
||||||||||
6 |
3 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
16 |
8 |
|
|
||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
m |
. |
|
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
10 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Рассмотрим |
|
|
|
|
|
уравнение |
||||||||||||||||
|
|
|
n |
|
|
|
k |
. После |
преобразований |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
6 |
3 |
16 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
получим: 8 16n 3 6k |
6k 16n 5. |
|
|||||||||||||||||||||||
Последнее равенство невозможно, так как в левой его части стоят четные числа, а в правой – нечетное.
Рассмотрим уравнение
n m . 6 3 10 5
После преобразований получим: 5 10n 3 6m 3m 5n 1
m 5n 1 m 2n n 1. 3 3
Поскольку m и n – целые числа, то n 1 3t , где t Z. Таким образом, n 3t 1 – недопустимые значения. Итак,
x n , n Z и n 3t 1 (t Z). 6 3
Заметим, что в этой задаче форму записи ответа можно упростить. Для этого напомним, что при делении на 3 возможны только остатки 0, 1 или 2, т.е. любое целое число n представимо в одном из
трех видов: n 3t , |
n 3t 1 |
или n 3t 2 |
(t Z). Значит, |
либо |
n 3t , либо |
n 3t 2 . |
|
Получаются две серии реше- |
|||||
ний: x |
|
t и x |
|
|
5 |
t . Эти серии |
|
1 |
|
6 |
|
2 |
6 |
|
|
решений легко объединяются. Оконча-
тельно получаем: x l , l Z. 6
Ответ: l, l Z. 6
Иногда умножение на выражение с переменной является ключевым при решении некоторых уравнений, которые не имеют дробей.
Пример 76. Решить уравнение
8cosxcos2xcos4x 1.
Решение. Ключевым моментом в решении данного уравнения является умножение обеих частей уравнения на sin x. Проверим имеет ли исходное уравнение
корни уравнения |
sin x 0, то есть числа |
|||
n, n Z. |
Если |
n – |
четное, |
то есть |
n 2n1, то |
подставляя |
2 n1 , |
получаем |
|
ложное равенство 8 1. При нечетном n, то есть n 2n1 1, подставим 2 n1 . Получим также ложное равенство 8 1.
Преобразуем данное уравнение
8cosxcos2xcos4x 1 |
|
|
|||||
8sin xcosxcos2xcos4x sin x |
|
||||||
4sin 2xcos2xcos4x sin x |
|
||||||
2sin 4xcos4x sin x |
|
|
|||||
sin8x sin x 0 |
|
||||||
|
2 m |
|
|
|
|
||
x |
|
|
|
, |
|
|
|
|
7 |
|
m,k Z. |
|
|||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
2 k |
|
|
|||
x |
|
|
|
|
, |
|
|
9 |
|
9 |
|
|
|||
|
|
|
|
|
|
||
При умножении обеих частей уравнения на sin x могут появиться посторонние корни n, n Z.
25.12.2011 www.alexlarin.net |
39 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Для x |
2 m |
рассмотрим уравнение |
|
7 |
|||
|
|
2 m n или 2m 7n. Если n нечетное, 7
то есть n 2p 1, p Z, то равенство 2m 14p 7 невозможно (в левой части четное число, в правой – нечетное). Пусть
n 2p, |
p Z, |
|
|
|
тогда |
|
имеем |
||||||||
m 7p, |
|
|
p Z. |
|
Отсюда следует, что чис- |
||||||||||
ла вида |
|
|
2 m |
являются корнями данного |
|||||||||||
7 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнения, где m 7p, p Z. |
|
||||||||||||||
|
|
Если |
|
|
x |
|
|
2 k |
, |
то |
имеем |
||||
|
|
|
|
|
|
||||||||||
|
|
|
2 k |
|
|
|
9 |
9 |
|
|
|
||||
|
|
n |
или 1 2k 9n. |
Если n |
|||||||||||
9 |
|
||||||||||||||
9 |
то есть n 2t, t Z, то равенство |
||||||||||||||
четное, |
|||||||||||||||
1 18t 2k |
|
|
невозможно. |
Пусть |
|||||||||||
n 2t 1, t Z, |
|
тогда |
|
получаем |
|||||||||||
k 9t 4, t Z. |
|
|
|
|
|
||||||||||
Ответ: 2 m, m 7p; m, p Z;
7
2 k , k 9t 4; k, t Z. 9 9
Тренировочные упражнения
104. Решите уравнение
cosx sin2x 1. cos3x
105. Определите количество корней
уравнения 2sin x 
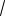 3 0 на промежут2cos x 1
3 0 на промежут2cos x 1
ке [ 3;5].
Решите уравнение:
|
cos |
x |
|
|
cos2x 1 sin x |
|
|||
|
|
|
|
|
|
||||
106. |
2 |
0. |
107. |
0. |
|||||
|
|||||||||
|
sin |
|
x |
|
|
ctgx 1 |
|||
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|||
108.cos2x cosx 1 0. 2sinx 
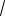 3
3
109.cos2x sin x 1 0. 2cosx 
 3
3
110.2 2cos2 x 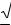 3sin x 0. tgx
3sin x 0. tgx 
 3
3
111. 2 2sin2 x 
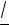 3cosx 0.
3cosx 0.
|
|
|
ctgx |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ctg |
|
|
|
x |
|
|
3tgx |
|
|
|
|||||||
2
112.0.
2cosx 1
113.
sin4x sin2x cos3x 2sinx 1 0.
2sin2x |
3 |
|
|
114. Найдите все значения x, при каж- |
|||
дом из которых |
выражения |
sin 4x |
и |
|
|||
|
|
tg2x |
|
cos4 x sin4 x принимают равные значеtg2x
ния.
Решите уравнение:
115.ctg2x cos5x sin x 0.
116.tg2x tg4x tg5x tgx.
117.sin3x 0. 118. 2sin x 
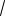 3 0.
3 0.
sin x |
2cosx 1 |
119.sin 2x cosx. tgx
120.1 cosx sin x 0. cosx
121.sin x cosx 0.
|
4x |
|
|
|||||
122. |
sin x cosx |
1. |
||||||
|
|
|
||||||
|
cosx cos3x |
|
|
|||||
123. |
4tg2x 3tgx |
|
0. |
|||||
5sin2x 3sin x |
||||||||
|
|
|
||||||
124. |
3ctg2x 4ctgx |
|
0. |
|||||
5cos2x 4cosx |
|
|||||||
|
|
|
||||||
125. |
cos4x |
|
sin 4x |
. |
||||
|
|
|||||||
|
sin 2x cos2x |
|
|
|||||
126.4cosx ctgx 4ctgx sin x 0.
127.3sin2x tgx 4cos2 x 7sin x 1.
128.Найдите сумму различных корней уравнения
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
4sin |
|
7 xcos |
|
7 x |
sin |
|
|
|
14 x |
|
|||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x |
|
|
|
|
|
|
|
|
||||
|
|
|
sin |
3 |
|
|
|
|
|
|
4 x |
|
|
|
|||||
|
|
|
2 |
|
|
|
|
5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
||
|
|
|
|
3 |
|
5 x |
|
|
|||||||||||
|
|
|
|
|
|
|
3 |
|
6 |
||||||||||
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
на отрезке [3;5].
25.12.2011 www.alexlarin.net |
40 |
