
C1 2012 корянов
.pdf
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
cos x 2 .
|
|
5 |
|
Его решения имеют вид |
|
||
x arccos |
2 |
2 n, |
n Z. |
|
|||
5 |
|
|
|
Подставляя arccos3 , имеем
5
x arccos2 arccos3 2 n, n Z .
5 |
5 |
|
|
|
|
||
Ответ: arccos |
2 |
|
arccos |
3 |
|
2 n, |
|
|
|
||||||
|
5 |
|
5 |
|
n Z . |
||
|
|
|
|
|
|
|
|
Уравнение вида |
acosx bsin x c, в |
||||||
случае, когда c 0, а коэффициенты a и b отличны от нуля, сводится к простейшему делением на cosx или sin x.
Пример 37. Решить уравнение sin x 5cosx 0 .
Решение. Среди значений x, для которых cosx 0, корней уравнения нет (если cosx 0, то из уравнения следует, что и sin x 0, а одновременно эти два равенства выполняться не могут). Значит, деление обеих частей уравнения на cosx не приведет к потере корней. Разделив, получим уравнение
tgx 5 0,
откуда x arctg5 n, n Z
Ответ: arctg5 n, n Z.
Пример 38. Решить уравнение
8sin3x 15cos3x 1.
Решение. Разделим обе части уравне-
ния на 
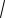 82 152 17. Уравнение примет вид
82 152 17. Уравнение примет вид
|
8 |
sin3x |
15 |
cos3x |
1 |
|
|
|
||||||||
17 |
|
|
|
|
||||||||||||
|
17 |
17 |
1 |
|
||||||||||||
sin3xcos cos3xsin |
|
|
|
|||||||||||||
17 |
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
sin(3x ) |
, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
17 |
|
|
|
|
|
|
||||
где cos |
8 |
, sin |
15 |
. Тогда имеем |
||||||||||||
|
|
|||||||||||||||
1717
x( 1)n arcsin 1 n; 17
x ( 1)n arcsin 1 n, n Z. 17
Так как cos 8 0, sin 15 0, 17 17
то угол лежит в четвертой четверти и
|
|
|
|
15 |
|
|
15 |
|
||||
поэтому arcsin |
|
|
|
|
arcsin |
|
. |
|||||
17 |
|
|||||||||||
|
|
|
|
|
|
17 |
|
|||||
Ответ: arcsin |
15 |
( 1)n arcsin |
|
1 |
n, |
n Z. |
||||||
|
17 |
|||||||||||
17 |
|
|
|
|
|
|
|
|
|
|||
Тренировочные упражнения
Решите уравнения:
21.
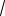 2sin x
2sin x 
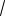 2cosx
2cosx 
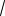 3 .
3 .
22.
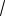 3sin x cosx
3sin x cosx 
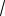 2.
2.
23.Дано уравнение

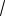 3sin 4x cos4x 0.
3sin 4x cos4x 0.
а) Решите уравнение.
б) Укажите корни, принадлежащие от-
|
|
|
|
|
|
|
|
||
резку |
|
|
; |
|
. |
|
|
||
2 |
|
|
|
||||||
24. |
|
2 |
|
|
|
||||
Найдите |
корни |
уравнения |
|||||||
sin3x cos3x, |
принадлежащие отрезку |
||||||||
[0;4]. |
|
|
|
|
|
|
|
|
|
25. |
Найдите |
корни |
уравнения |
||||||
sin 2x |
|
|
cos2x, принадлежащие отрез- |
||||||
|
3 |
||||||||
ку [ 1;6]. |
|
|
|
|
|
|
|||
26. |
Найдите |
корни |
уравнения |
||||||

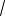 3sin 2x cos2x, принадлежащие отрез-
3sin 2x cos2x, принадлежащие отрез-
ку [ 1;4].
27. |
|
Найдите |
корни |
уравнения |
||
|
|
sin x cosx 1 |
на отрезке |
[ 3 ;3 ]. |
||
|
3 |
|||||
28. |
|
Найдите |
корни |
уравнения |
||
sin x |
|
cosx 1 |
на отрезке |
[ 2 ;4 ]. |
||
3 |
||||||
2.2. Тригонометрические уравнения, сводящиеся к алгебраическим уравнениям с помощью замены
В тех случаях, когда исходное урав-
нение может |
быть приведено |
к виду |
f (g(x)) 0, то |
заменой g(x) t |
уравне- |
ние сводится |
к решению уравнения |
|
f (t) 0. Далее для каждого полученного корня tk необходимо решить уравнение g x tk .
25.12.2011 www.alexlarin.net |
21 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
В тех случаях, когда множество значений функции g(x) известно, то пишется ограничение на новую переменную.
Например, |
|
sin x t |
при |
|
|
1 t 1, |
||||||||||
cosx t при |
1 t |
1, |
|
sin2 |
x t |
при |
||||||||||
0 t 1, |
cos2 x t |
|
при |
|
|
0 t 1, |
||||||||||
arcsin x t |
при |
|
|
t |
|
, |
arccosx t |
|||||||||
|
|
|||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|||
при 0 t , |
arctgx t |
при |
|
t |
, |
|||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||
arcctgx t при 0 t .
Иногда при решении уравнений часть «посторонних» решений возникающих в результате замены могут быть удалены по причине несоответствия их области определения или множеству значений тригонометрических и обратных тригонометрических функций. Напомним их.
Функция |
Область |
Множество |
||||||||||
определения |
значений |
|||||||||||
|
||||||||||||
y sin x |
( ; ) |
[ 1;1] |
||||||||||
y cosx |
( ; ) |
[ 1;1] |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
y tgx |
все x |
|
k , |
( ; ) |
||||||||
2 |
||||||||||||
|
k Z |
|
|
|
|
|
|
|
|
|||
y ctgx |
все |
( ; ) |
||||||||||
x k , |
||||||||||||
|
k Z |
|
|
|
|
|
|
|
|
|||
y arcsin x |
[ 1;1] |
|
|
|
|
|||||||
|
|
|
; |
|
|
|
||||||
2 |
|
|||||||||||
|
|
|
|
|
|
|
2 |
|||||
y arccosx |
[ 1;1] |
[0; ] |
||||||||||
y arctgx |
( ; ) |
|
|
|
|
|||||||
|
|
|
; |
|
|
|
||||||
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
2 |
||||
y arcctgx |
( ; ) |
(0; ) |
||||||||||
Покажем на примерах как ограничение, связанное с новой переменной, позволяет проводить проверку на промежуточном этапе решения.
Пример 39. Решить уравнение
2cos2 |
|
x |
15cos |
x |
8 0. |
||
2 |
|
||||||
|
2 |
|
|
|
|||
Решение. |
Обозначим cos |
x |
t, где |
||||
|
|||||||
|
|
|
2 |
|
|||
1 t 1. Полученное квадратное уравнение 2t2 15t 8 0 имеет корни
t1 |
|
1 |
и t |
2 8 (не удовлетворяет усло- |
||||||||||
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
вию 1 t 1). |
|
|
|
|
|
x |
|
1 |
|
|||||
|
Решая уравнение cos |
|
, получаем |
|||||||||||
|
|
|
||||||||||||
|
|
|
x |
|
1 |
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
arccos |
|
|
2 n, n Z, |
|||||||
|
2 |
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
x 2 |
arccos |
|
4 n, n Z, |
||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x 2 |
|
|
|
4 n, n Z, |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
x 4 4 n, n Z. 3
Ответ: 4 4 n, n Z. 3
Пример 40. Решить уравнение
arccos2 x 8arccosx 15 0.
Решение. Положим arccosx t. Так как множество значений функции arccosx – отрезок 0; , найдем решения
уравнения |
t2 8t 15 0, |
удовлетво- |
|
ряющие условию |
0 t . |
Такой корень |
|
один: t 3. |
Если |
t 3, то |
arccosx 3, |
откуда x cos3. |
|
|
|
Ответ: cos3.
Сведение тригонометрических уравнений к алгебраическим путем замены переменной – одна из наиболее плодотворных идей, используемая для решения тригонометрических уравнений. Рассмотрим несколько типичных ситуаций введения новой переменной.
уравнения, сводящиеся к многочлену от одной тригонометрической функции
Рассмотрим уравнения, сводящиеся к квадратным относительно синуса, косинуса, тангенса или котангенса.
Пример 41. Решить уравнение
2sin2 x cosx 1 0.
Решение. Используя основное тригонометрическое тождество, приведем уравнение к виду
2cos2 x 1 cosx 0 или (2cosx 1)(cosx 1) 0.
Отсюда
25.12.2011 www.alexlarin.net |
22 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
cosx 0,5, x 2 2 n, n Z, или
3
cosx 1, x 2 k, k Z.
Заметим, что все решения можно представить одной формулой
x 2 k , k Z.. 3
Ответ: 2 k , k Z. 3
Пример 42. Решить уравнение
2sin2 x 9cos x 3 0. 3 3
Решение. Воспользовавшись основным тригонометрическим тождеством, перепишем уравнение в виде
|
|
|
|
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|||||
|
|
|
2 1 cos |
|
|
|
|
|
|
9cos |
|
|
3 0, |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
или |
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2cos2 |
|
9cos |
5 0. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
Заменой cos |
x |
t |
|
уравнение сводится |
|||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
2t2 9t 5 0, которое |
|||||||||||||||||
к квадратному |
|
|
|||||||||||||||||||||||
имеет два корня: |
t |
|
1 |
и |
t |
|
5. Воз- |
||||||||||||||||||
|
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|||||
вращаясь |
к переменной |
x, |
получим: |
||||||||||||||||||||||
cos |
x |
|
1 |
|
и |
|
|
|
|
|
cos |
x |
5. |
|
|
Уравнение |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
cos |
x |
|
1 |
|
имеет |
корни |
x 6 n; |
||||||||||||||||||
|
|
||||||||||||||||||||||||
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение cos x 5 корней не имеет.
3 |
n Z. |
Ответ: 6 n, |
Замечание. Вводя новую перемен-
ную t cos x , можно было сразу учесть, 3
что значения косинуса ограничены отрезком [ 1;1], и, значит, интерес представ-
ляют только |
те корни уравнения |
2t2 9t 5 0, |
которые удовлетворяют |
условию t 1. Накладывать при замене
ограничения на новую переменную не обязательно, но во многих случаях – полезно, поскольку это иногда упрощает решение.
Пример 43. Найти все корни уравнения tgx 3ctgx 2 0, удовлетворяющие условию sin 2x 0.
Решение. Если записать условие sin 2x 0 в виде 2sin x cosx 0 , то ста-
новится очевидным, что оно выполняется в том и только в том случае, когда sin x и cosx имеют разные знаки, что в свою очередь равносильно условию tgx 0.
Введением новой переменной tgx t сведем исходную задачу к решению смешанной системы:
t 3 1 2 0, t 0, t
или
t2 2t 3 0, t 0.
Уравнение |
t2 2t 3 0 имеет два |
|||
корня |
t 3, |
t 1, из |
которых |
только |
первый |
удовлетворяет |
условию |
t 0. |
|
Возвратившись к исходной переменной, получим уравнение tg x 3. Следова-
тельно, x arctg3 n, n Z. |
|
Ответ: arctg3 n, |
n Z. |
решение уравнений, однородных относительно синуса и косинуса
Однородными относительно sin x и cosx называют уравнения вида,
an sinn x an 1 sinn 1 xcosx ...
... a1 sin xcosn 1 x a0 cosn x 0,
в которых сумма показателей степеней у sin x и cosx (степень уравнения) во всех членах уравнения одинакова. Например,
asin x bcosx 0 – однородное урав-
|
|
нение первой |
сте- |
|
|
|
пени, |
|
|
asin2 |
x csin xcosx bcos2 x 0 |
– од- |
||
|
|
нородное |
уравне- |
|
|
|
ние второй степе- |
||
|
|
ни, |
|
|
asin3 |
x csin2 |
xcosx dsin xcos2 |
x |
|
bcos3 x 0 – |
однородное |
уравнение |
||
|
|
третьей степени. |
|
|
Делением обеих частей уравнения на cosk x или sink x , где k – степень уравнения, однородные уравнения сводятся к
25.12.2011 www.alexlarin.net |
23 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
алгебраическим относительно t tgx или t ctgx.
Однако следует иметь в виду, что деление может привести к потере корней. Чтобы избежать этого, сначала требуется установить не являются ли корнями
уравнения числа вида x n, n Z, 2
при делении на cosk x , и, соответственно, числа вида x n, n Z, при делении
на sink x. Далее после делим на cosk x или sink x ищем другие решение уравнения, отличные от указанных.
В частности, уравнения вида
asin2 x csin xcosx bcos2 x d
приводятся к однородным путем представления правой части в виде:
d d (sin2 x cos2 x).
Пример 44. Решить уравнение
10cos2 x 5sin 2x 4.
Решение. Преобразуем обе части уравнения, воспользовавшись тождест-
вами: sin 2x 2sin xcos x, sin2 x cos2 x 1. Последовательно имеем:
10cos2 x 5sin 2x 4;
10cos2 x 5 2sin xcosx 4(sin2 x cos2 x);
2sin2 x 5sin xcosx 3cos2 x 0.
Заметим, что среди значений x, для которых cosx 0, корней уравнения нет, поскольку, если cosx 0, то из уравнения следует, что и sin x 0, а одновременно эти два равенства выполняться не могут. Значит, можно разделить обе части уравнения на cos2 x, не опасаясь потери корней. После деления получим уравнение
2tg2 x 5tg x 3 0.
Решив его как квадратное относительно tgx, найдем: tg x 0,5, tg x 3, от-
куда x arctg0,5 n, x arctg3 n. Ответ: arctg0,5 n,arctg3 n, n Z.
симметрические уравнения
Рассмотрим тригонометрические уравнения f (x) 0, левая часть которых представляет собой рациональное выражение от переменных t sinx cosx (или t sinx cosx) и v sinxcosx. Посколь-
ку
t2 sinx cosx 2 1 2sinxcosx 1 2v,
|
v |
t2 |
1 |
|
||
то |
|
|
|
, |
если t sinx cosx, и |
|
|
|
2 |
||||
|
|
|
|
|
|
|
v |
1 t2 |
|
|
|
||
|
, |
если |
t sinx cosx. Следова- |
|||
|
||||||
|
2 |
|
|
|
|
|
тельно, исходное уравнение сводится к
алгебраическому относительно |
перемен- |
|||||||
ной |
t. |
|
Так |
как |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sinx cosx |
|
2sin |
x |
|
|
, то |
поиск |
|
|
|
|||||||
|
|
|
|
|
4 |
|
|
|
корней алгебраического уравнения мож-
но ограничить промежутком t 
 2 .
2 .
Пример 45. Решить уравнение
1 2sin xcosx 2 sin x cosx 0.
Решение. Введем новую переменную
sin x cosx t, |
|
t |
|
|
|
2 . С учетом равен- |
||||||||||||||||
ства |
sin xcosx |
|
t |
2 1 |
перепишем |
урав- |
||||||||||||||||
|
|
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 1 |
|
|
|
|
||
нение в виде |
1 2 |
|
|
2t |
0, |
или |
||||||||||||||||
|
2 |
|||||||||||||||||||||
t t 2 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Последнее |
уравнение имеет |
||||||||||||||||||||
два корня |
|
t1 0 |
и |
t2 |
2, из которых |
|||||||||||||||||
только первый |
удовлетворяет |
|
|
условию |
||||||||||||||||||
|
t |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
x. Полу- |
||||
|
|
|
|
|
|
Вернемся к переменной |
|
|||||||||||||||
чим |
|
|
|
|
sin x cosx 0, |
|
|
|
или |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2sin x |
|
0, |
откуда x |
|
|
n. |
||||||||||||||
|
|
|
4 |
|||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: n, n Z. 4
Пример 46. Решить уравнение
sin3 x cos3 x sin xcosx 1.
Решение. Воспользовавшись формулой разности кубов
sin3 x cos3 x (sin x cosx)
(sin2 x sin xcosx cos2 x)
25.12.2011 www.alexlarin.net |
24 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
перепишем уравнение в виде
(sin x cosx)(1 sin xcosx) sin xcosx 1.
|
|
|
|
Положим sin x cosx t , |
t |
|
2 . То- |
||||||||||||||||||||||||||||
гда |
t2 sinx cosx 2 |
1 2sinxcosx, и, |
|||||||||||||||||||||||||||||||||
значит, sin xcosx |
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
. Таким образом, |
||||||||||||||||||||||||||||
|
|
|
2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
после замены получим уравнение |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t |
2 |
1 t |
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
1 0, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
которое преобразуется к виду |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
1 t |
|
|
(t 1) 0, или 3 t2 (t 1) 0. |
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда |
|
|
|
t1,2 |
|
|
|
, |
|
|
t3 |
1. |
Условию |
||||||||||||||||||||||
|
|
|
3 |
|
|
||||||||||||||||||||||||||||||
|
t |
|
|
|
|
|
|
удовлетворяет только |
|
одно из |
|||||||||||||||||||||||||
|
|
2 |
|
|
|||||||||||||||||||||||||||||||
найденных значений: t |
1. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
Возвратимся к исходной переменной. |
|||||||||||||||||||||||||||||||
Получим |
|
|
|
|
sin x cosx 1, |
|
|
|
или |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2sin x |
|
|
1, sin |
x |
|
|
|
|
|
|
|
|
, отку- |
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||
да |
|
|
|
|
|
|
x |
|
|
|
2 n |
|
|
|
или |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x 2 n . Таким образом, ис- 4 4
ходное уравнение имеет две серии реше-
ний: x 2 n и x 2 n. 2
Ответ: 2 n, 2 n, n Z. 2
Уравнения f (x) 0, левая часть которых может быть представлена как многочлен от tgx ctgx, сводятся к алгебраическим заменой tgx ctgx t .
Пример 47. Решить уравнение
tg2 x ctg2 x 3 tgx ctgx 4 0.
Решение. Положим tgx ctgx t . Заметим, что
tgx ctgx |
1 |
|
2 |
|
|||
|
sinxcosx |
sin2x |
|||||
|
|
|
|||||
и, следовательно, |
|
t |
|
2. Поскольку |
|||
|
|
||||||
tg2 x ctg2 x
(tgx ctgx)2 2tgx ctgx t2 2,
то после замены получим уравнение
t2 2 3t 4 0, или t2 3t 2 0.
Последнее уравнение имеет |
два |
корня |
||||||||
t 1 и t 2, |
из которых только второй |
|||||||||
удовлетворяет |
условию |
|
t |
|
|
2. |
Если |
|||
|
|
|||||||||
t 2, то tgx ctgx 2, |
или |
sin 2x 1, |
||||||||
откуда x |
|
n, n Z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
n, n Z . |
|||||
|
|
|
4 |
|||||||
|
|
|
|
|
|
|
|
|
||
применение универсальной тригонометрической подстановки
Так как sinx, cosx, tgx |
и ctgx |
выра- |
|||||
жаются |
через tg |
x |
, то уравнение |
вида |
|||
|
|||||||
|
|
|
2 |
|
|
|
|
f (sin x,cosx,tgx,ctgx) 0 |
подстановкой |
||||||
t tg |
x |
|
часто удается свести к алгебраи- |
||||
|
|||||||
2 |
|
|
|
|
|
|
|
ческому уравнению. При этом следует
иметь |
в |
виду, |
что замена |
sin x на |
|||||||||
|
2tg |
x |
|
|
|
|
1 tg2 |
x |
|
||||
|
|
|
|
|
|
2 |
|
|
|
||||
|
2 |
|
|
|
и cosx |
на |
|
|
|
ведет к су- |
|||
|
x |
|
|
|
|||||||||
1 tg2 |
|
|
1 tg2 |
x |
|
||||||||
|
2 |
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
жению области определения уравнения, поскольку из рассмотрения исключаются
значения x, |
при которых |
cos |
x |
0, т.е. |
|
||||
|
|
2 |
|
|
x 2 n. |
Поэтому при |
применении |
||
универсальной тригонометрической подстановки необходимо дополнительно выяснить, являются или нет исключаемые из рассмотрения значения x корнями исходного уравнения.
Пример 48. Решить уравнение
tgx 1 2sin 1,5 2x .
Решение. |
Преобразовав уравнение к |
|
виду tgx 1 2cos2x, |
введем новую |
|
переменную |
tgx t . Так |
как исходное |
уравнение не определено для x n, 2
то такая замена не может привести к по-
25.12.2011 www.alexlarin.net |
25 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
тере корней. Заменив cos2x на |
1 t2 |
, |
|||
|
|
||||
1 t2 |
|||||
1 t2 |
|
||||
|
|
|
|||
получим уравнение t 1 2 |
|
, кото- |
|||
|
|||||
1 t2 |
|
|
|
||
рое равносильно каждому следующему уравнению:
(t 1)(1 t2 ) 2(1 t2 ) 0; (t 1)(1 t2 ) 2(1 t)(1 t) 0; (t 1)(t2 2t 3) 0.
Получаем t 1 и, возвращаясь к переменной x, решаем уравнение tg x 1.
Отсюда x n, n Z. 4
Ответ: n, n Z. 4
Тренировочные упражнения
Решите уравнение:
29. 2sin2 x 19sin x 10 0. 2 2
30. 2cos2 x 5sin x 1 0.
31.2(sin x cosx) sin2x 0,56.
32.5sin 2x 11(sin x cosx) 7 0.
33. 3sin2 x 4sin xcosx 5cos2 x 2.
34. 5sin2 x 2sin xcosx cos2 |
x 4. |
||||||||||||||||||||||||
35. 3tgx 2ctgx 5. |
|
|
|
|
|
|
|
||||||||||||||||||
36. 4tgx 3ctgx 1. |
|
|
|
|
|
|
|
||||||||||||||||||
|
4cos |
2 x |
|
|
|
|
|
|
x |
sin |
x |
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
sin |
2 |
|
|
|
|
|
||||||||||||
37. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
sin x |
2 |
|
|
|
|
. |
|
||||||||||||||
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|||||||||
|
cos |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
38. 3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
x |
|
|
|
||||
39. Решите уравнение |
|
|
|
|
|
|
|||||||||||||||||||
6cos2 x 7cosx 5 0.
Укажите корни, принадлежащие отрезку
[ ;2 ].
40. Решите уравнение
4sin2 x 12sin x 5 0.
Укажите корни, принадлежащие отрезку
[ ;2 ].
41. Дано уравнение
2sin2 x 3cosx 3 0.
25.12.2011 www.alexlarin.net |
26 |
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку [ ;3 ].
42. Дано уравнение
sin2 x 2sin x cosx 3cos2 x 0.
а) Решите уравнение.
б) Укажите корни, принадлежащие от-
|
|
|
||
резку |
; |
|
. |
|
2 |
||||
|
|
|
||
43. Дано уравнение tg2 x 5tgx 6 0. а) Решите уравнение.
б) Укажите корни, принадлежащие от-
|
|
|
|
|
||
резку |
2 ; |
|
. |
|
|
|
|
|
|
||||
|
|
2 |
|
|
||
44. Дано уравнение |
1 |
|
4tgx 6 0. |
|||
cos2 |
|
|||||
|
|
|
|
x |
||
а) Решите уравнение.
б) Укажите корни, принадлежащие от-
|
|
7 |
|
|
|
||
резку |
2 ; |
|
. |
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
||
45. Дано уравнение |
1 |
|
2 |
3 0. |
|||
tg2 x |
|
||||||
|
|
|
|
|
tgx |
||
а) Решите уравнение.
б) Укажите корни, принадлежащие от-
|
|
7 |
||
резку |
2 ; |
|
. |
|
2 |
||||
|
|
|
||
2.3. Метод разложения на множители
Один из основных подходов к решению тригонометрических уравнений состоит в их последовательном упрощении с целью сведения к одному или нескольким простейшим. Для упрощения используются тригонометрические формулы. Универсального ответа на вопрос, какие формулы следует применить в том или ином случае, нет, однако есть ряд приемов, которые полезно иметь в виду при поиске решения.
Довольно часто в результате преобразований удается привести уравнение к виду f1(x) f2 (x) ... fk (x) 0. В этом случае дальнейшее решение сводится к поиску корней уравнений f1(x) 0, f2 (x) 0, …, fk (x) 0 и дальнейшему
отбору тех из них, которые принадлежат области определения исходного уравнения.
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Такой подход к решению уравнений, известный как метод разложения на множители, является универсальным (его применяют при решении рациональных, иррациональных, показательных и логарифмических уравнений).
Пример 49. Решить уравнение
6sin xcosx sin 2xsin 2 0. x
Решение. Воспользуемся формулой синуса двойного аргумента
|
3sin 2x sin 2xsin |
2 |
0, |
|||||||
|
|
|||||||||
|
|
|
|
2 |
|
x |
||||
|
|
|
|
|
||||||
|
sin 2x 3 sin |
|
|
|
0. |
|||||
|
|
|
||||||||
|
|
|
|
x |
|
|
||||
Так |
как 3 sin |
2 |
|
0, |
|
то последнее |
||||
x |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
уравнение равносильно системе |
||||||||||
sin 2x 0 |
|
k |
|
|
|
|||||
|
x |
|
|
|
|
, |
k Z, k 0. |
|||
2 |
|
|||||||||
x 0, |
|
|
|
|
||||||
Ответ: k , k Z, k 0. 2
Пример 50. Решить уравнение
tgx(sin x 1) 0.
Решение. Так как общий наименьший период функций tgx и sin x равен 2 , то отбор корней удобно проводить на промежутке [0;2 ). Проведем равносильные преобразования:
|
|
|
|
|
|
|
sin x 0, |
|
||
tgx(sin x 1) |
0 |
|
|
|
||||||
sin x 1, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosx 0 |
|
||
|
x n, |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
x |
2 k, |
n, k, l Z. |
|||||||
|
|
|||||||||
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
x |
m, |
|
|
|
|||||
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
На промежутке [0;2 ) из трех корней
0, |
|
, |
исключаем число |
|
, поэтому |
|
2 |
||||
2 |
|
|
|
||
множество корней данного уравнения задается формулой x l, l Z.
25.12.2011 www.alexlarin.net
Ответ: l, l Z.
Пример 51. Решить уравнение
cos8x tgx tgx.
Решение. Перепишем уравнение в ви-
де
tgx cos8x 1 0.
Функции, входящие в последнее уравнение, определены при всех x кроме
x |
|
n, |
n Z . На этом множестве |
|
|||
2 |
|
|
|
последнее уравнение равносильно совокупности уравнений tgx 0 и cos8x 1, решения которых определяются форму-
лами x n и x n , n Z . 4
Теперь необходимо отобрать из полу-
ченных значений x те, |
которые удовле- |
|||||||||||||||
творяют |
|
условию |
|
|
cosx 0, |
т.е. |
||||||||||
x |
|
n, |
n Z . Для первой серии кор- |
|||||||||||||
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ней условие cosx 0 |
|
выполняется. |
Для |
|||||||||||||
отбора корней второй серии |
x |
n |
|
вос- |
||||||||||||
|
||||||||||||||||
пользуемся следующим. |
|
4 |
|
|
||||||||||||
n |
|
|
|
|
|
|||||||||||
|
Представим |
число |
в |
виде |
||||||||||||
n 4k p , |
где |
k Z , |
а p |
принимает |
||||||||||||
значения 0, 1, 2 и 3. Тогда при разных |
||||||||||||||||
значениях |
p корни второй серии будут |
|||||||||||||||
иметь вид: |
|
|
|
|
|
|
|
|
|
|
||||||
x k |
при p 0; x |
k |
при p 1; |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
||
x |
k |
при |
p 2 |
и |
x |
k при |
||||||||||
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||
p 3.
Значит при p 2 получаются «запрещенные» значения, а все оставшиеся решения можно задать, например, как сово-
купность серий: |
|
|
n |
и n, |
n Z, |
|
2 |
||||
4 |
|
|
|
||
причем вторая из этих серий была получена ранее.
Ответ: n , n, n Z. 4 2
В случае тригонометрических уравнений проблема преобразования исходного
уравнения к виду уравнения к |
виду |
f1(x) f2 (x) ... fk (x) 0 решается, |
глав- |
27
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
ным образом, путем использования тригонометрических формул. Рассмотрим, как это делается, на примерах.
Пример 52. Решить уравнение
cos2x sin x cosx 0.
Решение. Так как
cos2x cos2 x sin2 x,
то данное уравнение равносильно следующим:
cosx sin x cosx sin x cosx sin x 0;
cosx sin x cosx sin x 1 0.
Полученное уравнение в свою очередь равносильно совокупности уравнений
cosx sin x 0 и cosx sin x 1 0.
|
|
|
|
|
|
|
|
|
|||
1) cosx sin x 0; |
2cos x |
|
|
0; |
|
|
|||||
|
|
|
4 |
|
|
x n; x n, n Z .
4 |
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
2) cosx sin x 1 0; |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
||||||||||
2cos x |
|
|
1; |
cos x |
|
|
|
|
|
|
; |
||
|
|
|
|
|
|||||||||
|
|
2 |
|||||||||||
|
|
|
4 |
|
|
4 |
|
|
|
||||
x 3 2 n, n Z . 4 4
Ответ: n, 3 2 n, n Z .
4 |
4 |
4 |
Если уравнение содержит выражения sin sin , cos cos , то для разло-
жения на множители можно попробовать применить формулы преобразования этих сумм (разностей) в произведения.
Пример 53. Решить уравнение
sin x sin 2x sin3x sin 4x 0.
Решение. Перепишем уравнение в ви-
де sin x sin3x sin 2x sin 4x 0. Да-
лее преобразуем это уравнение, используя формулу
sin sin 2sin cos . 2 2
Получим
2sin 2xcosx 2sin3xcosx 0; cosx sin 2x sin3x 0;
cosx sin 5x cos x 0. 2 2
Последнее уравнение распадается на три:
1)cosx 0; x n; 2
2)sin 5x 0; x 2 n , n Z ;
25
3)cos x 0; x 2 n, n Z . 2
Ответ: n, 2 n , 2 n, n Z . 2 5
Пример 54. Найти наибольший отрицательный корень уравнения
sin x sin 2x sin3x 0 .
Решение. Последовательно имеем
|
sin x sin 2x sin3x 0 |
|
|
|
|
|||||||||||||||||||||||||||||
|
2sin |
3x |
|
cos |
x |
|
sin3x 0 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2sin |
3x |
cos |
x |
|
2sin |
3x |
cos |
3x |
|
0 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
3x |
|
|
|
|
|
|
x |
|
|
|
|
3x |
|
|
|
|
|
|
|
|
||||||||||
2sin |
|
cos |
|
|
|
cos |
|
|
0 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
0, |
|||
|
3x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
sin |
cos |
cosx 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||||||||
2 |
2 |
|
|
cos |
0, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosx 0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n, k, l Z. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x 2 k, |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
l, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Продемонстрируем применение различных способов для отбора наибольшего отрицательного корня данного уравнения.
Алгебраический способ. Для каждой серии корней решим неравенства относительно соответствующего параметра n, k и l.
а) Для первой серии корней имеем
2 n |
0, n Z . Отсюда получаем |
n 0, |
|
3 |
|||
|
|
а наибольшее целое отрицательное зна-
чение n 1 и корень x 2 . 3
25.12.2011 www.alexlarin.net |
28 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
б) Второе неравенство 2 k 0, k Z, выполняется, если k 0,5; k Z, или k 1 и x .
в) x |
|
l, l Z, и |
|
l 0, тогда |
2 |
|
2 |
|
|
l 1, l Z, или l 1 и x .
2 |
2 |
Выбираем наибольший отрицательный
корень уравнения x . 2
Арифметический способ. Выполнив перебор значений параметров n, k и l, найдем значения для переменной х.
а) |
x |
2 n |
, n Z . |
Пусть |
n 0, тогда |
||||||||||||||
|
|
|
|||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
x 0. Если n 1, то x |
. |
|
|
||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
б) |
x 2 k, k Z. Последовательно |
||||||||||||||||||
подставляем |
k 0 |
и |
|
k 1, получаем |
|||||||||||||||
x и x соответственно. |
|||||||||||||||||||
в) |
x |
|
l, l Z. Тогда при l 0 и |
||||||||||||||||
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
l 1 вычисляем |
x |
и |
x |
. Так |
|||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
||||||
как |
|
|
, |
то наибольший от- |
|||||||||||||||
|
|
||||||||||||||||||
|
3 |
2 |
|
|
|
|
|
|
|
|
|
||||||||
рицательный корень уравнения x . 2
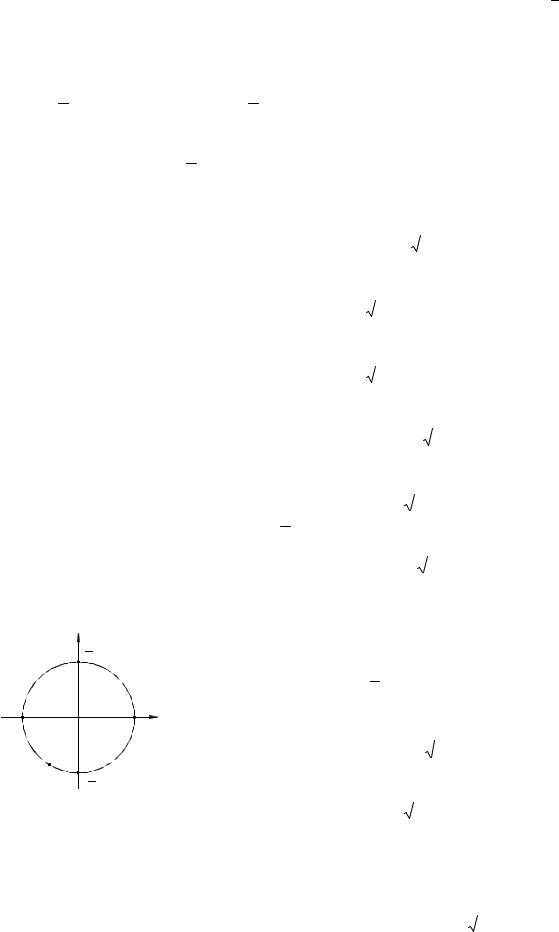
Геометрический способ. На тригоно-
метрическом круге изобразим точками числа, соответствующие найденным сериям решений (рис. 22).
|
|
y |
|
При обходе по |
||||
|
|
|
тригонометриче- |
|||||
|
|
|
|
|||||
|
|
|
|
ской окружности в |
||||
|
|
|
|
отрицательном |
||||
|
|
O |
|
направлении пер- |
||||
|
|
x вое встретившееся |
||||||
|
|
|
||||||
|
|
|
|
число есть |
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
. |
||||
|
|
Рис. 22 |
||||||
|
|
|
||||||
|
|
2 |
|
|||||
Тренировочные упражнения
46. Найдите все решения уравнения sin 2x cosx, принадлежащие промежут-
|
|
3 |
|
|
ку |
; |
|
. |
|
|
|
|||
|
|
4 |
|
|
25.12.2011 www.alexlarin.net |
29 |
|||
47. Найдите все корни уравнения
(2sin x 1)(2sin x 
 3) 0,
3) 0,
удовлетворяющие неравенству cosx 0.
48. Решите уравнение
cos12x sin4x 0.
49. Решите уравнение
|
|
|
|
|
|
|
|
|
|
|
|
cosxcos5x 0. |
|
|||
50. |
Найдите сумму корней уравнения |
|||||||||||||||
(tgx 1)(sin x 1) 0, |
принадлежащие |
|||||||||||||||
промежутку [ 50 ; 350 ]. |
|
|
||||||||||||||
51. |
Найдите сумму корней уравнения |
|||||||||||||||
(ctgx |
|
|
|
|
|
|
|
принадлежащие |
||||||||
3)sin2x 0, |
||||||||||||||||
промежутку [ 100 ; 300 ]. |
|
|
||||||||||||||
52. |
Найдите |
все |
корни |
уравнения |
||||||||||||
( |
|
|
sin x 1)(2sin x 3) |
0, |
удовлетво- |
|||||||||||
2 |
|
|||||||||||||||
ряющие неравенству tgx 0. |
|
|||||||||||||||
53. |
Найдите |
все |
корни |
уравнения |
||||||||||||
( |
|
cosx 1)(2cosx 1) 0, |
удовлетво- |
|||||||||||||
2 |
||||||||||||||||
ряющие неравенству sinx 0. |
|
|||||||||||||||
54. |
Найдите |
все |
корни |
уравнения |
||||||||||||
(2cosx |
|
|
|
|
|
|
3)(3cosx 4) 0, |
удовлетво- |
||||||||
|
|
|
|
|
|
|||||||||||
ряющие неравенству tgx 0. |
|
|||||||||||||||
55. |
Найдите |
все |
корни |
уравнения |
||||||||||||
(tgx |
|
|
3)(2cosx 1) 0, |
удовлетворяю- |
||||||||||||
|
|
|||||||||||||||
щие неравенству sinx 0 . |
|
|
||||||||||||||
56. |
Найдите |
все |
корни |
уравнения |
||||||||||||
(tgx 1)( |
|
|
|
sin x 1) 0, |
удовлетворяю- |
|||||||||||
|
|
2 |
||||||||||||||
щие неравенству cosx 0. |
|
|
||||||||||||||
57. |
Найдите |
все |
корни |
уравнения |
||||||||||||
3tg2 x 1, удовлетворяющие неравенству
sinx 0.
58. Найдите все корни уравнения

 2sin2 x sin x, удовлетворяющие неравенству cosx 0.
2sin2 x sin x, удовлетворяющие неравенству cosx 0.
59. |
Найдите |
|
все |
корни |
уравнения |
||||||||||
2cos2 x |
|
|
cosx 0, |
удовлетворяющие |
|||||||||||
3 |
|||||||||||||||
неравенству sin x 0. |
|
|
|
|
|||||||||||
60. |
Найдите |
|
все |
корни |
уравнения |
||||||||||
tg2x |
|
3 |
tgx, |
|
удовлетворяющие нера- |
||||||||||
венству cosx 0. |
|
|
|
|
|||||||||||
61. |
Решите уравнение ctgx cosx 0. |
||||||||||||||
62. Решите уравнение tgx sin x 0. |
|||||||||||||||
63. |
Решите уравнение |
|
|
||||||||||||
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|||||||||
|
ctg |
|
|
|
|
3 cos |
|
1 |
0. |
||||||
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
4 |
|
|
|||||

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
64. Решите уравнение
sin x sin5x cos4x.
65. Решите уравнение
cosx cos5x cos6x .
66. Укажите все корни уравнение
sin 2x |
2sin x 0, |
|
|
||||
|
|
|
3 |
3 |
|||
принадлежащие отрезку |
|
|
; |
|
. |
||
2 |
2 |
||||||
|
|
|
|
|
|||
67. Решите уравнение
(x2 5x 6) arcsin x 0. 2
68. Решите уравнение
(x 2)(2x2 7x 3) arccos x 0. 2
69. Дано уравнение
2sin 2x 4cosx sin x 1.
а) Решите уравнение.
б) Укажите корни, принадлежащие отрез-
3
ку ; .
2 2
70. Дано уравнение
3sin 2x 4cosx 3sin x 2 0.
а) Решите уравнение.
б) Укажите корни, принадлежащие отрез-
3
ку ; .
2 2
71. Дано уравнение
sin 2x 2sin x cosx 1.
а) Решите уравнение.
б) Укажите корни, принадлежащие отрез-
|
|
|
||
ку |
2 ; |
|
. |
|
2 |
||||
|
|
|
||
72. Дано уравнение
sin8xcos2x sin 7xcos3x.
а) Решите уравнение.
б) Укажите корни, принадлежащие отрез-
|
|
|
||
ку |
|
|
; . |
|
2 |
||||
|
|
|
||
73. Дано уравнение
sin10xsin 2x sin8xsin 4x.
а) Решите уравнение.
б) Укажите корни, принадлежащие отрез-
|
|
|
|
|||
ку |
|
|
; |
|
. |
|
6 |
2 |
|||||
|
|
|
|
|||
2.4. Функциональный метод
Область применения свойств функции при решении уравнений очень широка. Наличие свойств (ограниченность, монотонность и т.д.) функций, входящих уравнение позволяет применить нестандартные методы решения к стандартным по формулировке задачам – уравнениям.
Использование области определения функций
Предварительный анализ области допустимых значений неизвестной уравнения иногда позволяет получить корни без преобразований уравнения.
Рассмотрим ограничения, связанные с областью определения и множеством значений функции.
Пример 55. Решить уравнение
arccos3x 4 x 6 . 1 2x
Решение. В соответствии с определением арккосинуса запишем ограничения, которым должен удовлетворять x. Область допустимых значений уравнения
определяется условиями 1 3x 4 1, а 1 2x
поскольку значения арккосинуса ограничены отрезком 0, , то для выполнения равенства необходимо выполнение усло-
вия 0 x 6 . |
Получаем систему |
||||||||||||
неравенств |
|
|
|
|
|
|
|
|
|
||||
|
3x 4 |
|
|
|
|
|
3x 4 |
1, |
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
1, |
|
|
1 2x |
|
||||
1 2x |
|
||||||||||||
|
|
|
|
3x 4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1, |
||
|
|
|
|
|
|
|
|
|
|||||
0 x 6 |
|
|
1 2x |
|
|||||||||
|
|
|
|
|
|
|
|
|
0 x 6 1 |
||||
|
|
x 5 |
0, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 2x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x 5. |
||||||
5x 3 |
|
||||||||||||
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 2x |
|
|
|
|
|
|
|
||||
|
|
6 x 5 |
|
||||||||||
Подставляя полученное единственное значение x 5 в исходное уравнение, получим
arccos3 ( 5) 4 ( 5) 6 , 1 2 ( 5)
25.12.2011 www.alexlarin.net |
30 |
