
C1 2012 корянов
.pdf
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Ответ: t, t Z.
1.2. Алгебраический способ
Алгебраический способ отбора корней наиболее удобен в тех случаях, когда последовательный перебор значений параметров приводит к вычислительным трудностям, промежуток для отбора корней большой, значения обратных тригонометрических функций, входящих в серии решений, не являются табличными, и при решении задач с дополнительными условиями.
решение неравенства относительно неизвестного целочисленного параметра и вычисление корней
Пример 16. Найти все решения сово-
купности уравнений |
cosx 0 |
, принад- |
|||
|
|
|
|||
|
sin x 0,5 |
||||
|
|
|
3 |
||
лежащие промежутку |
; |
|
. |
||
4 |
|||||
|
|
|
|
||
Решение. |
1. |
|
|
cosx 0, |
|
x n; n Z. Так как решения долж-
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ны |
удовлетворять |
|
неравенству |
||||||||||||
|
|
n |
3 |
, то, сократив на |
, |
по- |
|||||||||
|
|
||||||||||||||
2 |
|
1 |
4 |
|
3 |
|
|
3 |
|
|
1 |
|
|||
лучим |
1 |
n |
или |
|
n |
. С |
|||||||||
|
|
|
|
||||||||||||
|
|
2 |
4 |
|
2 |
|
4 |
|
|||||||
учетом того, что n Z , получаем два значения n 1 и n 0. Если n 0, то
x |
|
, если n 1, то |
x |
|
. |
|
|||
|
|
|
|||||||
2 |
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 n, |
|
|||
|
|
6 |
|
|
|||||
2. sin x 0,5 |
|
|
|
|
|
n Z . |
|||
5 |
|
|
|
||||||
|
|
|
|
|
|
|
|||
|
|
x |
|
|
|
2 n, |
|
||
|
|
6 |
|
|
|||||
|
|
|
|
|
|
|
|
||
Так как должно выполняться условие
x 3 , то для первой серии имеем
4
2 n 3 1 1 2n 3 6 4 6 4
7 n 7 n 0. 12 24
Отсюда получаем x . 6
25.12.2011 www.alexlarin.net
Для второй серии имеем
5 2 n 3 1 5 2n 3 6 4 6 4
11 n 1 . 12 24
Последнее неравенство не имеет целочисленных решений.
Ответ: |
|
; |
|
; |
|
. |
2 |
|
2 |
|
6 |
|
|
Пример 17. Найти все решения сово-
cos5x 0,
купности уравнений принад-
cosx 0,
лежащие отрезку [1;2].
Решение. Найдем решения совокупности уравнений
|
|
|
|
|
|
k |
|
|
cos5x 0 |
x |
|
|
|
|
|
|
, |
|
|
|
|
|
||||
|
|
10 5 k, n Z. |
||||||
cosx 0 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
n, |
|
||
|
2 |
|
|
|||||
|
|
|
|
|
|
|
||
Заметим, что первую серию решений
можно записать в виде x (1 2k) , а 10
вторую – x (1 2n) . Отсюда можно
2
заметить, что решения второй серии содержатся в первой, так как их можно записать в виде
x |
(1 2n) |
|
(5 10n) |
|
(1 2(5n 2)) |
. |
|
10 |
10 |
||||
2 |
|
|
|
|||
Поэтому первая серия решений совокупности содержит все корни исходной совокупности уравнений. Можем записать
x |
|
|
k |
, |
k Z. Решим двойное не- |
|
|
||||
10 |
5 |
|
|
||
равенство
1 k 2 10 2 k 20
105
10 2 k 20
|
10 |
|
k |
20 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
5 |
|
1 |
|
k |
10 |
|
1 |
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
||||||||||||||
Так как |
5 |
|
1 |
|
|
5 |
|
1 |
|
17 |
, |
10 |
|
1 |
|
|||||||||||
|
2 |
|
|
|
|
3,2 |
2 |
16 |
|
|
2 |
|||||||||||||||
11

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
|
10 |
|
1 |
|
|
17 |
|
и |
k Z, то |
k 2. Тогда |
||||
|
|
2 |
|
|
||||||||||
3 |
|
|
|
2 |
6 |
|
|
|
|
|
||||
x |
|
|
|
. |
|
|
||||||||
|
|
|
|
|
||||||||||
10 |
|
5 |
|
2 |
|
|
|
|||||||
Ответ: . 2
исследование уравнения с двумя целочисленными параметрами
Пример 18. Решить систему уравнений:
cos2x 1,
|
|
|
|
|
5x |
|
|
|
|
|
|
|
|
sin |
|
|
1. |
|
|
||
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Решение. Получаем решения системы |
||||||||||
cos2x 1, |
|
x n, |
|
|
||||||
|
5x |
|
|
|
|
|
|
|
4 m |
n, m Z. |
|
|
|
|
|
|
|||||
sin |
|
1 |
|
x |
|
|
|
, |
||
2 |
|
5 |
5 |
|||||||
|
|
|
|
|
|
|
|
|||
Найдем такие целые значения n и m, при которых решения в полученных сериях совпадают, т.е. приравнивая выражения для x в обеих сериях, получим
n |
|
|
4 m |
или |
5n 1 4m. |
||||
|
|
||||||||
5 |
|
5 |
|
|
|
|
|
|
|
Далее получим |
|
|
|
|
|||||
4m 5n 1 |
или m |
5n 1 |
n |
n 1 |
. |
||||
|
|
||||||||
|
|
|
|
|
|
4 |
4 |
|
|
Для существования целых решений число
n 1 должно быть целым. Обозначим его
4
буквой k , тогда
|
n 1 |
k |
или n 4k 1, где k Z. |
|||||
4 |
||||||||
|
|
|
|
|
|
|||
Тогда m |
5n 1 |
|
20k 4 |
5k 1, k Z. |
||||
|
4 |
|||||||
|
|
|
|
4 |
|
|
||
Подставляя n 4k 1, k Z, в первую серию решений или m 5k 1, k Z, во вторую, получим общее решение
x (4k 1), |
k Z. |
|
|
Ответ: (4k 1), |
k Z . |
Пример 19. Решить систему уравнений:
sin11x 1,
sin3x 1.
Решение. Найдем решения системы
|
|
|
|
|
|
2 n |
|||
sin11x 1, |
x |
|
|
|
|
|
|
, n Z, |
|
22 |
11 |
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
2 m |
|
|
||
sin3x 1. |
|
|
|
|
|
||||
|
x |
6 |
|
|
|
3 |
, m Z. |
||
|
|
|
|
|
|
|
|
||
Найдем такие целые значения n и m, при которых решения в полученных се-
риях совпадают |
|
|
2 n |
|
|
|
2 m |
, |
|
|
6 |
|
|||||
22 |
11 |
|
3 |
|
||||
т.е. 3n 2 11m. Выражая из последнего
равенства n, получаем n 3m 2m 2 . 3
Так как n – целое, то последнее равенство возможно, только если число 2m 2 делится на 3, т.е. 2m 2 3k , k Z. От-
сюда m 1 k k . Поскольку m должно
|
|
2 |
|
|
|
|
|
|
|
|||
быть целым, то k |
должно быть четным. |
|||||||||||
Если |
k 2p, |
где |
p Z, |
то |
||||||||
m 1 2p |
2p |
|
3p 1. |
Следователь- |
||||||||
|
||||||||||||
но, |
2 |
|
|
|
|
|
|
|
|
|||
|
2 (3p 1) |
|
|
|
|
|
|
|||||
x |
|
|
|
|
2 p , p Z. |
|||||||
|
|
|
||||||||||
6 |
3 |
2 |
|
|
|
|
||||||
|
|
|
|
|
Ответ: |
2 p , |
p Z. |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
||||
Пример 20. Решить систему:
cos7x 0,
cos2x 0,
sin5x 0.
Решение. Из системы имеем
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
x |
|
|
|
|
|
|
|
, |
n Z, |
|||
cos7x 0, |
|
14 |
7 |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
||
cos2x 0, |
|
x |
|
|
|
|
|
|
|
, |
|
k Z, |
||
4 |
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin5x 0 |
|
|
|
m |
|
|
|
|
|
|
||||
|
|
x |
|
|
|
|
|
|
, |
|
|
|
m Z. |
|
|
|
5 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
25.12.2011 www.alexlarin.net |
12 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
Выясним, какие из значений
x n , n Z , являются недопусти14 7
мыми. Для этого решим в целых числах уравнения
(а) |
|
|
n |
|
|
|
k |
и (б) |
|
|
|
n |
|
m |
. |
14 |
7 |
4 |
2 |
|
14 |
7 |
5 |
|
|||||||
Рассмотрим уравнение (а). После преобразований получим:
2 4n 7 14k 4n 14k 5.
Последнее равенство невозможно, так как в левой его части получаются при всех значениях n и k четные числа, а в правой – число нечетное.
Рассмотрим уравнение (б). После преобразований получим:
5 10n 14m 14m 10n 5.
Последнее равенство невозможно, т.к. в левой его части стоят четные числа, а в правой – нечетное.
Значит, все |
значения |
x |
|
|
|
n |
, |
||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
14 |
7 |
|
||||
n Z , являются допустимыми. |
|
|
|
||||||||||
|
Ответ: |
|
|
n |
, |
n Z. |
|||||||
|
14 |
|
|||||||||||
|
|
|
|
|
|
7 |
|
|
|
|
|
||
Пример 21. Найти сумму решений си- |
|||||||||||||
стемы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
||||
cos |
|
|
|
0, |
|
|
|
||||||
4 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x 2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
sin |
|
|
|
|
0, |
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
принадлежащих промежутку [ ;80 ].
Решение. Получаем из системы
|
x 3 |
|
|
x 3 |
|
|
|
|||||
cos |
|
|
|
0, |
|
|
|
|
|
n, |
||
4 |
|
|
|
|
||||||||
|
|
4 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||||
|
x 2 |
|
x 2 |
|
|
|
||||||
|
|
|
|
k, |
||||||||
sin |
|
|
|
|
0 |
|
|
3 |
||||
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
n,k Z, x 4 n, n Z, |
|||||||||||
|
|
|
|
|
|
x 2 3 k, k Z. |
||||||
На отрезке [ ;80 ] |
значения |
x 4 n, |
||||||||||
n Z , образуют арифметическую прогрессию с разностью 4 и первым членом 3 .
Количество членов этой прогрессии можно найти из неравенства:
4 n 80 , n Z
0,5 n 20,25, n Z.
Таким образом, n может принимать все натуральные значения от 1 до 20 включительно. Значит, количество членов прогрессии N 20.
Найдем сумму S1 этих двадцати членов:
S |
2 3 19 4 |
20 820 . |
|
|
|||
1 |
2 |
|
|
|
|
|
|
Однако |
среди |
значений x 4 n, |
|
n Z , имеются |
недопустимые. Чтобы |
||
выяснить, какие это значения, решим в целых числах уравнение:
4 n 2 3 k
k 4n 3 k n 1 n . 3 3
Поскольку k и n – целые числа, то n 3t, где t Z. Таким образом, недопустимые значения переменной x получаются при n 3t. Итак, x 12 t, t Z.
На отрезке [ ;80 ] значения x 12 t, t Z, образуют арифметическую прогрессию с разностью 12 и первым членом 11 . Очевидно, что количество членов этой прогрессии N 6. Тогда их сумма
S2 2 11 5 12 6 246 . 2
Тогда искомая сумма
S S1 S2 574 .
Ответ: 574 .
1.3.Геометрический способ
Впоследние годы в учебниках используются разные модели к иллюстрации решения простейших тригонометрических уравнений или неравенств: с применением тригонометрического круга или графика простейшей тригонометрической функции. В первом случае изображение решений связано с числовой окружностью, во втором – с числовой прямой.
25.12.2011 www.alexlarin.net |
13 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
отбор корней тригонометрического уравнения на числовой окружности
Тригонометрическую окружность удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 , или в случае, когда значения обратных тригонометрических функций, входящих в серию решений, не являются табличными.
Пример 22. Найти решения совокуп-
|
cosx 0, |
|
||||||
ности уравнений: |
|
|
|
|
|
. |
|
|
|
cos5x 0. |
|
||||||
Решение. Из совокупности уравнений |
||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cosx 0, |
x |
|
|
|
k, |
|
||
2 |
|
k,n Z. |
||||||
|
|
|
|
|
n |
|||
cos5x 0, |
|
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
, |
|
10 |
5 |
||||||
|
|
|
|
|||||
Отметим, что |
функции |
cosx и cos5x, |
||||||
входящие в совокупность уравнений, имеют общий наименьший положитель-
ный период 2 . Поэтому отбор корней |
|||||
|
|
удобно проводить |
|||
|
на числовой |
ок- |
|||
|
|||||
|
|
ружности, |
при |
||
|
этом |
используя |
|||
O |
|
градусную |
меру |
||
|
|
полученных |
ре- |
||
|
|
шений |
|
|
|
x 90 k 180 |
|||||
|
|||||
|
|
||||
Рис. 11 или
x 18 n 36 .
Из рисунка 11 видим, что вторая серия решений включает в себя первую серию.
Ответ: n , n Z . 10 5
Пример 23. Определить количество
решений системы |
cos12x 1, |
на про- |
|
||
межутке [0;2 ]. |
sin3x 0 |
|
|
|
Решение. Из условия имеем
|
|
|
n |
|
|
cos12x 1, |
|
x |
|
, |
|
|
|
||||
|
|
6 n,k Z. |
|||
|
|
||||
sin3x 0, |
|
|
k |
|
|
|
|
x |
3 |
|
, |
|
|
|
|
|
|
Функции cos12x и sin3x, входящие в систему, имеют основной период, не превосходящий 2 , поэтому проведем отбор корней уравнения системы, используя
тригонометрическую |
окружность. |
Для |
||||||||
этого |
полученные |
|
|
|
|
|
|
|
||
значения |
в |
серии |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
решений |
и |
серии |
|
|
|
|
|
|
|
|
ограничений |
изо- |
|
|
|
||||||
|
|
|||||||||
бразим |
на |
триго- |
|
O |
|
|||||
нометрической ок- |
|
|
|
|
|
|
||||
ружности (см. рис. |
|
|
|
|||||||
12) и в ответ запи- |
|
|
|
|||||||
шем количество не |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
совпавших в обеих |
|
|
|
|
|
|
||||
|
|
|
|
|
Рис. 12 |
|
||||
сериях |
|
значений |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
переменной х. |
|
|
|
|
|
Ответ: 6. |
||||
|
|
|
|
|
|
|
|
|
||
Пример 24. Найти все решения сово- |
||||||||||
купности уравнений |
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
||
|
|
|
sin x |
|
, |
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
sin x |
|
, |
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
||
удовлетворяющие неравенству cosx 0.
Решение. Получаем
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
|
|
|
2 n, |
|||||
|
|
|
|
|
6 |
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||
sin x |
|
|
|
|
5 |
|
||||||||
, |
x |
2 n, |
||||||||||||
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
6 |
|
|
||||
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|||||
sin x |
|
|
x |
|
2 k, |
|||||||||
|
|
|
|
|
||||||||||
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
2 |
2 k, |
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
n,k Z. |
|
|
|
|
|
|
|
||
Изобразим |
|
полученные |
решения на |
|||||||||||
тригонометрической окружности (см.
рис. 13).
Каждому урав- |
|
|
|
|
нению |
соответст- |
|
|
|
|
|
|
||
вуют две точки на |
|
|
|
|
тригонометриче- |
|
|
|
|
ской |
окружности. |
|
O |
|
В ответ запишем |
|
|
|
|
только |
решения, |
|
|
|
|
|
|
||
расположенные на |
|
|
|
|
|
|
|
||
дуге |
окружности, |
|
|
|
|
Рис. 13 |
|
||
соответствующей |
|
|
||
|
|
|
||
25.12.2011 www.alexlarin.net |
14 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
неравенству cosx 0, |
т.е. лежащие в I и |
|||
IV четвертях. |
|
|
|
|
Следовательно, данному условию удо- |
||||
влетворяют решения |
|
|
2 k или |
|
3 |
||||
|
|
|||
2 n, n,k Z. 6
Ответ: 2 n; 2 n , n Z.
36
Вслучае маленьких значений корней можно воспользоваться приемом «укрупнения» этих значений.
Пример 25. Решить совокупность
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
sin 8x |
|
|
|
0, |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
уравнений: |
|
|
|
|
|
4 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4x |
|
|
|
|
|
||||||
|
|
|
cos |
|
|
|
|
0. |
|
|
|
||||
|
|
|
4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Основной период функции |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sin 8x |
|
|
равен |
|
|
, cos 4x |
|
|
равен |
||||||
|
4 |
|
|
||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|||
. Так как общий период этих функций
2
равен , то при умножении на 4, период
2
станет 2 .
Из условия имеем
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
||||||
|
sin 8x |
|
|
|
0, |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
|
x |
|
|
|
|
|
|
, |
||||||||
|
|
|
|
|
|
|
32 8 k,n Z, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
n |
|
|
|||||
cos |
4x |
|
|
|
|
0 |
x |
|
|
|
|
|
|
|
, |
|||||
|
|
|
8 |
|
4 |
|
||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
2 |
|
|
k,n Z. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
4x |
|
|
|
n, |
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||






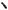
O


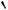











Рис. 14
Отметим на окружности полученные значения. Легко увидеть, что эти значения не совпадают (см. рис. 14).
Ответ: |
|
|
|
n |
, |
|||
|
|
|
||||||
|
|
32 |
8 |
|
||||
|
3 |
|
n |
, |
n Z. |
|||
8 |
|
|||||||
4 |
|
|
|
|
|
|||
отбор корней тригонометрического уравнения на числовой прямой
Тригонометрическую окружность удобно использовать для изображения точек вида n, n Z, где 2 : – натуральное число. Например, множеству
чисел n, n Z . на окружности со-
4 |
3 |
|
|
|
|
|
|
ответствуют |
2 : |
6 точек. С другой |
|||||
|
|||||||
|
|
3 |
|
1 |
|
||
стороны, числа вида |
3n, n Z целе- |
||||||
4 |
|||||||
|
|
|
|
|
|
||
сообразнее |
|
отмечать |
на координатной |
||||
прямой, так как число 2 не соизмеримо с числом 3, и на окружности будет бесконечное множество точек. Еще одна причина выбора числовой прямой связана с периодами функций превосходящих 2 .
Например, числа |
|
4 n, |
n Z , будут |
||
|
|||||
4 |
|
|
|
|
|
изображаться точкой P , |
но число, на- |
||||
|
4 |
|
|
||
пример, 2 , которому также соответ- 4
ствует точка P , не входит в рассматри-
4
ваемое множество чисел.
Пример 26. Решить систему:
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
cos |
|
|
|
0, |
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
sin |
|
|
|
0. |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Из условия получаем |
||||||||||
|
|
x |
|
|
|
|
|
|
||
cos |
|
|
|
0, |
|
x 2 k, |
||||
2 |
|
|||||||||
|
|
|
||||||||
|
x |
|
|
|
|
|
|
k,n Z. |
||
sin |
0 |
|
x 3 n, |
|||||||
|
|
|||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Основной период функций, входящих в
|
x |
|
|
x |
|
||
систему: T cos |
|
|
4 , |
T sin |
|
|
6 . |
|
|
||||||
|
2 |
|
|
3 |
|
||
Общий наименьший положительный период функций равен 12 .
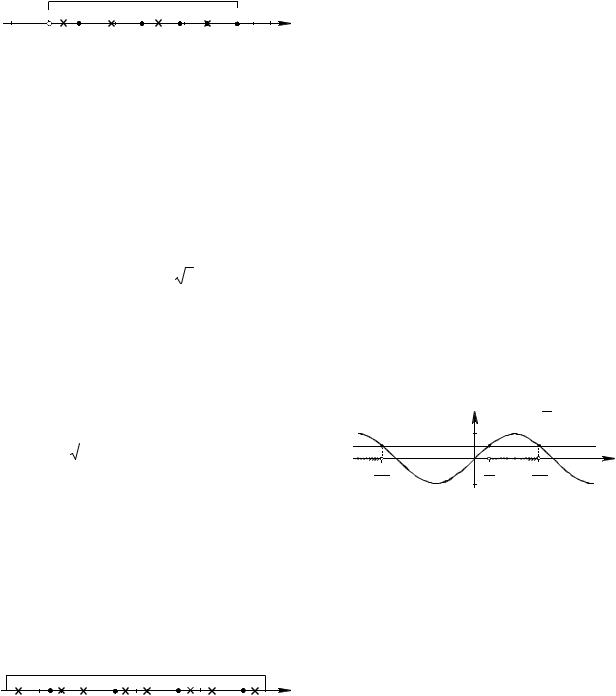
На числовой прямой (см. рис. 15) рассмотрим промежуток ( ;11 ]. Отметим черными точками числа , , 3 , 5 , 7 , 9 , 11 , соответствующие формуле
25.12.2011 www.alexlarin.net |
15 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
x 2 k, k Z. Крестиками отметим
точки 0, |
3 , 6 , |
9 , |
соответствующие |
формуле |
x 3 n, |
n Z. |
Числа, не отме- |
ченные крестиками, лучше разбить на два множества с разностью 6 и записать общий ответ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
Рис. 15
Ответ: 6 n, 5 6 n Z.
Замечание. Исходя из формул систе-
x 2 k,
мы k,n Z, достаточно бы-
x 3 n,
ло рассмотреть на числовой прямой промежуток ( ;5 ].
Пример 27. Определить количество решений системы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
sin x |
, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
на промежутке [ 3;5]. |
|
|
|
|
|
|
|
||||||||||||||||||
|
Решение. Из условия имеем |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2k, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||
sin x |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
k,n Z, |
||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
2k, |
||||||||||||
|
|
|
|
1 |
|
3 |
|
||||||||||||||||||
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
2n, |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
2k, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k, n Z. |
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
3 |
|
2n, |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||
Рис. 16
Полученные значения в серии решений и серии ограничений изобразим на координатной прямой в промежутке [ 3;5] и в ответ запишем количество не
совпавших в обеих сериях значений переменной x (см. рис. 16).
Ответ: 4.
1.4. Функционально-графический способ
При изображении решений простейших тригонометрических неравенств иногда используют графики простейших тригонометрических функций. Для нахождения решения тригонометрического неравенства при этом подходе требуется схематичное построение графика простейшей тригонометрической функции и применение формул корней соответствующих уравнений.
Пример 28. Решить неравенства:
а) sin x |
1 |
; |
|
|
б) sin x |
1 |
. |
|||||||
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
||
Решение. Схематично изобразим гра- |
||||||||||||||
фики функций y sin x |
и y |
1 |
(см. рис. |
|||||||||||
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||
17). Для |
уравнения |
sin x |
1 |
|
запишем |
|||||||||
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
||||
общее решение x ( 1)n |
|
n, |
n Z. |
|||||||||||
|
||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
sinx< |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
y=0,5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|||||
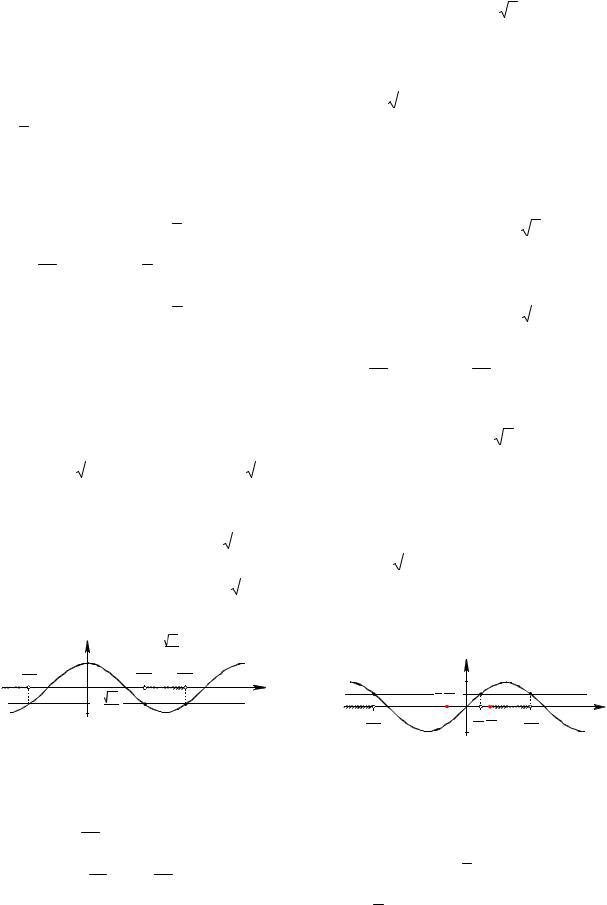
Рис. 17
Найдем три корня этого уравнения, последовательно придавая переменной n
значения –1, 0 и 1: |
7 |
, |
|
и |
5 |
. Полу- |
|
6 |
|
||||
6 |
|
6 |
|
|||
ченные значения являются абсциссами трех последовательных точек пересечения построенных графиков. Неравенство
sin x |
1 |
|
|
выполняется на промежутке |
||||||
2 |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
7 |
|
|
|
|
y sin x |
||||
|
|
; |
|
|
|
– график функции |
|
|||
6 |
|
|
|
|||||||
|
|
6 |
|
|
|
|
||||
расположен ниже прямой y |
1 |
, |
а нера- |
|||||||
|
||||||||||
|
|
|
|
|
|
2 |
|
|
||
25.12.2011 www.alexlarin.net |
16 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
венство sin x |
1 |
выполняется на проме- |
|||||
|
|||||||
|
|
|
|
2 |
|
||
|
|
|
5 |
|
|||
жутке |
|
|
; |
|
|
|
– график функции |
|
|
|
|||||
|
6 |
6 |
|
||||
y sin x расположен выше прямой
y 1 . 2
Добавляя слагаемое (период синуса) к концам этих интервалов, получаем окончательное решение:
для неравенства sin x 1 в виде
2
7 2 n x 2 n, n Z; 6 6
для неравенства sin x 1 в виде
2
|
|
2 n x |
5 |
2 n, n Z. |
|
|
|
|
|
||||||||||||||||||
6 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
На рисунке штриховкой показаны ре- |
|||||||||||||||||||||||||||
шения неравенства sin x |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 29. Решить неравенства: |
|
|
|
|
|
||||||||||||||||||||||
а) cosx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
2 |
|
; |
|
|
б) cosx |
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Схематично изобразим гра- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
фики функций |
|
|
y cosx |
и y |
|
2 |
|
|
|
(см. |
|||||||||||||||||
|
|
|
2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
рис. 18). Для уравнения |
cosx |
2 |
|
|
за- |
||||||||||||||||||||||
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y |
|
|
|
cosx< |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Рис. 18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пишем общее |
|
|
|
решение |
|
x |
3 |
2 n, |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
n Z. При n 0 найдем два корня этого
уравнения 3 , при n 1 выберем один
4
корень x 3 2 5 . Полученные
4 4
значения являются абсциссами трех последовательных точек пересечения построенных графиков.
|
Неравенство cosx |
|
|
2 |
выполняется |
||||||||||||
|
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
5 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
; |
|
|
|
|||||
на промежутке |
|
|
|
|
, а неравенство |
||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|||
cosx |
|
|
2 |
|
выполняется на промежутке |
||||||||||||
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
; |
|
|
. |
|
Добавляя слагаемое (период |
|||||||||
|
|
|
|
||||||||||||||
4 4
косинуса) к концам этих интервалов, получаем окончательное решение:
для неравенства cosx |
2 |
|
в виде |
||||||
2 |
|||||||||
|
3 |
|
5 |
|
|
|
|||
|
2 n x |
2 n, n Z; |
|||||||
4 |
|
||||||||
4 |
|
|
|
|
|
||||
для неравенства cosx |
|
2 |
|
в виде |
|||||
2 |
|
||||||||
|
|
|
|
|
|
|
|||
3 2 n x 3 2 n, n Z. 4 4
Пример 30. Решить систему
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
cosx |
|
|
, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
sin x |
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Имеем |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
cosx |
|
, |
|
x |
|
|
|
|
|
2 k, |
|
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
k,n Z . |
||||||
|
|
|
|
|
|
|
1 |
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
sin x |
|
|
, |
|
|
|
|
sin x |
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y=sinx |
|
y |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
y=0,5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
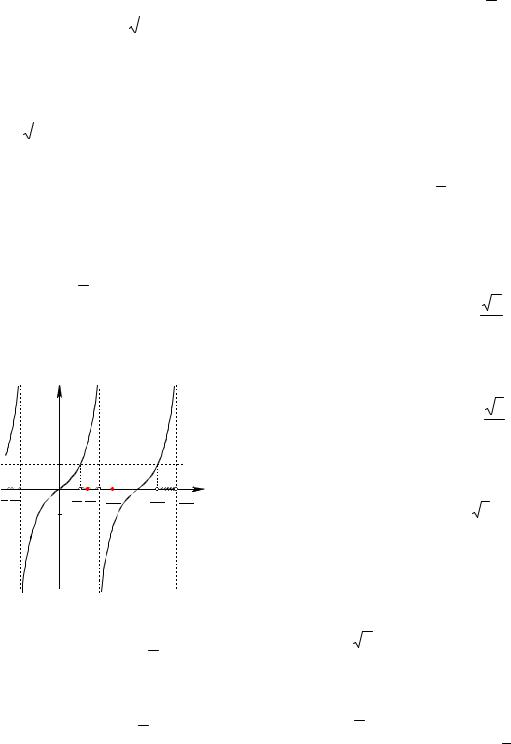
Рис. 19 |
|
|
|
|
|
||||
Из рисунка 19 видно, что на проме- |
|||||||||||||||||||
|
|
|
7 |
5 |
|
|
|
|
|
|
|
|
|
||||||
жутке |
|
; |
|
, |
длина которого |
2 , |
|||||||||||||
|
|
||||||||||||||||||
|
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|||||
неравенству sin x 1 удовлетворяет одно
2
число . Следовательно, все числа вида
4
25.12.2011 www.alexlarin.net |
17 |
Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
|
|
2 n, |
n Z |
удовлетворяют данному |
|||||||||||||||
4 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
уравнению. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Ответ: |
2 n, n Z . |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||
|
|
Пример 31. Решить систему: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
sin x |
|
|
|
, |
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx 1. |
|
|
|
|
|
|
|||||
|
|
Решение. Из условия получаем |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|||||||
|
3 |
|
|
|
|
|
|
|
|||||||||||
|
sin x |
|
|
, |
|
x ( 1) |
|
|
|
|
|
k, |
|||||||
|
|
|
|
|
3 |
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
k Z. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
tgx 1 |
|
|
|
|
tgx 1, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||
|
|
На промежутке |
|
; |
|
|
|
|
|
|
, длина кото- |
||||||||
|
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
рого 2 , неравенству tgx 1 удовлетво-
ряет одно число (см. рис. 20). Следова-
|
3 |
|
|
|
|
|
|
тельно, все |
числа |
вида |
2 n, |
n Z , |
|||
3 |
|||||||
|
|
|
|
|
|
||
удовлетворяют данной системе. |
|
|
|||||
|
y |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
Рис. 20
Ответ: 2 n, n Z . 3
Тренировочные упражнения
3. Дано уравнение sin x 1 .
2
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку [0; ].
в) Укажите корни, принадлежащие от-
|
|
3 |
|
|||
резку |
|
|
; |
|
. |
|
2 |
2 |
|||||
|
|
|
|
|||
г) Укажите корни, принадлежащие отрезку [0;4 ].
4. Дано уравнение cosx 1 .
2
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку [0; ].
в) Укажите корни, принадлежащие от-
|
|
3 |
|
|
резку |
|
|
;0 . |
|
2 |
||||
|
|
|
г) Укажите корни, принадлежащие отрезку [ 2 ;3 ].
5.Дано уравнение 
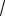 3tgx 3 0. а) Решите уравнение.
3tgx 3 0. а) Решите уравнение.
б) Укажите корни, принадлежащие от-
|
|
|
3 |
|||
резку |
|
|
; |
|
. |
|
3 |
2 |
|||||
|
|
|
|
|||
6. Дано уравнение sin3x 2 .
2
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку [0;2 ].
7. Дано уравнение cos2x 3 .
2
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку [ ; ].
8. Дано уравнение tg |
x |
|
3 |
. |
|
3 |
|||
2 |
|
|
||
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку [ 3 ;3 ].
9. Найдите те решения уравнения
sinx |
2 |
, для которых cosx 0 . |
|
2
10. Найдите те решения уравнения
cosx 1 , для которых sinx 0.
2
11. Дано уравнение 3ctg3x 
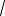 3 0. а) Решите уравнение.
3 0. а) Решите уравнение.
25.12.2011 www.alexlarin.net |
18 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
б) Укажите корни, принадлежащие от-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
резку |
|
|
; . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||
|
|
|
cos |
|
|
|
|
|
|
|
0, |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
4 |
|
|||||
12. Решите систему |
x |
|
|
|
|||||||||
|
|
|
|
|
|
||||||||
|
|
|
sin |
|
|
|
|
|
|
0. |
|||
|
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
6 |
|
||||||
|
|
|
|
|
|
||||||||
13. Найдите наименьший положительный
|
|
|
3 |
|
|
корень уравнения sin x |
|
|
|
|
. |
|
2 |
||||
|
6 |
|
|
||
14. Найдите наибольший отрицательный
|
|
|
2 |
|
|
корень уравнения cos x |
|
|
|
|
. |
|
2 |
||||
|
12 |
|
|
||
2. Основные методы решения тригонометрических уравнений
Для тригонометрических уравнений применимы общие методы решения (разложение на множители, замена переменной, функционально-графические) и равносильные преобразования общего характера.
2.1. Тригонометрические уравнения линейные относительно простейших тригонометрических функций
В данном пункте рассмотрим уравнения, содержащие синус, косинус, тангенс и котангенс степени не выше первой.
уравнения вида sin f (x) a, cos f (x) a, tg f (x) a и ctg f (x) a
Уравнения данного вида сводятся к простейшим путем замены f (x) t.
Часто задача осложняется тем, что требуется найти все решения уравнения, принадлежащие указанному промежутку.
Пример 32. Найти все корни уравнения cos4x 0,3, принадлежащие проме-
жутку 0; .
Решение. Положив 4x t , будем искать корни уравнения cost 0,3, принад-
лежащие другому промежутку 0; 4 . Решения задаются формулами
t arccos0,3 2 k , |
k Z |
или |
x arccos0,3 2 n, n Z.
Так |
как |
0 arccos0,3 |
|
и |
|
||||
|
|
2 |
|
|
arccos0,3 0, то неравенство
2
0 arccos0,3 2 k 4 справедливо при
k 0 |
и k 1. Соответственно, |
неравен- |
ство |
0 arccos0,3 2 k 4 |
справед- |
ливо при k 1 и k 2. Возвращаясь к исходной переменной, получим:
x 1arccos0,3, x 1arccos0,3
и |
4 |
|
|
|
|
|
|
4 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
1 |
arccos0,3, |
x |
1 |
|
|
arccos0,3. |
||||||
|
|
|
4 |
|
|
||||||||||
2 |
4 |
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
Ответ: |
|
arccos0,3, |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||
|
|
|
|
|
|
1 |
arccos0,3, |
1 |
arccos0,3. |
||||||
|
|
2 |
|
|
|||||||||||
|
|
4 |
|
|
4 |
|
|
||||||||
В тех случаях, когда промежутки привязаны к четвертям тригонометрической окружности, для отбора корней удобно использовать модель тригонометрической окружности.
Пример 33. Найти все корни уравне-
ния sin 2x 1 , принадлежащие проме-
2
жутку ; 2 .
Решение. Решения уравнения
sin 2x 1 запишем совокупностью двух
2
серий: x n и x 5 n, n Z .
|
|
|
|
12 |
|
12 |
|
|
|
|
|
|
||||
|
|
На числовой ок- |
|
|
|
|
|
|
||||||||
ружности (см. рис. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
21) получаем |
два |
|
|
|
|
|
|
|
||||||||
числа, |
удовлетво- |
|
|
|
|
|
|
|||||||||
ряющие |
|
|
условию |
|
|
|
|
|
||||||||
|
|
O |
|
|
|
|
|
|||||||||
задачи |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
13 |
|
|
и |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
12 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
12 |
|
|
|
|
|
|
|
|
||||||
|
5 |
|
17 |
. |
|
|
|
|
|
|
||||||
|
|
Рис. 21 |
|
|
|
|||||||||||
12 |
|
|
|
|
|
|||||||||||
|
12 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Ответ: |
13 |
, |
|
17 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|||||
|
|
|
|
|
|
|
|
|
|
12 |
|
|
||||
25.12.2011 www.alexlarin.net |
19 |

Корянов А.Г., Прокофьев А.А. Тригонометрические уравнения: методы решений и отбор корней
В некоторых простых случаях замена не обязательна.
Пример 34. Решить уравнение
|
|
|
2 |
|
||
sin |
|
x |
|
|
. |
|
4 |
2 |
|||||
|
|
|
|
|||
Решение. Используя нечетность синуса, перепишем уравнение в виде
|
|
|
2 |
|
|
sin x |
|
|
|
|
. Последнее равенство |
|
2 |
||||
|
4 |
|
|
||
выполняется |
в |
двух |
случаях: |
|||||||
x |
|
|
|
2 n |
или |
x |
|
|
|
2 n, |
|
|
|
4 |
|||||||
4 |
4 |
|
|
4 |
|
|
||||
n Z . Отсюда получаем x 2 n или
2
x 2 n, n Z .
Ответ: 2 n, 2 n, n Z.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
Тренировочные упражнения |
|||||||||||||||||||||||
15. |
|
|
Найдите |
|
|
корни |
уравнения |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3 tg x |
|
|
|
|
1, |
|
удовлетворяющие ус- |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ловию 2 x 1. |
|
|
|
|
|||||||||||||||||||||||
16. |
|
|
Найдите |
|
|
корни |
уравнения |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
4x |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
принадлежащие |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
промежутку [ ; ). |
|
|
|||||||||||||||||||||||||
17. |
|
|
Найдите |
|
|
корни |
уравнения |
||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sin 3x |
|
|
|
|
|
, |
|
|
|
принадлежащие проме- |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
жутку [ 2 ; ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
18. |
|
|
Найдите |
|
|
корни |
уравнения |
||||||||||||||||||||
|
|
|
4x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
sin |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
принадлежащие про- |
|||||||||||
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
межутку [ 2 ;2 ). |
|
|
|||||||||||||||||||||||||
19. |
|
|
Найдите |
|
|
корни |
уравнения |
||||||||||||||||||||
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
принадлежащие |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
5 |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
промежутку [ 2;9). |
|
|
|||||||||||||||||||||||||
20. |
|
|
Найдите |
|
|
корни |
уравнения |
||||||||||||||||||||
|
|
|
4x |
|
2 |
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
принадлежащие |
||||||||||
|
5 |
|
|
|
|
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
промежутку [ 8;12).
Линейные уравнения вида acosx bsin x c
Если a 0, b 0 или a 0, b 0, то линейное уравнение acosx bsin x c приводится к простейшему уравнению
sin x |
c |
или cosx |
c |
. |
|
b |
|
a |
|
Если a и b отличны от нуля, то данное линейное уравнение преобразуется к простейшему методом введения вспомо-
гательного угла. Рассмотрим этот метод на примерах.
Пример 35. Решить уравнение

 3sin x cosx 2.
3sin x cosx 2.
Решение. Данное уравнение равно-
сильно следующим: |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
sin x |
1 |
cosx 1; |
||||||||
|
|
|
3 |
|||||||||||||
2 |
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
cos |
|
sinx sin |
|
cosx 1; |
||||||||||||
|
|
|
||||||||||||||
6 |
|
|
|
6 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
sin x |
|
|
|
1. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
6 |
|
|
||||||
Отсюда получаем |
x |
|
|
|
2 n или |
|||||||||||
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|||||||
x 2 2 n, где m Z.
3
Ответ: 2 2 n, m Z.
3
Пример 36. Решить уравнение
3cosx 4sin x 2.
Решение. Данное уравнение равносильно следующим:
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
cosx |
sinx |
|
||||||||
3 |
|
4 |
|
|
|
|
|
|
2; |
||||||||
|
|
|
|
5 |
|||||||||||||
|
5 |
|
|
|
|
|
|
||||||||||
|
|
|
5 |
3 |
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
cosx |
sinx |
. |
|
|
|||||||||
|
|
|
5 |
|
|
|
|
||||||||||
|
|
|
|
|
|
5 |
|
5 |
|
|
|
||||||
Последнее уравнение представим в виде
cos cosx sin sinx 2 , 5
где arccos3 . Отсюда получаем
5
25.12.2011 www.alexlarin.net |
20 |
