Геометрические построения

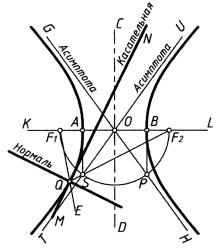
ми последовательно соединить прямыми линиями. К полученному семейству прямых подобрать с помощью лекала огибающую касательную кривую — параболу.

6.3. Гипербола

Гиперболой называется плоская разомкнутая кривая — геометрическое множество точек, разность расстояний которых от данных точек F1 и F2 равняется заданному отрезку AB. Гипербола имеет две симметричные ветви (рис. 71).

Рис. 71

Прямая, проходящая через точки A и B — вершины гиперболы, называется действительной осью, а середина отрезка AB (точка O) называется центром гиперболы; прямая CD, проведенная через центр гиперболы O перпендикулярно действительной оси AB, называется мнимой осью. Точки F1 и F2, лежащие симметрично (относительно мнимой оси) на действительной оси, называются фокусами гиперболы. Биссектриса MN угла F1QF2 (точка Q произвольная) является касательной к гиперболе в точке Q, а биссектриса смежного угла EQF2 — нормалью.

Касательные к гиперболе, точки касания которых удалены от вершины на бесконечное расстояние, называются асимптотами (TU и GH). Для их построения проводят из вершин A и B прямые, параллельные мнимой оси, до пересечения с полуокружностью, проведенной из центра O радиусом OF1. Через полученные точки S и P и центр O проводят прямые — асимптоты. Если асимптоты взаимно перпендикулярны, то гиперболу называют равнобокой.

В зависимости от заданных параметров гиперболу строят следующими способами. Способ 1. Построение по заданным вершинам A и А1 и фокусам F и F1 гиперболы при AF = A1F1. На оси гиперболы отметить ряд произвольных точек (рис. 72): 1, 2, . . . , 11, 21, . . . Точки гиперболы определяют построением на пересечении дуг, проведенных из фокусов F и F1. Радиусами дуг служат расстояния от точек до вершин гиперболы,

например: R1 = А3; R2 = А13.

Способ 2. Построение по заданной точке М в системе координат Oxy (рис. 73). Через данную точку М провести вспомогательные оси МB и МK, параллельные соответственно осям Ox и Oy. На оси МK выбрать произвольные точки 1, 2, . . . , через которые провести горизонтальные лучи. Из начала координат O провести через те же точки несколько лучей до пересечения со вспомогательной осью MB в точках

30

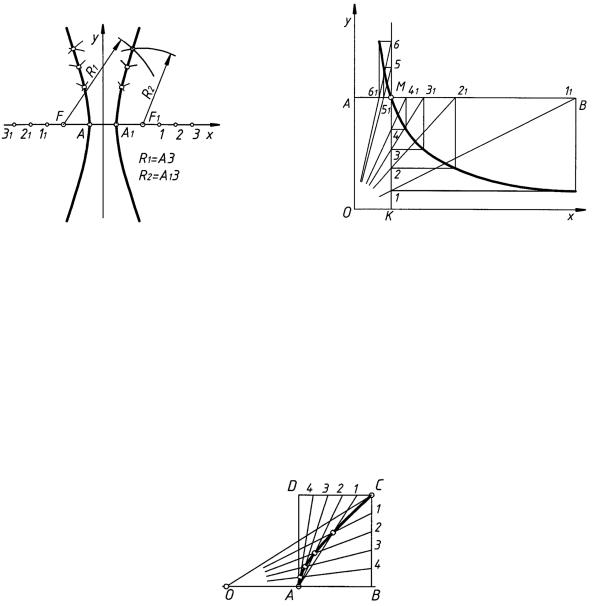
Рис. 72 Рис. 73

11, 21, . . . Опуская из этих точек перпендикуляры на горизонтальные лучи, проведенные из точек 1, 2, . . . , отметить ряд точек, принадлежащих гиперболе.

Способ 3. Построение по заданной вершине А и точке С гиперболы (рис. 74). Из точки C опустить перпендикуляр к действительной оси АВ гиперболы и построить прямоугольник ABCD. Стороны CB и DС прямоугольника разделить на одинаковое число равных частей. На оси гиперболы отложить отрезок ОА = AB и провести два пучка лучей: из точки О — к точкам деления стороны CB, из точки A — к точкам деления стороны CD. Взаимное пересечение одноименных лучей определяет положение точек гиперболы.

Рис. 74

6.4. Спирали

Спирали — плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или удаляясь от нее.

6.4.1. Спираль Архимеда

Спираль Архимеда — плоская кривая, представляющая собой траекторию точки, движущейся с постоянной скоростью от центра окружности O по радиусу, вращающемуся также с постоянной угловой скоростью (рис. 75).

Точка O называется полюсом спирали; отрезок OA — шагом спирали; отрезок KL — нормалью спирали, а прямая MN, перпендикулярная нормали, называется касательной. Точка K может располагаться в любом месте спирали, а точку L находят путем построения, для чего точку K соединяют прямой с точкой O и в точке O проводят

31

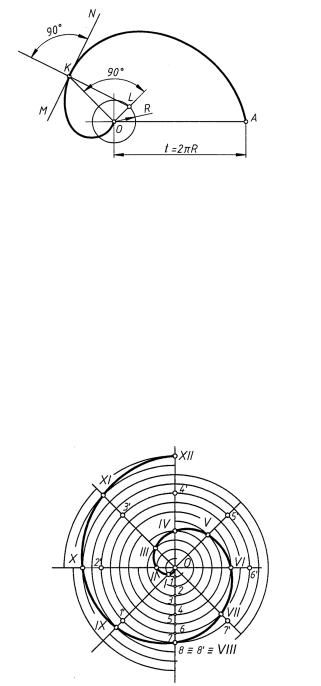
Рис. 75

перпендикуляр к отрезку KO, который пересечет в точке L окружность, проведенную через центр O, радиуса R = t/(2π).

Для построения спирали Архимеда (рис. 76) исходную окружность и ее радиус нужно разделить на одинаковое число равных частей (на рис. 76 n = 8; 1, 2, . . . , 8 — точки деления радиуса; 1 , 2 , . . . , 8 — точки деления окружности). Через точки деления на окружности провести из центра O лучи, последовательно откладывая на каждом из них соответствующее число делений радиуса: на первом луче O1 — расстояние O1, на втором луче O2 — расстояние O2 и т. д. Полученный ряд точек I, II, III, IV, V и т. д. соединить плавной кривой.

Рис. 76

Спираль Архимеда имеет две ветви. Вторая ветвь получается при вращении радиуса окружности против движения часовой стрелки.

На рис. 77 представлен чертеж детали (распределительного кулачка). Очертания его боковых сторон представляют собой спираль Архимеда.

Построение спирали Архимеда на участке между заданными точками представлено на рис. 78. Точки A и B заданы радиусами R1 и R2.

Для построения соединить точки A и B с центром O отрезками OA и OB, на большем радиусе OB отложить отрезок B1 = R2 − R1 и разделить его на произвольное число равных частей (n = 8). На столько же равных частей разделить угол AOB.

32

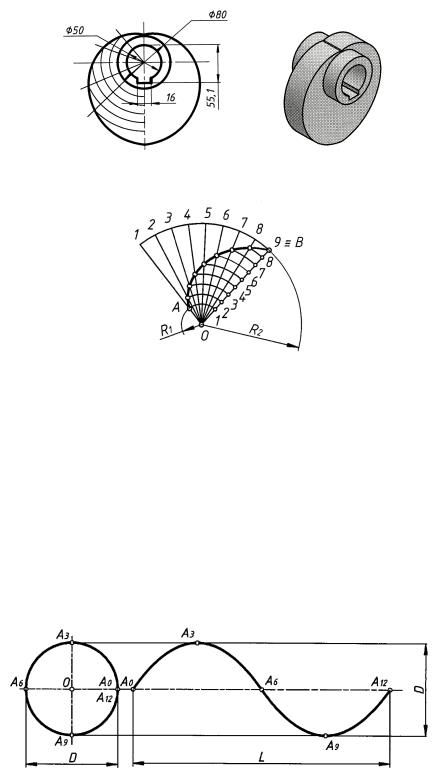
Рис. 77

Рис. 78

На пересечении лучей, делящих угол, и дуг, проведенных через точки 1, 2, . . . , 8 деления отрезка B1, отметить точки спирали Архимеда.

6.4.2. Синусоида

Синусоидой называется кривая, изображающая постепенное изменение тригонометрической функции — синуса — в зависимости от постепенного изменения величины угла (рис. 79). Прямая А0А12 называется осью синусоиды; точки А3 и A9 — вершинами синусоиды; точки А0, A6 и А12 — точками перегиба; L — длина волны, равная А0А12 (если L = πD, синусоида называется нормальной; если L > πD — вытянутой; если L < πD — сжатой). Величина D называется амплитудой синусоиды.

Рис. 79

Для построения синусоиды проводят вспомогательную окружность диаметром, равным данной амплитуде D, и на продолжении центровой линии отмечают отрезок L, равный заданной длине волны (рис. 80). Окружность делят на некоторое количество, например на 12, равных частей.

Отрезок L делят на столько же равных частей, на сколько была разделена окружность (рис. 81); из точек деления окружности проводят прямые параллельно оси сину-

33

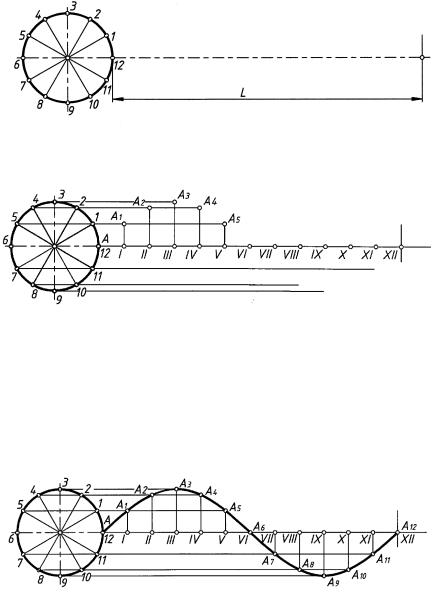
Рис. 80

Рис. 81

соиды, а из точек I, II, III, IV и V — перпендикуляры к оси до пересечения с соответствующими прямыми — получают точки А1, А2, А3, А4, А5.

Аналогичным путем находят точки А7, А8, А9, А10, А11 (точки А, А6 и А12 лежат на оси), через полученные точки проводят кривую, которая явится искомой синусоидой (рис. 82).

Рис. 82

Вид синусоид имеют многие кривые, изображающие гармонические колебательные процессы или являющиеся проекциями винтовых линий.

6.5. Циклические кривые

Циклическими называются кривые, образование которых связано с движением круга, к ним относятся циклоида, эпициклоида, гипоциклоида и др.

6.5.1. Циклоида

Циклоидой называется плоская кривая, представляющая собой траекторию движения точки, принадлежащей окружности S радиуса R, перекатываемой без проскальзывания по прямой линии. Окружность S называется производящей окружностью, а прямая MN — направляющей прямой (рис. 83). Прямая EF называется касательной к циклоиде в точке K; ее проводят через точку K и верхнюю точку вертикального диаметра производящей окружности S1. Прямая GK называется нормалью циклоиды;

34

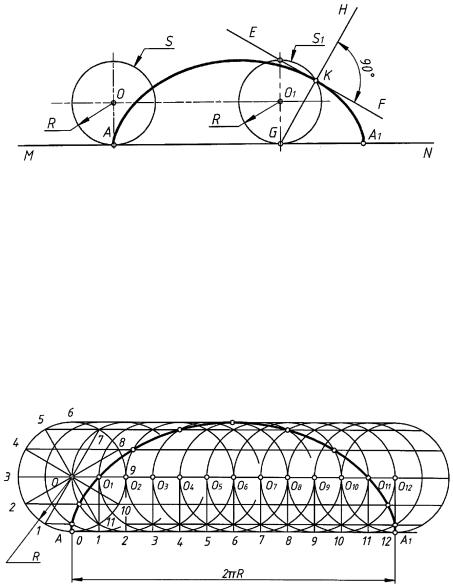
Рис. 83

ее проводят через точку K и нижнюю точку вертикального диаметра производящей окружности S1. Нормаль перпендикулярна касательной.

Для построения циклоиды (рис. 84) необходимо от начальной точки A окружности провести направляющую прямую и отложить на ней отрезок AA1, равный длине данной окружности: 2πR. Окружность и отрезок AA1 делят на одинаковое число равных частей (n = 12). Восстанавливая перпендикуляры из точек деления прямой AA1 до пересечения с прямой, проходящей через центр данной окружности параллельно AA1, отмечают ряд последовательных положений центра перекатываемой окружности O1, O2, . . . , O12.

Рис. 84

Описывая из этих центров дуги радиуса R, отмечают точки пересечения с ними прямых, проходящих параллельно отрезку AA1, через точки деления окружности 1, 2, 3 и т. д.

На пересечении горизонтальной прямой, проходящей через точку 1, с дугой, описанной из центра O1, находится одна из точек циклоиды; на пересечении горизонтальной прямой, проходящей через точку 2, с дугой, проведенной из центра O2, находится другая точка циклоиды и т. д.

6.5.2. Эпициклоида

Эпициклоидой называется плоская кривая, представляющая собой траекторию движения точки, принадлежащей окружности S радиуса r, катящейся по внешней стороне дуги радиуса R (рис. 85). Окружность S называется производящей окружностью; дуга MN называется направляющей дугой; прямая EF, проведенная через заданную точку K эпициклоиды и верхний конец E диаметра EG производящей окружности S1, имеющего радиальное направление (O0E), называется касательной к эпициклоиде.

35

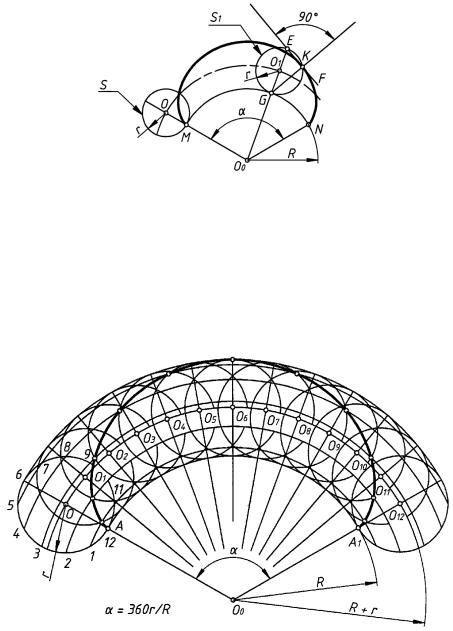
Рис. 85

Прямая GK, проходящая через точку K и нижний конец диаметра, называется нормалью эпициклоиды.

Для построения эпициклоиды производящую окружность и направляющую дугу делят на 12 частей; проводят из всех точек деления окружности концентрические дуги, центром которых является точка O0 (рис. 86).

Рис. 86

Находят точки пересечения лучей, выходящих из точки O0, с окружностью с центром в точке O0 радиуса R + r, отмечают ряд последовательных положений центра перекатываемой окружности O1, O2, . . . , O12.

Описывая из этих центров дуги радиуса r, отмечают точки пересечения с ними концентрических окружностей, проходящих через точки деления окружности 1, 2, 3 и т. д.

На пересечении концентрической окружности, проходящей через точку 1, с дугой, описанной из центра O1, находится одна из точек эпициклоиды; на пересечении концентрической окружности, проходящей через точку 2, с дугой, проведенной из центра O2, находится другая точка эпициклоиды и т. д.

Длина дуги направляющей окружности определяется центральным углом α = 360r/R. В качестве примера эпициклоиды можно указать на часть кривой профиля зуба

некоторых зубчатых колес.

36

Рис. 87

Эпициклоида, построенная при условии R = r, называется кардиоидой (рис. 87). Для любого луча, выходящего из точки 5 (см. рис. 87), справедливо равенство

12 = 1121 = 13 = 1131 = . . . = 2r. На этом основан простой способ построения кардиоиды: через точку 5 проводят лучи и на них от точек пересечения лучей с направляющей окружностью откладывают по обе стороны отрезки одинаковой длины, равные 2r.

6.5.3. Гипоциклоида

Гипоциклоидой называется плоская кривая, представляющая собой траекторию движения точки, принадлежащей окружности S радиуса r, катящейся по внутренней стороне дуги радиуса R (рис. 88). Окружность S называется производящей окружностью, дуга MN называется направляющей дугой.

Рис. 88

Прямая EF, проведенная через заданную точку K гипоциклоиды и нижний конец E диаметра EG производящей окружности S1, имеющего радиальное направление (O0E), называется касательной к гипоциклоиде. Прямая KG, проходящая через точку K и верхний конец диаметра EG, называется нормалью гипоциклоиды.

Построение гипоциклоиды (рис. 89) аналогично построению эпициклоиды при условии, что положение центров перекатываемой окружности O1, O2, . . . , O12 находят на пересечении лучей, выходящих из точки O0, с окружностью с центром в точке O0 радиуса R − r.

Гипоциклоида, полученная при условии R = 4r, называется астроидой (рис. 90). Наиболее простой приближенный способ построения астроиды основан на том, что эта кривая является огибающей для промежуточных положений отрезка, имеющего длину, равную радиусу направляющей окружности, концы которого скользят по сторонам прямого центрального угла. Для построения одной из арок астроиды необходимо

37

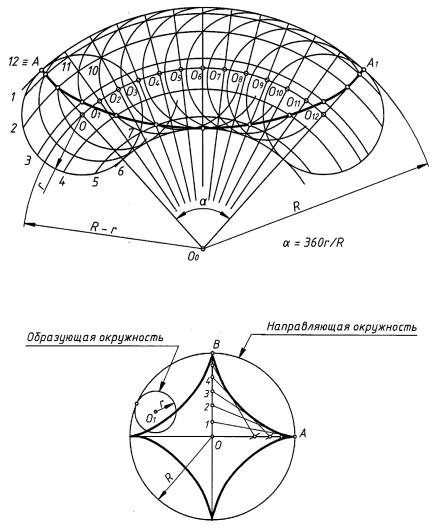
Рис. 89

Рис. 90

отложить на сторонах прямого угла отрезки равной длины OA и OB (радиус направляющей окружности R), взять на одном из отрезков произвольные точки 1, 2, 3, 4 и т. д. и, используя их в качестве центров вспомогательных окружностей (радиуса R), определить точки пересечения дуг этих окружностей с другим отрезком. Соединить каждую из взятых точек с соответствующей точкой пересечения отрезком прямой и провести огибающую семейства отрезков.

При условии R = 2r гипоциклоида трансформируется в прямую, являющуюся диаметром направляющей окружности.

7.ЦИРКУЛЬНЫЕ КРИВЫЕ

7.1.Завиток

Завитком называется циркульная кривая, имеющая очертание, близкое к очертанию эвольвенты окружности. Завиток относится к спиралям.

На рис. 91 показано построение завитков из двух, трех и шести центров или, иначе говоря, построение завитков, «глазками» которых являются окружность, правильный

38

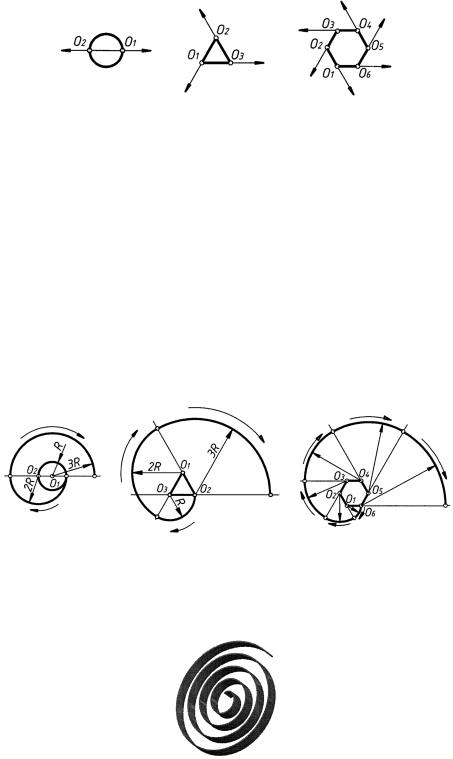
Рис. 91

треугольник и правильный шестиугольник. Из указанных видов последний вид завитка является наиболее приближенным очертанием эвольвенты окружности.

Порядок построения завитков следующий:

1)вычерчивают контур глазка и продолжают стороны фигуры глазка в одном направлении, например против движения часовой стрелки, а для окружности продолжают горизонтальную центровую в обе стороны (см. рис. 91);

2)приняв за центры вершины фигуры глазка (для окружности — ее центр и конеч-

ную точку диаметра), проводят в направлении движения часовой стрелки ряд сопряженных между собой дуг (центром первой дуги является точка О1). Радиус каждой последующей дуги увеличивается на радиус первой дуги. Отметим, что, чем большее число сторон будет иметь глазок завитка, тем более плавным получится очертание самого завитка (рис. 92).

Рис. 92

На рис. 93 показано очертание спиральной пружины (например, часовой), имеющей форму завитка.

Рис. 93

7.2. Овал

Овалом называется замкнутая выпуклая кривая, состоящая из двух основных дуг окружностей, плавно переходящих одна в другую с помощью одинаковых, симметрично расположенных дуг окружностей перехода внутреннего касания.

Если основные дуги проведены одинаковыми радиусами, то овал имеет две оси симметрии, а следовательно, и центр симметрии (рис. 94).

39