
Геометрические построения
.pdf
3.2.Определение центра окружности
Взаданной окружности (рис. 22) провести две не параллельные между собой хорды AB и CD. Через середины хорд провести перпендикуляры, пересечение которых определяет положение центра O исходной окружности.
Рис. 22
3.3.Деление окружности на три, шесть и двенадцать частей
Вокружности заданного радиуса R (рис. 23) провести через центр O взаимно перпендикулярные диаметры AB и CD. Из любой точки конца диаметра (например, из точки А) провести дугу радиуса R = АО до пересечения с окружностью в точках 1 и 2. Отрезок 12 — искомая сторона правильного вписанного треугольника 1В2.
Рис. 23
Отрезки A1 = A2 и C1 = D2 соответственно равны сторонам правильных вписанных шестиугольника и двеннадцатиугольника. Для построения недостающих вершин многоугольников достаточно провести из противоположного конца диаметра окружности (в нашем случае — из точки B) дугу того же радиуса R до пересечения с окружностью.
3.4. Деление окружности на четыре и восемь частей
Провести два взаимно перпендикулярных диаметра AB и CD (рис. 24). Отрезки AC = CB = BD = DA, соединяющие концы диаметров, являются сторонами правильного вписанного четырехугольника.
10

Рис. 24
Для деления окружности на восемь частей необходимо построить перпендикуляры к серединам сторон четырехугольника и продолжить их до пересечения с окружностью. Отрезок AM — сторона правильного восьмиугольника, вписанного в окружность.
3.5. Деление окружности на пять и десять частей
Провести два взаимно перпендикулярных диаметра AB и CD (рис. 25) и разделить радиус OB пополам в точке M. Из точки M, как из центра, провести дугу радиуса MC до пересечения ее с диаметром AB в точке K. Отрезок CK равен стороне правильного вписанного пятиугольника, отрезок OK равен стороне правильного вписанного десятиугольника.
Рис. 25
3.6. Деление окружности на семь частей
Из точек A и B концов горизонтального диаметра AB (рис. 26) провести дуги радиуса R = AO = BO и отметить точки их пересечения 1 и 2 с исходной окружностью.
Рис. 26
11
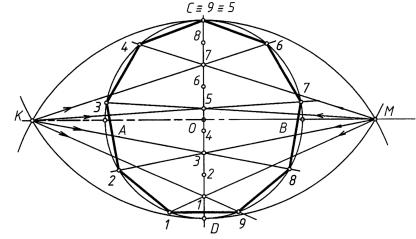
На пересечении хорды 12 с радиусом OD отметить точку M. Отрезок OM равен стороне правильного вписанного семиугольника. Для его построения измерителем последовательно отложить соответствующие отрезки на исходной окружности.
3.7. Деление окружности на n равных частей
Провести в окружности заданного радиуса R два взаимно перпендикулярных диаметра AB и СD (рис. 27) и разделить один из диаметров, например CD, на заданное число равных частей (n = 9). Из точек C и D, как из центров, провести дуги окружностей радиуса 2R до их пересечения с диаметром AB в точках K и M.
Рис. 27
Используя полученные точки K и M в качестве центров, провести семейство лучей через четные или нечетные (как в нашем случае) точки деления диаметра CD до пересечения с заданной окружностью. Полученные на окружности точки 1, 2, . . . , 9 — искомые точки деления окружности на заданное число частей. Описанный способ приближенный; дуги, на которые разделена окружность, в действительности не равны одна другой. Однако погрешность не превышает 0,01R, что для практических целей можно считать достаточным.
3.8. Построение правильных многоугольников по заданной стороне
Сторону AB (рис. 28) разделить точкой O пополам и восстановить в этой точке перпендикуляр к отрезку AB. Из точек A и B провести дуги радиуса R = AB до пересечения их в точке 1. Треугольник A1B — искомый равносторонний треугольник.
Для построения квадрата надо восстановить в точках A и B перпендикуляры к отрезку AB и продолжить их до пересечения в точках C и D с дугами радиуса R = AB. Квадрат ACDB искомый.
В квадрате ACDB провести диагонали и отметить точку 2 их пересечения. Разделить расстояние между точками 1 и 2 пополам точкой 3, которая будет служить центром окружности для вписанного в нее правильного пятиугольника со стороной AB.
Последовательно откладывая расстояние 13 от точки 1 вверх по перпендикуляру, отметить точки 4, 5, 6, . . . , n, которые будут служить центрами окружностей для
12
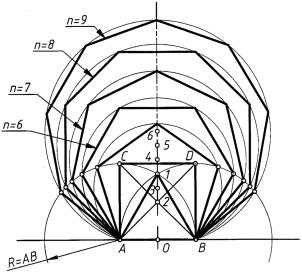
Рис. 28
построения соответственно семи-, восьми-, девятиугольника и т. д. с заданной стороной AB. Радиусами проводимых при этом окружностей являются расстояния от точки A до соответствующих центров.
4.СОПРЯЖЕНИЯ
4.1.Алгоритм построения cопряжений
Сопряжение — плавный переход одной линии в другую либо непосредственно, либо с помощью промежуточных дуг окружностей, называемых дугами сопряжения, радиусы в этом случае называют радиусами сопряжения.
Точка сопряжения — общая точка двух сопрягающихся линий, в которой одна линия переходит в другую и через которую проходит их общая касательная.
Центр сопряжения — центр дуги окружности, сопрягающей две линии. Его находят на пересечении двух геометрических фигур, каждая из которых является множеством точек плоскости, равноудаленных на заданное расстояние от одной из сопрягаемых линий.
Построения сопряжений с непосредственным переходом одной линии в другую являются не чем иным, как построением касательных: прямой, касательной к окружности, и окружности, касательной к другой окружности.
Рассмотрим переходы:
а) прямой в дугу окружности (или дуги окружности в прямую) (рис. 29). Точкой сопряжения K является точка касания, она находится в основании перпендикуляра, опущенного из центра O окружности на данную прямую. Где бы ни была проведена окружность радиуса R, плавно переходящая в данную прямую, всегда расстояние от ее центра O до заданной прямой равно R, т. е. геометрическим множеством центров O является прямая, проведенная параллельно данной прямой на расстоянии радиуса R;
б) одной дуги окружности внешнего касания в другую (рис. 30). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной. Точкой сопряжения K является точка касания, она находится на пересечении сопрягаемых дуг линией их центров OO1. Где бы ни была проведена дуга
13
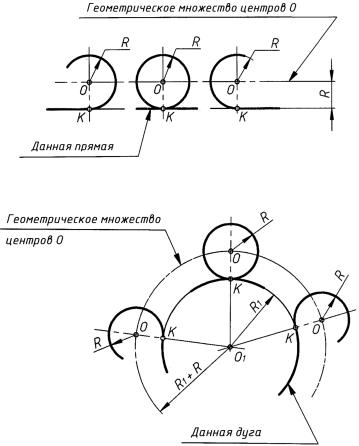
Рис. 29
Рис. 30
окружности радиуса R, расположенная с внешней стороны данной дуги окружности радиуса R1 и плавно переходящая в данную дугу, всегда расстояние от ее центра O до данной дуги равно ее радиусу R. Следовательно, геометрическим множеством центров O таких дуг окружностей будет концентрическая дуга окружности, расположенная с внешней стороны данной дуги на расстоянии радиуса R. Радиус этой дуги, а следовательно и расстояние между центрами O и O1, равен сумме радиусов R1 + R сопрягаемых дуг;
в) одной дуги окружности внутреннего касания в другую (рис. 31). Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной. Точкой K сопряжения является точка касания сопрягаемых дуг, она находится на пересечении этих дуг линией, являющейся продолжением линии центров OO1. Где бы ни была проведена дуга окружности радиуса R, расположенная внутри данной дуги окружности радиуса R1 и плавно переходящая в данную дугу, всегда расстояние от ее центра O до данной дуги равно ее радиусу R. Следовательно, геометрическим множеством центров O таких дуг будет концентрическая дуга окружности, расположенная внутри данной дуги и отстоящая от нее на величину радиуса R, т. е. радиус этой дуги (а следовательно, и расстояние между центрами O1 и O) будет равен разности радиусов R1 − R.
На основании изложенного можно сформулировать алгоритм построения сопряжения двух линий при заданном радиусе сопряжения:
1) построение множества точек, находящихся на расстоянии радиуса сопряжения от первой из сопрягаемых линий;
14
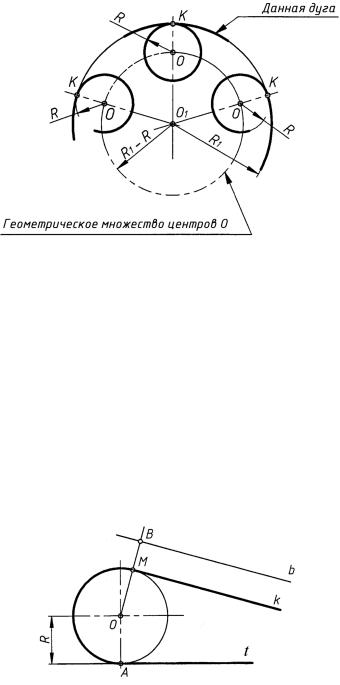
Рис. 31
2)построение множества точек, находящихся на расстоянии радиуса сопряжения от второй из сопрягаемых линий;
3)определение центра сопряжения на пересечении этих множеств;
4)определение точек сопряжения на сопрягаемых линиях; проведение дуги сопряжения между точками сопряжения.
4.2. Построение прямой, касательной к окружности
Прямая, касательная к окружности, составляет угол 90◦ с радиусом, проведенным
вточку касания. Таким образом, для построения прямой t, касающейся окружности
взаданной точке A, надо провести искомую прямую перпендикулярно радиусу OA (рис. 32).
Рис. 32
Для проведения касательной к окружности, параллельной заданной прямой b, достаточно найти точку сопряжения M на пересечении заданной окружности с перпендикуляром к прямой, опущенным из центра O: b OB; k OB; k||b.
4.3. Сопряжение пересекающихся прямых с помощью дуги окружности заданного радиуса R
Для нахождения центра O сопрягающей окружности (рис. 33) строим геометрическое множество точек, отстоящее от прямой m на расстояние R. Строим геометрическое множество точек, отстоящее от прямой n на расстояние R. На пересечении двух множеств находим точку O — центр дуги сопряжения. Точки сопряжения A и B лежат в
15
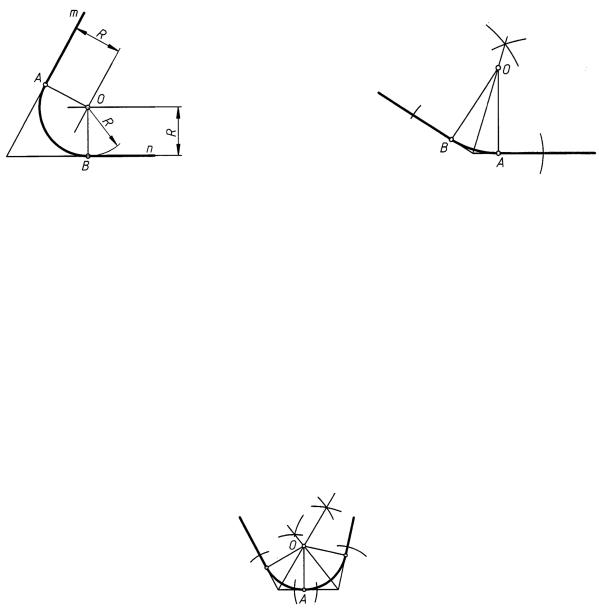
Рис. 33 |
Рис. 34 |
основании перпендикуляров, проведенных к исходным прямым, и ограничивают дугу сопряжения.
Если положение одной из точек сопряжения задано (рис. 34, точка A), а радиус сопряжения не указан, то искомый центр O находится на пересечении перпендикуляра к прямой, проведенного из точки A, и биссектрисы угла, образованного заданными прямыми (построение биссектрисы см. на рис. 13).
4.4. Сопряжение трех пересекающихся прямых
Положение центра сопрягаемой окружности (рис. 35) определяется точкой пересечения биссектрис углов. Радиус окружности (дуги´ сопряжения) равен длине перпендикуляра, опущенного из центра O на любую из трех заданных прямых.
Рис. 35
4.5. Сопряжение окружности и прямой с помощью дуги окружности заданного радиуса R
Внешнее касание (рис. 36, а). Центр O дуги сопряжения находится на пересечении двух геометрических множеств точек: вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R, и дуги´ радиуса R1 + R, проведенного из центра O1. Точки сопряжения K и M находятся соответственно в основании перпендикуляра OK и на пересечении прямой O1O с основной окружностью.
Внутреннее касание (рис. 36, б). Центр O дуги сопряжения находится на пересечении двух геометрических множеств точек: вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R, и дуги´ радиуса R1 −R, проведенной из центра O. Точки сопряжения K и M находятся соответственно в основании перпендикуляра OK и на пересечении продолжения луча O1O с основной окружностью.
16
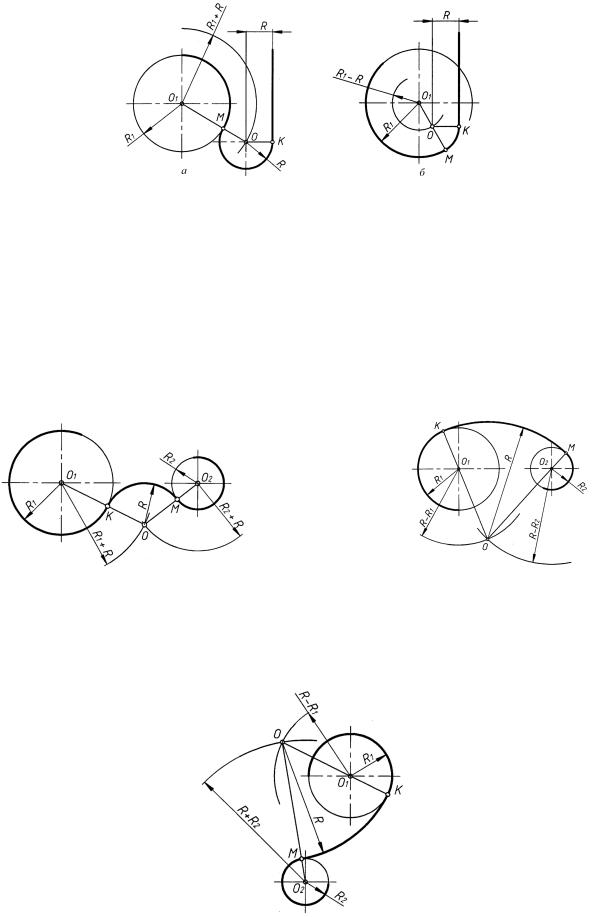
Рис. 36
4.6. Сопряжение двух окружностей с помощью дуги окружности заданного радиуса R
Внешнее касание (рис. 37). Центр O искомой дуги радиуса R находится на пересечении двух геометрических множеств точек — двух вспомогательных окружностей,
описанных из центров O1 и O2 соответствующими радиусами R1 + R и R2 + R. Внутреннее касание (рис. 38). Центр O искомой дуги радиуса R находится на пере-
сечении двух геометрических множеств точек — двух вспомогательных окружностей, описанных из центров O1 и O2 соответствующими радиусами R − R1 и R − R2.
Рис. 37 Рис. 38
Смешанное касание (внешнее и внутреннее) (рис. 39). Центр O искомой дуги радиуса R находится на пересечении двух геометрических множеств точек — двух вспомогательных окружностей, описанных из центров O1 и O2 соответствующими
Рис. 39
17
радиусами R − R1 и R + R2. Для всех случаев точки сопряжения K и M лежат на линиях, соединяющих центры сопрягаемых окружностей.
4.7. Построение касательной к окружности, проведенной через заданную точку, лежащую вне окружности
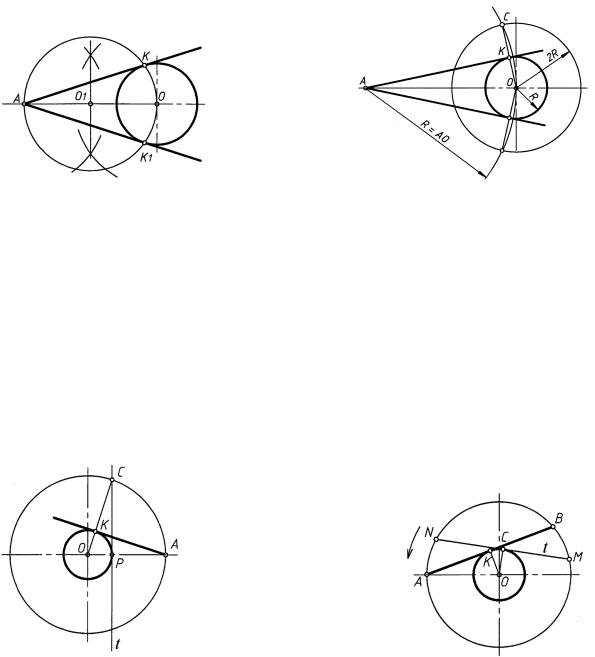
Способ 1 (рис. 40). Точки сопряжения K и K1 расположены на окружности при ее пересечении со вспомогательной окружностью, диаметр которой равен AO (вписанный в окружность угол равен половине центрального угла, следовательно, угол OKA прямой, AK — касательная).
Рис. 40 |
Рис. 41 |
Способ 2 (рис. 41). Точка сопряжения К расположена на окружности при ее пересечении с отрезком OC. Точка C — точка пересечения первой вспомогательной окружности с центром в точке O, радиус которой в 2 раза больше радиуса заданной окружности, и второй вспомогательной окружности с центром в точке A радиуса AO (точка K является серединой отрезка OC основания равнобедренного треугольника CAO, следовательно, угол OKA прямой, AK — касательная).
Способ 3 (рис. 42). Точка сопряжения K расположена на окружности при ее пересечении с отрезком OC. Точка C — точка пересечения вспомогательной окружности с центром в точке O радиуса OA с касательной t (треугольники OPC и OKA конгруэнтны, так как имеют общий угол при вершине O, заключенный между равными сторонами OP = OK, OC = OA, но треугольник OPC прямоугольный (угол при вершине P = 90◦), поэтому угол К = 90◦, AK — касательная).
Рис. 42 Рис. 43
Способ 4 (рис. 43). Точка сопряжения K получена вращением вокруг точки O касательной t в произвольной точке С заданной окружности до совмещения точки N с точкой A. Точка С займет положение точки K; AK — касательная.
18
4.8. Построение касательной к двум окружностям
Эта задача сводится к задаче на построение касательной к окружности, проведенной через заданную точку, лежащую вне окружности (см. разд. 4.7).
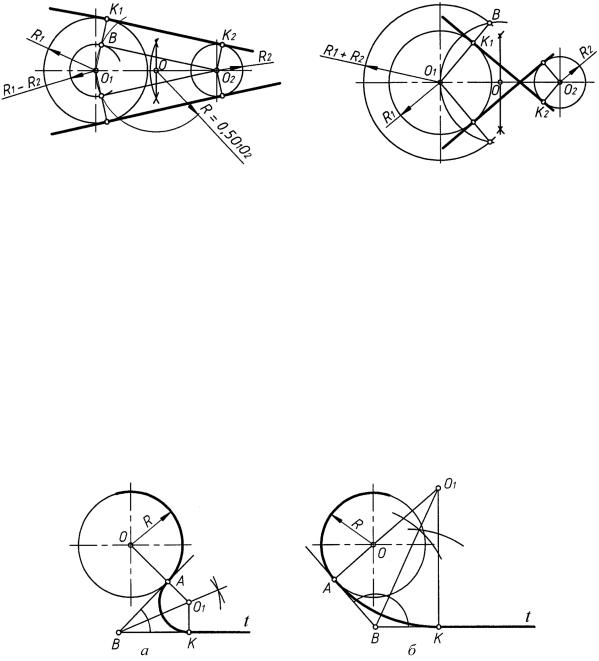
Внешнее касание (рис. 44). Из центра O1 большей окружности построить вспомогательную окружность радиуса R1 − R2. Разделить отрезок O1O2 пополам в точке O и провести вторую вспомогательную окружность радиуса R = OO1. Точка B пересечения вспомогательных окружностей определяет направление радиуса O1K1, где K1 — искомая точка сопряжения для окружности радиуса R1. Для построения точки сопряжения K2 для окружности радиуса R2 достаточно из центра O2 провести радиус O2K2 параллельно радиусу O1K1 до пересечения с окружностью радиуса R2.
Рис. 44 |
Рис. 45 |
Внутреннее касание (рис. 45). Из центра O1 большей окружности построить вспомогательную окружность радиуса R1 +R2. Далее выполнить построения в соответствии
срис. 44.
4.9.Сопряжение окружности и прямой при условии, что дуга сопряжения
проходит через заданную точку на окружности
Центр дуги сопряжения O1 (рис. 46, а — внешнее касание; рис. 46, б — внутреннее касание) определяется точкой пересечения прямой OA, проведенной через точку сопряжения A и центр O заданной окружности, и биссектрисы угла ABK, образованного касательной AB в точке сопряжения A и заданной прямой t. Радиус сопрягающей дуги равен расстоянию O1A; O1K t, где точка K — точка сопряжения на прямой t.
Рис. 46
19
