
integral
.pdf
n
Площадью поверхности Ω назовём предел суммы ωT = ∑| ωi |, где | ωi| −
i=1
площадь площадки ωi, когда диаметры этих площадок (или, соответственно,
площадок Di) стремятся к нулю, т.е. когда dT → 0.
Нормаль к поверхности F(x,y,z) = z − f (x,y) = 0 задаётся градиентом в точ-
ке Мi:
|
|
|
|
∂F |
, |
∂F |
, |
∂F |
|
− |
∂f |
, − |
∂f |
|
|
|
|
|
|
|||
grad F = |
|
∂x |
∂y |
∂z |
= |
∂x |
∂y |
, 1 . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Запишем единичный вектор n нормали: |
|
|
|
|
|
|
|
|||||||||||||||
n = |
|
grad f |
|
= (cosα, cos β, cosγ ), |
|
|
gradf |
|
|
∂f 2 |
|
∂f 2 |
||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
= |
|
|
+ |
+1 . |
||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
grad f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Теперь можно найти угол γ, (γ <π / 2 ), который нормаль образует с осью OZ: |
||||||||||||||||||||||
cosγ = |
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||
( fx′)2 +(f y′ )2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Поскольку Di − проекция ωi на плоскость OXY, то Di = ωi cos γ, (рис. 20б).
Тогда
ωT |
= ∑ |
|
ωi |
|
= ∑ |
| Di | |
= ∑ |
1 |
|
| Di | |
|
→ |
|
|
|
|
|
|
|
||||||||||
cosγ |
cosγ |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
d →0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
→→0 |
∫∫ |
dxdy |
= ∫∫ 1+ fx′2 + f y′2 dxdy. |
|
|
|
|
|
|
|
|
|
d |
|
cosγ |
||||
|
|
|
|
|
|
|
|
|
T |
D |
|
|
D |
|
Таким образом, площадь поверхности Ω, заданной уравнением z = f (x,y) |
||||||||||||||
вычисляется по формуле: |
|
|
|
|
|
|
|
|
||||||
|
| Ω|= ∫∫ 1 + fx′2 + f y′2 dxdy , |
|
|
|
(1) |
|||||||||
|
|
|
D |
|
|
|
|
|
|
|
|
|||
где D − ортогональная проекция области Ω на плоскость OXY.
36
Отметим без доказательства, что если поверхность Ω на ограниченной об-
ласти в плоскости переменных (u, v) задана параметрически с помощью со-
отношений:
х = φ(u,v), y = ψ(u,v), z = χ(u,v),
то ее площадь может быть найдена по формуле: |
|
| Ω|= ∫∫ ЕG − F 2 dud v , |
(2) |
где E =ϕu′2 +ψu′2 + χu′2 , G =ϕv′2 +ψv′2 + χv′2 , |
F =ϕu′ϕv′ +ψu′ψv′ + χu′ χv′ − так |
называемые гауссовские коэффициенты поверхности Ω.
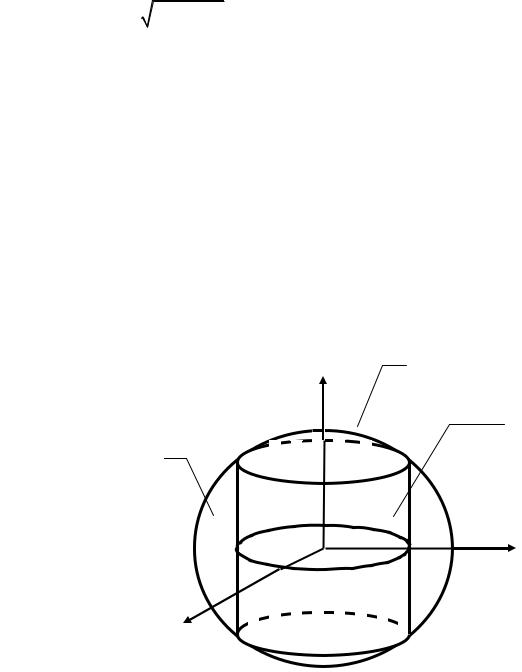
ПРИМЕР 1. Найти площадь части Ω сферы x2 + y2 + z2 = a2, заключенной внутри прямого кругового цилиндра x2 + y2 = b2 , b ≤ a (рис. 21).
Из симметрии относительно плоскости ОХY для нахождения искомой площади поверхности достаточно вычислить площадь ее части Ω1, лежащей выше плоскости ОХY, и удвоить полученное значение.
Ω1
z
x2 + y2 = b2
x2 + y2 + z2 = a2
y
D
x
Рис.21. К примеру 1.
37
Из уравнения верхней полусферы получаем:
z = a2 − x2 − y2 z′x = |
|
|
|
−x |
|
|
|
|
, |
z′y = |
|
|
−y |
|
|
|
. |
|||||||||||||||
|
a2 − x2 |
|
|
|
a |
|
− x2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− y2 |
|
|
|
2 |
− y2 |
||||||||||||||||
Подставляя эти значения в формулу (1), находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
| Ω|= 2 | Ω1 |= 2∫∫ |
1+(z′x )2 +(z′y )2 dxdy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−x |
|
|
|
2 |
|
|
|
|
|
−y |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
= 2∫∫ |
1+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
dxdy = |
|
|
|
|
|
|
|
|||||||
|
2 |
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
D |
|
a |
− x |
− y |
|
|
|
a |
− x |
− y |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
dxdy |
|
|
|
|
2π |
b |
|
rdr |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= 2a∫∫ |
|
|
|
|
|
|
= 2a ∫ |
dϕ |
∫ |
|
|
|
|
|
|
|
= 4πa a − |
|
a |
|
−b |
|
. |
|||||||||
|
− x2 − y2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
D a2 |
|
|
|
0 |
0 a2 |
− r2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Здесь D – проекция рассматриваемой поверхности на плоскость ОХY, т.е. круг радиуса b с центром в начале координат, который вырезает на плоскости ОХY
цилиндр x2 + y2 = b2. Двойной интеграл был вычислен с помощью перехода к полярным координатам.
Замечание. Строго говоря, область D в примере 1 не удовлетворяет условиям, накладываемым на области при переходе к полярным координатам, а именно, она содержит начало координат (см. рис. 16). Тем не менее, полученный в примере 1 результат остается справедливым. Для его обоснования следо-
вало бы вырезать из области D некоторую малую окрестность точки (0,0), на-
пример круг радиуса ε с центром в этой точке, а затем провести предельный пе-
реход при ε→0.
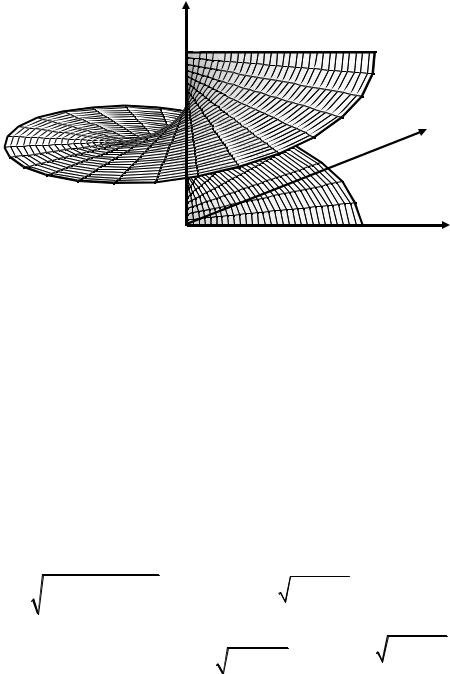
ПРИМЕР 2. Найти площадь поверхности геликоида (рис. 22), заданного параметрическими уравнениями:
x = r cos φ, y = r sin φ, z = b φ, 0 < r ≤ a, 0 ≤ φ < 2π.
38
z
y
O |
x |
|
Рис.22. Геликоид.
Поскольку xr′ = cosϕ, xϕ′ = −r sinϕ, yr′ = sinϕ, |
yϕ′ |
= r cosϕ, |
zr′ = 0, |
zϕ′ = b , |
||||||
получаем по формуле (2): |
|
|
|
|
|
|
|
|||
|
E = cos2 ϕ +sin2 ϕ =1, |
|
|
|
|
|
|
|
||
G = r2 sin2 ϕ + r2 cos2 ϕ +b2 = r2 +b2 , |
|
|
|
|
|
|||||
|
F = −r cosϕsinϕ + r sinϕ cosϕ +0 b = 0. |
|
|
|
|
|
||||
Отсюда имеем площадь поверхности геликоида |
|
|
|
|
|
|
||||
|
|
|
2π |
a |
|
|
|
|
|
|
|
Ω |
|
= ∫∫ 1 (r2 +b2 )−0 drdϕ = ∫ |
dϕ∫ |
r |
2 +b2 dr = |
|
|
|
|
|
|
|
|
|
|
|||||
0 |
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
=π a a2 +b2 +b2 ln a + |
a |
|
+b |
. |
|||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(По поводу справедливости включения в пределы интегрирования точек r=0 и
ϕ=2π см. замечание к примеру 1).
39
4.5. Несобственные кратные интегралы.
Как и обычные несобственные интегралы, кратные несобственные интегралы бывают двух типов: с неограниченной областью интегрирования и с неограниченной подынтегральной функцией. Рассмотрим каждый из типов таких интегралов:
Несобственные интегралы с неограниченной областью интегрирова-
ния. Пусть D − неограниченная область, а {Dn} − произвольная последова-
тельность вложенных друг в друга ограниченных областей с «хорошими» границами (определение «хорошей» границы было дано в п. 4.1), причем эта по-
∞
следовательность «исчерпывает» область D , т.е D = Dn и D1 D2 …
n=1
… Dn … . Пусть, кроме того, функция f(x,y) непрерывна на области D. То-
гда несобственный двойной интеграл ∫∫ f (x, y)dxdy определяется как предел
D
последовательности интегралов ∫∫ f (x, y)dxdy при n → ∞. Интеграл считается
Dn
сходящимся, если этот предел существует, конечен и не зависит от выбора по-
следовательности областей {Dn}.
Несобственные интегралы с неограниченной подынтегральной функ-
цией. Пусть теперь D − ограниченная область, но при этом функция f(x,y) не
ограничена в окрестности точки М D. Обозначим через δ окрестность точки
М с диаметром δ, лежащую внутри области D. Тогда несобственный двойной
интеграл от неограниченной функции f(x,y) определяется как следующий предел:
∫∫ f (x, y)dxdy = lim ∫∫ f (x, y)dxdy , |
|
D |
δ→0D\ δ |
40
если этот предел существует и не зависит от выбора окрестностей δ. (Напом-
ним, что область D \ δ состоит из точек, принадлежащих области D, но не принадлежащих области δ ).
Аналогично могут быть определены несобственные тройные интегралы.
Для несобственных кратных интегралов, подобно тому, как это делалось ранее, можно определить понятие абсолютной сходимости, а также сформулировать теоремы сравнения.
ПРИМЕР 1. Исследовать на сходимость интеграл I = ∫∫ |
dxdy |
. |
||
(1+ x2 |
+ y2 )α |
|||
2 |
|
|||
Используем определение. В качестве областей Dn возьмем круги радиусов n, т.е. Dn={ х2+ у2 ≤ n2 }. Имеем D1 D2 D3 … Dn R2… и Dn → R2
при n → ∞. Таким образом, области Dn можно использовать для определения интеграла I:
|
|
|
|
dxdy |
|
|
|
|
|
|
ρd ρdϕ |
|
2π |
n |
ρd ρ |
|
|
|||||||
In = ∫∫ |
|
|
|
|
|
= ∫∫ |
= ∫ dϕ∫ |
|
= |
|||||||||||||||
|
|
2 |
|
|
|
2 |
α |
2 α |
2 |
α |
||||||||||||||
|
D |
(1+ x |
|
+ y |
|
) |
|
D |
(1+ ρ |
) |
|
|
0 |
0 |
(1+ ρ |
) |
|
|||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
, при α ≠ 1; |
|||||||
n |
d(1+ ρ |
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|||||||
|
|
|
|
|
|
|
α−1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
=π0∫ |
|
|
|
= |
1−α |
(1+ n2 ) |
|
|
|
|
|
|
|
|
||||||||||
(1+ ρ 2 )α |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π ln (1+ n |
2 |
), |
|
при α = 1. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞, |
|
|
|
|
α ≤1; |
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
In |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
, α |
>1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
α − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
41

Таким образом, при α ≤ 1 интеграл I расходится, а при α > 1 сходится и имеет значение απ−1 .
Формулы интегрирования под знаком интеграла позволяют, в частности, вычислить важный интеграл Лапласа, подынтегральная функция которого не может быть проинтегрирована в элементарных функциях:
ПРИМЕР 2. Вычислить интеграл Лапласа: I = ∞∫e−x2 dx.
0
Пусть область D представляет собой первый квадрант плоскости OXY. Запишем двойной интеграл
|
e−x |
2 |
−y |
2 |
dxdy = |
∞ ∞ |
e−x |
2 |
−y |
2 |
dy = |
∞ |
e−x |
2 |
dx × |
∞ |
e−y |
2 |
∞ |
e−x |
2 |
2 |
||||
∫∫ |
|
|
∫ |
dx |
∫ |
|
|
∫ |
|
∫ |
|
dy = |
∫ |
|
dx |
= I 2 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
D |
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
Перейдем в двойном интеграле к полярным координатам:
|
|
∞ |
π / 2 |
dϕ e−r2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
I 2 = ∫∫e−x2 −y2 dxdy = ∫ rdr ∫ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||
D |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
π |
∞ |
−r2 |
dr = |
π |
|
1 ∞ |
−r2 |
dr |
2 |
= − |
π |
e |
−r2 |
|
∞ |
π |
. |
||
|
||||||||||||||||||||
2 |
∫ re |
|
2 |
2 |
∫ e |
|
|
4 |
|
|
= |
4 |
||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда получаем интеграл Лапласа:
∞ |
π |
|
|
I = ∫ e−x2 dx = |
. |
||
2 |
|||
0 |
|
||
|
|
42

Теоретические вопросы к главе 4.
1.По какой переменной взят внешний интеграл в повторном интеграле:
1 |
2x+1 |
f (x, y) |
dxdy ? |
|
|
|
∫ |
∫ |
|
|
|
||
0 |
x2 |
|
|
|
|
|
2. Какой |
из |
интегралов |
больше: |
∫∫ 1+ x2 + y2 dxdy |
или |
|
|
|
|
|
|
G |
|
∫∫ 1+ x4 + y4 dxdy , если область G – прямоугольник: 0 ≤ x ≤1 , 0 ≤ y ≤1 ?
1+ x4 + y4 dxdy , если область G – прямоугольник: 0 ≤ x ≤1 , 0 ≤ y ≤1 ?
G
3.Показать, что если область G представляет собой прямоугольник: – 1 ≤
≤ x ≤1, – 1 ≤ y ≤ 1, то двойной интеграл ∫∫xm yndxdy обращается в нуль,
|
G |
|
|
если хотя бы одно из чисел m или n нечетно. |
|
|
|
a |
x |
a |
a |
4. Доказать формулу Дирихле: ∫dx∫ f (x, y)dy = ∫dy ∫ f (x, y)dx . |
|||
0 |
0 |
0 |
y |
5.Пользуясь формулой Дирихле, доказать равенство:
a |
x |
a |
∫dx∫ f (y)dy = ∫(a − y) f ( y)dy . |
||
0 |
0 |
0 |
6.Вычислить интеграл ∫∫ f (x, y)dxdy , если область G представляет собой
G
прямоугольник: a ≤ x ≤ b , c ≤ y ≤ d, а функция f (x, y) = Fxy′′(x, y) .
7.Доказать, что, если G – прямоугольник: a ≤ x ≤ b , c ≤ y ≤ d , то
|
b |
|
|
|
d |
|
∫∫ f (x)g( y)dxdy = |
|
f (x)dx |
|
|
|
|
∫ |
|
∫g( y)dy |
. |
|||
G |
a |
|
|
|
c |
|
43
8.Найти среднее значение функции f (x, y) в области G :
а) f (x, y) = |
sin3 x sin3 y |
, |
G – прямоугольник: 0 ≤ x ≤ π/4 , 0 ≤ y ≤ π/4; |
||
cos8 |
y |
||||
|
|
|
|||
б) f (x, y) = x e2x+y , |
G – прямоугольник: – 1 ≤ x ≤ 1, – 1 ≤ y ≤ 1; |
||||
в) f (x, y) = x – 2 y, G – треугольник с вершинами А(1,0), В(1,1), С(3,1) .
9. Оценить величину интеграла: |
|
∫∫ |
|
dxdy |
|
. |
|
|
|
1+sin2 x +cos2 |
|
||||
x |
2 |
+y |
2 |
≤4 |
y |
||
|
|
|
|
|
|||
Задачи к главе 4.
Изменить порядок интегрирования в повторных интегралах:
|
3 |
5+ 3+2 y − y 2 |
|
0 |
x+4 |
|
4 |
4−x |
|||
1. |
∫ dy |
|
|
∫ f (x, y)dx . |
2. |
∫ dx ∫ f (x, y)dy + ∫dx ∫ f (x, y)dy . |
|||||
|
−1 |
5− 3+2 y −y 2 |
|
−4 − x+4 |
0 − 4−x |
||||||
|
0 |
4−y2 |
|
|
|
5 |
y |
|
|
||
3. ∫ dy |
|
∫ |
f (x, y)dx . |
|
4. ∫dy ∫ f (x, y)dx. |
|
|||||
|
−2 − −2 y−y2 |
|
|
|
0 y 5 |
|
|
||||
|
4 3 |
y 2 +1 |
|
|
1 |
1−y2 −1 |
|
|
|||
5. |
∫ dy ∫ f (x, y)dx . |
6. |
∫dy |
∫ f (x, y)dx . |
|
|
|||||
|
0 |
5 y−5 |
|
|
0 − 2 y−y2 |
|
|
||||
|
5 2 |
x2 5 |
|
|
−1 2x+3 |
|
0 |
2x+3 |
|||
7. |
∫ dx ∫ f (x, y)dy . |
8. |
∫ dx ∫ f (x, y)dy + ∫ dx ∫ f (x, y)dy . |
||||||||
|
−5 2 |
x |
2 |
−5 |
|
|
−2 |
2 x |
|
−1 |
−2 |
|
|
|
|
|
|
|
|
|
|
||
Перейти к полярным координатам и расставить пределы интегрирования по новым переменным в интегралах:
9. |
1 dx1 |
f |
x2 + y2 dy . |
|
|
∫ |
∫ |
|
|
|
0 |
0 |
|
|
44
|
1 |
2 |
|
|
|
|
3 |
−x2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 ∫ |
|
|
|
f |
|
x2 + y2 dy . |
||||||
10. |
∫ |
dx |
|
|
|
|
|||||||||||
|
0 |
|
|
3 |
|
|
|
3 |
−x2 |
|
|
|
|
|
|||
|
|
|
− |
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
4 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
63 29 |
|
14x−x2 |
|
x |
2 |
+ y |
2 |
|
||||||||
11. |
∫ |
|
dx |
∫ |
|
|
|
f |
|
|
dy . |
||||||
|
0 |
|
|
3− |
9−x |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2a |
|
4ax−x2 |
|
|
|
|
|
|
|
|
4a |
|||||
12. |
∫ dx |
|
∫ |
|
|
f |
|
(x2 + y2 )dy + ∫ dx |
|||||||||
4ax−x2 |
f (x2 + y2 )dy . |
∫ |
0 |
2ax−x |
2 |
2a |
0 |
|
|
|
|
Вычислить двойные интегралы:
13. ∫∫(2x − y)dxdy , где G – треугольник с вершинами А(1,2), В(3,2), С(0,1)
G
14. ∫∫(3x +2 y)dxdy , где G – часть плоскости, ограниченная кривыми
G
y = x2/2 и y =  2x .
2x .
15. ∫∫xy dxdy , где G – часть плоскости, ограниченная кривыми
G
x2 + y2 = ax, x2+ y2 = 2ax и y = 0, y ≥ 0, a ≥ 0.
16. ∫∫2x2 y dxdy, где G – часть плоскости, ограниченная линиями
G
y 2 = ax, x2 + y2 = 2ax, y = 0, y > 0, a > 0.
Перейти к полярным координатам и вычислить интегралы:
17. ∫∫ex2 + y2 dxdy, G – кольцо, ограниченное концентрическими окруж-
G
ностями: x2 + y2 = 1 и x2+ y2 = 4.
45
