
integral
.pdf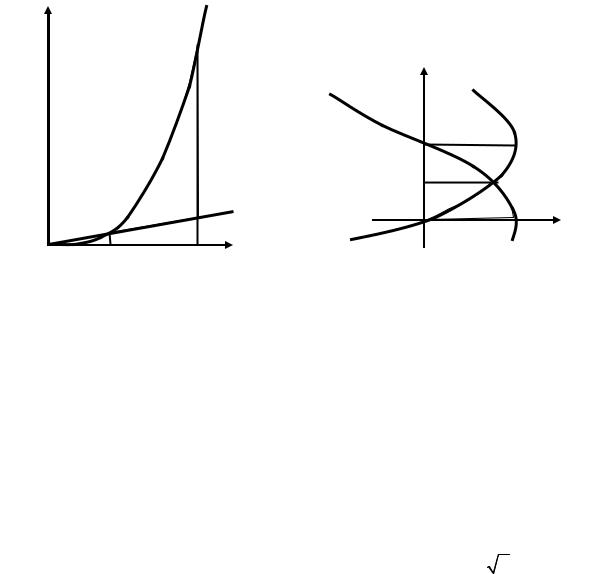
3 |
|
|
x7 |
|
x3 |
|
1504 |
|
|
∫ |
x5 |
− x3 + |
|
− |
|
dx = |
|
. |
|
2 |
2 |
3 |
|||||||
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Это и есть искомый повторный интеграл.
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = sin y |
|||||
|
|
|
|
y = x |
|
|
|
π/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
π/ 4 |
|
|
|
|
|
|
|
|
|
|
x = cos y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
3 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6. К примеру 1. |
|
|
|
Рис.7. К примеру 2. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
π / 4 |
|
cos y |
(x + y)dx . |
|||||||||
ПРИМЕР 2. Вычислить повторный интеграл ∫ |
dy ∫ |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
sin y |
|
|
|
|
|
|
|
|
|
|||
Имеем (см. рис.7): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
π / 4 |
cos y |
|
|
π / 4 |
|
x2 |
|
|
cos y |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫ dy ∫ |
(x + y)dx = ∫ |
dy |
|
+ y x |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
sin y |
|
|
0 |
|
|
|
|
sin y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
π / 4 cos2 |
y −sin2 |
y |
|
|
|
|
|
|
|
|
|
π |
2 |
|
|
3 |
|
||||
|
= ∫ |
|
|
|
|
+ y (cos y −sin y) dy |
= |
|
|
|
− |
|
|
. |
||||||||
|
|
2 |
|
|
|
4 |
4 |
|||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теперь осталось выяснить вопрос о том, как связаны повторные интегра-
лы (2) и (3) по переменным x и y, взятые в том или ином порядке, с введенным выше двойным интегралом по соответствующей области. Эта зависимость устанавливается следующими теоремами:
16

Теорема 1. Пусть правильная область D (первого типа) ограничена ли-
ниями x = a, x = b, y = φ1(х), у= φ2(х), где функции φ1, φ2 непрерывны на от-
резке [a, b] и φ1(х) ≤ φ2(х), а функция f (x, y) |
|
|
об- |
|||
непрерывна на замыкании D |
||||||
ласти D. Тогда двойной интеграл от этой функции по области D совпадает с |
||||||
повторным: |
|
|
|
|
|
|
|
b |
ϕ2 |
(x) |
|
|
|
∫∫ f (x, y)dxdy = ∫dx |
∫ f (x, y)dy, |
(4) |
|
|||
D |
a |
ϕ1 |
(x) |
|
|
|
Доказательство теоремы основано на трех леммах.
Лемма 1. Пусть a < c < b. Тогда:
b |
ϕ2 |
( x) |
c |
ϕ2 |
( x) |
b |
ϕ2 |
( x) |
∫dx |
∫ |
f (x, y) dy = ∫dx |
∫ |
f (x, y) dy + ∫dx |
∫ f (x, y) dy . (5) |
|||
a |
ϕ1 ( x) |
a |
ϕ1( x) |
c |
ϕ1( x) |
|||
Эта лемма представляет собой следствие свойства определенного инте-
грала от функции F(x), определенной равенством (1).
Лемма 2. Пусть функции φ1, φ2 и ψ непрерывны на отрезке [a, b], при-
чем φ1(х) ≤ ψ(х) ≤ φ2(х), и пусть функция f (x, y) непрерывна на D . Тогда
b ϕ2 ( x) |
b ψ ( x) |
b ϕ2 ( x) |
|||
∫dx |
∫ |
f (x, y)dy = ∫dx |
∫ f (x, y)dy + ∫dx |
∫ f (x, y)dy . (6) |
|
a ϕ1 ( x) |
a ϕ1( x) |
a ψ ( x) |
|||
Чтобы доказать это утверждение, зададим для любого фиксированного x |
|||||
некоторую первообразную Φ(x, y) |
функции f (x, y) . |
По формуле Ньютона − |
|||
Лейбница при фиксированном x получаем: |
|
|
|||
h( x) |
f (x, y)dy = Φ(x,h(x)) −Φ(x, g(x)) . |
|
|
||
∫ |
|
(7) |
|||
g( x)
Примéним формулу (7) отдельно к левой и правой частям формулы (6). Тогда получим
17
левая часть (6) =
b |
|
|
|
|
b |
b |
= ∫dx(Φ(x,ϕ2 (x)) −Φ(x,ϕ1(x))) = ∫Φ(x,ϕ2 (x))dx −∫Φ(x,ϕ1(x))dx ; |
||||||
a |
|
|
|
|
a |
a |
правая часть (6) = |
|
|
||||
b |
|
|
|
|
b |
|
= ∫dx(Φ(x,ψ (x)) −Φ(x,ϕ1(x))) + ∫dx(Φ(x,ϕ2 (x)) −Φ(x,ψ (x))) = |
||||||
a |
|
|
|
|
a |
|
b |
|
|
|
b |
b |
b |
= ∫Φ(x,ψ (x))dx −∫Φ(x,ϕ1(x))dx + ∫Φ(x,ϕ2 (x))dx −∫Φ(x,ψ (x))dx = |
||||||
a |
|
|
|
a |
a |
a |
|
|
|
|
|
|
= левой части (6). |
Лемма 3. (Теорема о среднем для повторного интеграла). Суще- |
||||||
ствует точка (x, y) |
|
такая, что: |
|
|||
D |
|
|||||
b |
ϕ2 |
( x) |
f (x, y)dy =f (x, y) | D | , |
|
||
ID = ∫dx |
∫ |
|
||||
a |
ϕ1( x) |
|
|
|||
где |D| − площадь области D.
Доказательство этого утверждения дословно повторяет доказательство теоремы о среднем для двойного интеграла (свойство 5).
Теперь можно доказать теорему 1.
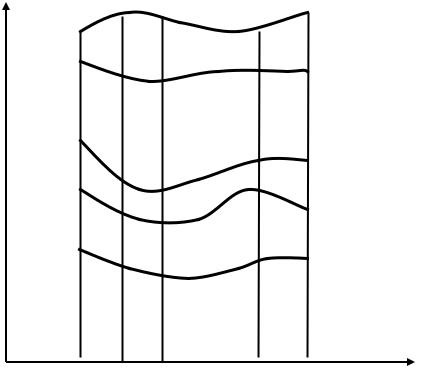
Доказательство теоремы 1. Разобьем область D на подобласти Di
прямыми, параллельными оси Оу: х = сq, (q = 1, 2, …, A+1), где а = c1 < c2 <…<
<cA < cA+1 = b, и кривыми: y = ψj(x), ( j = 1, 2, …, k +1), где φ1(x) = ψ1(x) < ψ2(x) <
<…< ψk(x) < ψk+1(x) = φ2(x) (рис. 8). В результате область D оказывается раз-
битой на n, (n = A k), криволинейных трапеций с основаниями, параллельными
оси Оу.
18
Y |
|
|
y=ϕ2 (x) =ψk +1 (x) |
|
… |
Dn |
|
||
|
|
y=ψk (x) |
||
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
y=ψ2 (x) |
|
|
|
||
|
D1 D2 |
|
|
y=ψ1 (x) |
|
… |
|
y=ϕ1 (x) =ψo(x) |
|
|
|
|||
|
|
|
|
|
a=c |
o |
c |
1 |
c2 |
… |
c |
cA+1=b |
X |
|
|
|
|
A |
Рис.8. К доказательству теоремы 1.
Из лемм 1 и 2 следует, что повторный интеграл по области D будет равен сумме повторных интегралов:
n |
|
A |
k |
cq+1 |
ψ j+1( x) |
|
|
||||
ID = ∑ID |
= ∑ ∑ |
∫ dx ∫ f (x, y) dy . |
|
|
|||||||
i=1 |
i |
q=1 j=1 c |
ψ |
|
|
( x) |
|
|
|||
|
j |
|
|
||||||||
|
|
|
|
q |
|
|
|
|
|
||
По лемме 3 существует точка (xi , yi ) |
|
i такая, что ID |
= f (xi , yi ) | Di | . Сле- |
||||||||
D |
|||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
довательно, |
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
ID = ∑ID |
= ∑ f (xi , yi ) | Di | = ST . |
|
(8) |
||||||||
i=1 |
i |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В правой части выражения (8) стоит интегральная сумма ST |
для двойного |
||||||||||
интеграла ∫∫ f (x, y)dxdy . |
Следовательно, при неограниченном |
уменьшении |
|||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
частей Di, в пределе получим
19
lim |
ST = ∫∫ f (x, y)dxdy . |
dT →0 |
D |
Но выражение под знаком предела есть постоянная, равная ID , а значит,
∫∫ f (x, y)dxdy = |
|
|
b |
ϕ2 |
( x) |
lim S |
T |
= ID = ∫dx |
∫ f (x, y)dy . |
||
D |
dT →0 |
a |
ϕ1( x) |
||
Теорема доказана.
Приведем также геометрическое доказательство того же утверждения для случая f (x,y) ≥ 0. Как было показано выше, для этого случая двойной интеграл
∫∫ f (x, y)dxdy равен объему криволинейного цилиндра U, изображенного на
D
рис. 2 и рис. 9. С другой стороны, если обозначить через S(хо) площадь сечения тела U плоскостью х = хо = const, то, как известно из свойств определенного интеграла, объем тела можно найти интегрированием:
b
V = ∫S(x)dx .
a
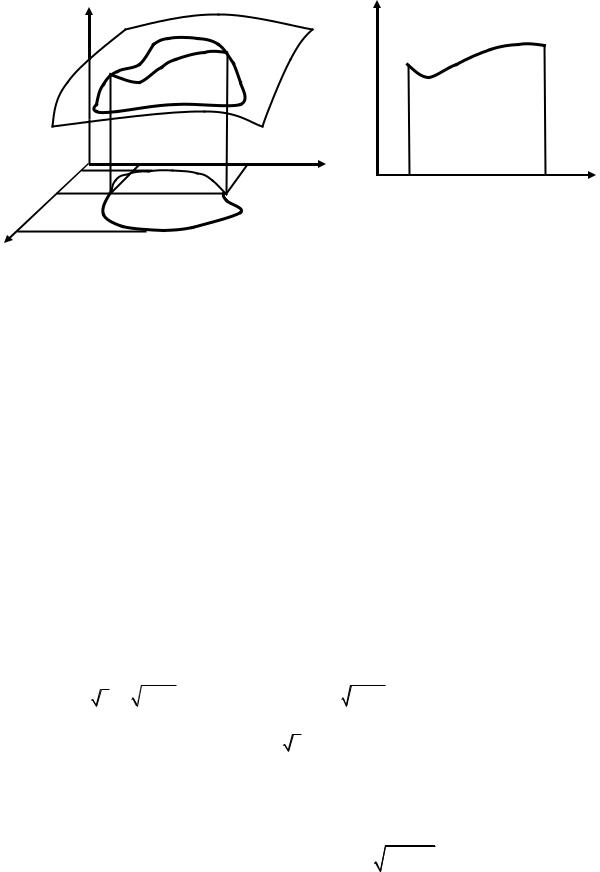
Рассмотрим сечение тела U плоскостью х = хо (рис. 9). Это сечение огра-
ничено отрезками АВ и СD, параллельными оси Оz, отрезком АС, параллель-
ным оси Оy и кривой ВD с уравнением z = f (хо,y), (точки А и С имеют, соот-
ветственно, координаты: А(хо, φ1(хо)), С(хо, φ2(хо)) в плоскости ОХY ). Пло-
щадь сечения вычисляется по формуле
ϕ2 |
(xo ) |
|
|
|
S(xo ) = |
∫ f (xo , y)dy . |
|
|
|
ϕ1 |
(xo ) |
|
|
|
Следовательно, |
|
|
|
|
|
b |
b |
ϕ2 |
( x) |
∫∫ f (x, y)dxdy =|U | = ∫S(x)dx =∫dx |
∫ f (x, y)dy . |
|||
D |
a |
a |
ϕ1( x) |
|
Теорема доказана.
20
|
Z |
|
Z |
z = f (xo,y) |
D |
|
|
D |
|
||||
|
|
B |
|
|||
|
B |
|
|
|||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
S(xo) |
|
|
|
a |
ϕ2 (xo ) Y |
A |
|
С |
|
|
0 |
|
||||
|
xo |
|
ϕ1(xo ) |
ϕ2 (xo ) Y |
||
b |
A |
C |
||||
|
|
|
||||
|
|
|
|
|
||
X
Рис.9. К выводу формулы для двойного интеграла: а)сечение тела U плоскостью; б)площадь сечения.
Аналогично формулируется и соответствующая теорема для случая правильной области второго типа:
Теорема 2. Для правильной области второго типа D′ (рис. 5) при огра-
ничениях, аналогичных сформулированным в теореме 1, двойной интеграл совпадает с повторным:
|
|
d ψ2 ( x) |
|
|
|
∫∫ f (x, y)dxdy = ∫dx ∫ f (x, y)dy . |
|
(9) |
|||
D′ |
|
c ψ1( x) |
|
|
|
ПРИМЕР 3. Изменить порядок интегрирования в интеграле: |
|||||
− 3 |
4−x2 |
0 |
2− 4−x2 |
|
|
I = ∫ dx ∫ |
f (x, y)dy + ∫ dx |
∫ |
f (x, y)dy . |
||
−2 |
0 |
− |
3 |
0 |
|
В данном интеграле область интегрирования D − правильная область первого типа (рис.10). По теореме 1 интеграл I записывается в виде двойного
интеграла: I = ∫∫ f (x, y)dxdy . Равенство y = 2 − 4 − x2 означает, что точка
D
21
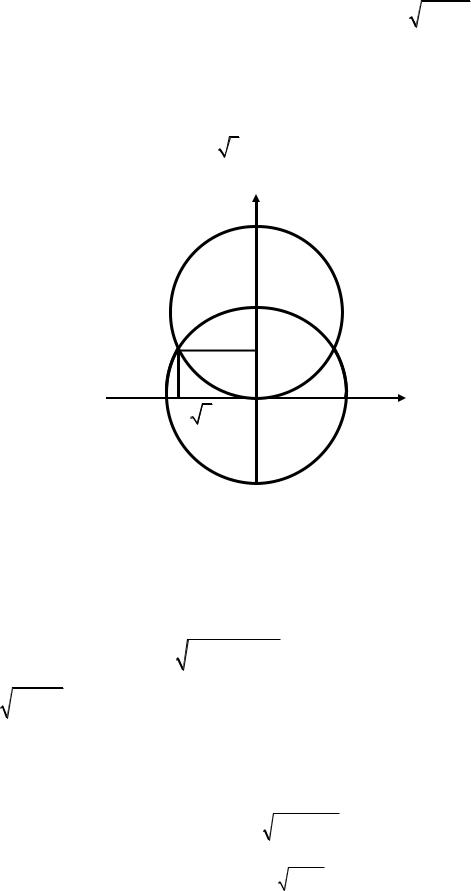
(х, у) лежит на окружности x2 +( y −2)2 = 4 . Если y = 4 − x2 , то точка (х, у)
лежит на окружности x2 + y2 = 4 . Две эти окружности пересекаются в точках,
для которых ( y −2)2 = y2 , или при у = 1. Подставляя это значение у в уравнение x2 + y2 = 4 , получаем x = ± 3 .
Y 4
x2 + ( y − 2)2 = 4
2
D |
1 |
x2+y2 |
= 4 |
|
|||
|
|
|
|
– 2 − 3 |
|
2 |
X |
Рис.10. К примеру 3.
Для обоих интегралов переменная х принимает только отрицатель-
ные значения. Значит для точек (х, у), лежащих на первой окружности, спра-
ведливо равенство x = − 4 −( y − 2)2 , а для точек второй окружности
x = − 4 − y2 .
Теперь, если рассмотреть область интегрирования D как правильную об-
ласть второго типа, то согласно теореме 2 интеграл I записывается в виде
|
1 |
− 4−(y−2)2 |
|
I = ∫∫ f (x, y)dx = ∫dy |
∫ |
f (x, y)dx . |
|
D |
0 |
− 4−y2 |
|
22
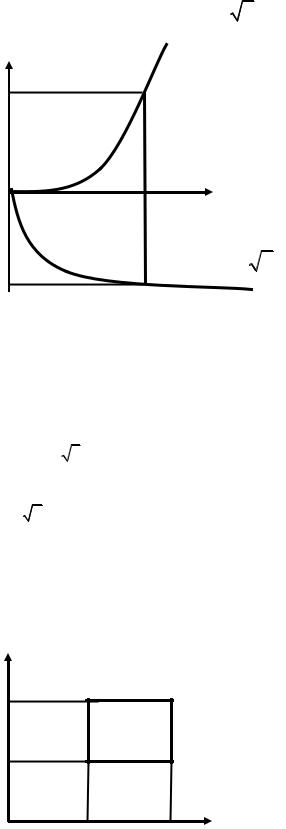
ПРИМЕР 4. Вычислить двойной интеграл: ∫∫(54x2 y2 +150x4 y4 )dxdy ,
где область D ограничена кривыми х = 1, y = x3, |
D |
||
|
y = − x (рис.11). |
||
|
|
|
|
Y |
|
y = x3 |
|
1 |
|
|
|
|
|
|
|
0 |
1 |
X
y = − x
– 1
Рис.11. К примеру 4.
Записывая двойной интеграл через повторный, получим
∫∫(54x2 y2 |
|
1 |
|
x3 |
(54x2 y2 +150x4 y4 )dy = |
+150x4 y4 )dxdy = ∫dx ∫ |
|||||
D |
|
0 |
|
− |
x |
1 |
|
3 |
|
1 |
(18(x11 + x7 / 2 )+30(x19 + x13 / 2 ))dx =11. |
= ∫dx (18x2 y3 +30x4 y5 ) |
−x |
x |
= ∫ |
||
0 |
|
0 |
|||
|
|
|
|
||
ПРИМЕР 5. Вычислить двойной интеграл ∫∫12 ye6xydxdy , где область D
D
ограничена прямыми: y = ln 3, y = ln 4, x = 1/6, x = 1/3 (рис.12).
Y
ln 4
D
ln 3
X
1/6 1/3
Рис.12. К примеру 5.
23
Рассматривая область D как правильную область 2-го типа, получим
∫∫12 ye6xydxdy = |
ln 4 |
1/ 3 |
|
|
|
|
|
|
∫ |
dy ∫ 12 ye6xydx = |
|
|
|
|
|
||
D |
ln 3 |
1/ 6 |
|
|
|
|
|
|
ln 4 |
1/ 3 |
ln 4 |
ydy e |
6xy |
|
1/ 3 |
ln 4 |
(e2 y −ey )dy = 5. |
|
||||||||
=12 ∫ ydy ∫ |
e6xydx =12 ∫ |
|
|
= 2 ∫ |
||||
ln 3 |
1/ 6 |
ln 3 |
6 y |
|
1/ 6 |
ln 3 |
|
|
|
|
|
|
|
||||
Этот же двойной интеграл можно найти и при помощи повторного инте- |
||||||||
|
|
|
|
|
1/ 3 |
ln 4 |
|
|
грала (9) с обратным порядком интегрирования |
|
∫ dx ∫ 12e6xy ydy , т.е. считая |
||||||
|
|
|
|
|
1/ 6 |
ln 3 |
|
|
D областью 1-го типа, но в этом случае сложность преобразований значительно выше.
Замечание. Обычно, при вычислении двойных интегралов, предварительно оценивают трудоемкость интегрирования подынтегральной функции по переменным x и y, взятым в том или ином порядке. В зависимости от результата такого анализа, область интегрирования нужно записать либо как правильную область первого типа, либо как правильную область второго типа. Иногда для этого приходится разбивать область на несколько правильных частей.
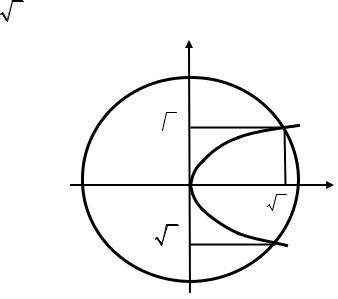
ПРИМЕР 6. Найти площадь области, ограниченной линиями x2 + y2 =12 , x 6 = y2 , х ≥ 0 (рис.13).
Y
x2+ y2=12
 6
6
X
0 |
6 |
− 6
Рис.13. К примеру 6.
24

По свойству 1 двойного интеграла площадь области D равна
| D |= ∫∫dxdy = |
6 |
12−y2 |
6 |
|
12 − y |
2 |
− y |
2 |
/ |
6 |
|
|
|||
∫ |
dy |
∫ |
dx = |
∫ |
|
|
|
dy = 3π + 2. |
|||||||
D |
− |
6 |
y2 / |
6 |
− 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ПРИМЕР 7. Найти объем тела, ограниченного поверхностями z + y = 1/2, |
|||||||||||||||
z = 0, x =17 2 y, |
x = 2 |
2 y |
(рис.14). |
|
|
|
|
|
|
|
|
|
|
||
Заданное тело представляет собой криволинейный цилиндр с образующей,
параллельной оси ОZ. Направляющей цилиндрической поверхности служат две ветви (при х > 0) парабол x =17 2 y и x = 2 2 y . Нижним основанием тела служит плоскость ОХУ, а сверху оно ограничено плоскостью z + y = 1/2.
|
z + y = 1/2 |
X |
Z |
|
1/2 |
|
17 |
|
0 |
x = 17 2 y |
x = 2 2 y |
|
1/2
Y
Рис.14. К примеру 7.
Как отмечалось выше в п. 4.1 объем такого криволинейного цилиндра выражается через двойной интеграл (рис. 14):
V = ∫∫(1/ 2 − y)dxdy = |
1/ 2 |
17 |
2 y |
1/ 2 |
|
∫ |
dy |
∫ |
(1/ 2 − y)dx = ∫ |
(1/ 2 − y) 15 2 y dy =1. |
|
D |
0 |
2 |
2 y |
0 |
|
25
