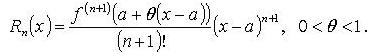export
.pdfОпределения
1
Производной функции f(x) в точке 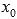 называется предел отношения приращения функции к приращению аргумента при
называется предел отношения приращения функции к приращению аргумента при 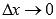 . Обозначается
. Обозначается 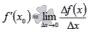 .
.
2
Уравнение касательной и нормали к графику функции y(x) в точке (x0 ; y0):
(yy0)=k*(xx0) касательная;
(yy0)=(1/k) * (xx0) нормаль, где k=y'(x0)
Касательная прямая прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.
3
Пусть функция y = f(x) определена в некоторой окрестности точки x0.
Функция f(x) называется дифференцируемой в точке х0, если ее приращение представимо в виде
Δf = f(x0 + Δx) − f(x0) = A ∙ Δx + o(Δx) ,
где A — число, не зависящее от х, а o(Δx) — функция более высокого порядка малости чем Δx при х → 0 .
Таким образом, приращение дифференцируемой функции является суммой линейной относительно Δx ч асти A ∙ Δx и бесконечно малой более высокого порядка малости чем Δx при х → 0.
Линейная часть приращения дифференцируемой функции называется дифференциалом в точке х0 и обозначается символом df(x0), т.е.
df(x0) = A ∙ Δx.
4
Бесконечая производная функции.
Операция нахождения производной функции называется дифференцированием этой функции. Функция 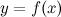 имеет производную на интервале
имеет производную на интервале 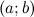 или называется дифференцируемой в этом интервале, если производная
или называется дифференцируемой в этом интервале, если производная 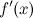 существует в каждой точке этого интервала.
существует в каждой точке этого интервала.
Функция 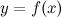 имеет в точке
имеет в точке  бесконечную производную, если в этой точке
бесконечную производную, если в этой точке
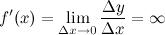 .
.
Определение:
Правой производной 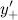 функции
функции 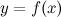 в данной точке
в данной точке 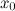 называется величина:
называется величина:
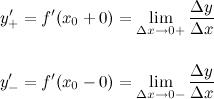
а левой производной величина:
если эти пределы существуют.
5
Производной nго порядка (nой производной) от функции f (x) (n>1) называется производная первого порядка от производной (n1) порядка функции f (x) при условии, что она существует.
f(n)(x) = (f(n1)(x))' , nЄR
6
Дифференциалом функции называется линейная относительно 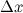 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 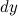 или
или 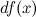 . Таким образом:
. Таким образом: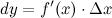
7
Дифференциал dy функции y=f(x) в некоторой точке x назовем первым дифференциалом функции в данной
точке.
Дифференциалом второго порядка функции y=f(x) в некоторой точке называют дифференциал в этой точке от дифференциала первого порядка в данной точке.
Очевидно, что дифференциалом третьего порядка называют дифференциал(если он существует) от дифференциала второго порядка.
Вообще дифференциалом nго порядка функции y=f(x) в некоторой точке называют дифференциал в этой точке( если он существует) от дифференциала (n1)го порядка в указанной точке.

8
Пусть функция f(x) определена в некоторой окрестности точки x0 и n раз дифференцируема в точке x0.
Многочлен 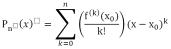 называется многочленом Тейлора n–го порядка функции f(x) с центром в точке x0 .
называется многочленом Тейлора n–го порядка функции f(x) с центром в точке x0 .
9
Рассмотрим многочлен 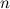 й степени
й степени
Его можно представить в виде суммы степеней  , взятых с некоторыми коэффициентами. Продифференцируем его
, взятых с некоторыми коэффициентами. Продифференцируем его 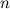 раз по переменной
раз по переменной  , а затем найдем значения многочлена и его производных в точке
, а затем найдем значения многочлена и его производных в точке 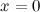 :
:
Таким образом, получаем, что
Полученное выражение называется формулой Маклорена для многочлена 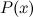 степени
степени 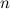 .
.
10
Функция возрастает на интервале, если для любых двух точек этого интервала, связанных отношением
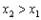 , справедливо неравенство
, справедливо неравенство 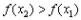 . То есть, бОльшему значению аргумента соответствует бОльшее значение функции, и её график идёт «снизу вверх». Демонстрационная функция
. То есть, бОльшему значению аргумента соответствует бОльшее значение функции, и её график идёт «снизу вверх». Демонстрационная функция 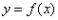 растёт на
растёт на
интервале 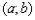 .
.
Аналогично, функция убывает на интервале, если для любых двух точек данного интервала, таких, что
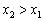 , справедливо неравенство
, справедливо неравенство 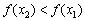 . То есть, бОльшему значению аргумента соответствует мЕньшее значение функции, и её график идёт «сверху вниз». Наша функция
. То есть, бОльшему значению аргумента соответствует мЕньшее значение функции, и её график идёт «сверху вниз». Наша функция 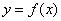 убывает на интервалах
убывает на интервалах 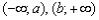 .
.
11
Точка 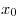 называется точкой максимума [точкой минимума] функции
называется точкой максимума [точкой минимума] функции 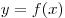 , если существует такая
, если существует такая 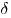 окрестность
окрестность 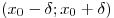 точки
точки 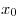 , что для всех значений
, что для всех значений 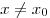 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 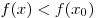
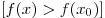 . Точки минимума и точки максимума называются точками экстремумафункции
. Точки минимума и точки максимума называются точками экстремумафункции  , а значения функции в этих точках экстремумами функции
, а значения функции в этих точках экстремумами функции 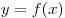 .
.
Стационарная точка функции 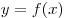 это точка, где f ’(x0)=0, либо f ’(x0) не существует.
это точка, где f ’(x0)=0, либо f ’(x0) не существует.
Критическая точка функции  называется точка, в которой все её частные производные обращаются в ноль.
называется точка, в которой все её частные производные обращаются в ноль.
12
Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
13.
Точка перегиба графика функции.
Точка графика, в которой он меняет выпуклость на вогнутость или вогнутость на выпуклость, называется точкой перегиба.
Теоремы
1
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
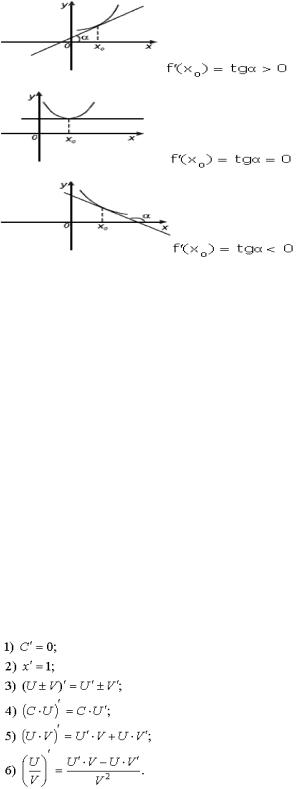
Уравнение касательной и нормали к графику функции y(x) в точке (x0 ; y0): (yy0)=k*(xx0) касательная;
(yy0)=(1/k) * (xx0) нормаль, где k=y'(x0)
2
Связь дифференцируемости с существованием конечной производной и дифференцируемости
функции.
1)Для того чтобы функция y=f(x) имела в произвольной точке x0 конечную производную, необходимо и достаточно, чтобы она была дифференцируема в этой точке.
2)Если функция дифференцируема в точке, то она непрерывна в этой точке.
3
Основные правила дифференцирования
Пусть 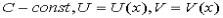 , тогда:
, тогда:
7) Если 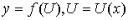 , то есть
, то есть 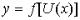 , где
, где 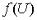 и
и 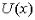 имеют производные, то
имеют производные, то 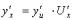 (правило дифференцирования сложной функции).
(правило дифференцирования сложной функции).
8) производная обратной функции: Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах 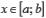 и
и  соответственно. Если в точке
соответственно. Если в точке 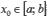 существует конечная отличная от нуля производная функции f(x), то в точке
существует конечная отличная от нуля производная функции f(x), то в точке 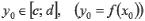 существует конечная производная обратной
существует конечная производная обратной
функции g(y), причем  . В другой записи
. В другой записи 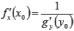
4
Односторонние производные
Выражение 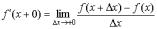 называется производной справа функции f(x) в точке x. Аналогично,
называется производной справа функции f(x) в точке x. Аналогично,
выражение 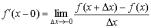 называется производной слева в этой же точке.
называется производной слева в этой же точке.
Если |
, то в точке x существует |
; если же |
, то в точке x |
производной |
не существует и график функции имеет излом; в этой точке имеется две касательных (см. |
||
рис) |
|
|
|
5
Механический смысл первой производной: скоростьэто производная координаты по времени, то есть v(t)=x’(t)
Механический смысл второй производной: ускорениеэто производная скорости по времени, то есть a=v’(t)
Иначе можно записать: a=x’’(t)
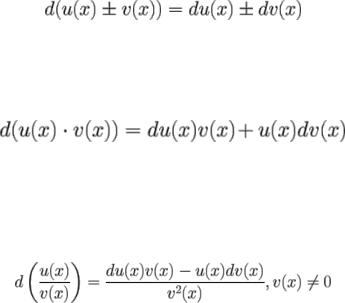
6
Правила вычисления дифферинциала
Дифференциал суммы/разности функций равен сумме/разности дифференциалов от каждого из слагаемых
Производная (дифференциал) произведения двух дифференцируемых функций равна сумме произведений производной (дифференциала) первого сомножителя на второй и производной (дифференциала) второго сомножителя на первый т.е.
Производная (дифференциал) дроби (частного двух дифференцируемых функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель представляет собой разность между произведением знаменателя данной дроби на производную (дифференциал) ее числителя и произведения числителя на производную (дифференциал) знаменателя.
7
Рассмотрим функцию y = f(u), где u = g(x), то есть рассмотрим сложную функцию y = f(g(x)). Если каждая из функций f и g являются дифференцируемыми, то производная сложной функции равна y' = f'(u)∙ u'. Тогда дифференциал функции
dy = f'(x)dx = f'(u)u'dx = f'(u)du,
так как u'dx = du. То есть
dy = f'(u)du.
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности
формы первого дифференциала.
8
Дифференциалы высших порядков.
Рассмотрим дифференциал функции  в произвольной точке промежутка
в произвольной точке промежутка  :
: 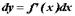 . Здесь
. Здесь
 приращение независимой переменной, которое является числом и не зависит от
приращение независимой переменной, которое является числом и не зависит от  . Сам же дифференциал есть функция от
. Сам же дифференциал есть функция от 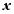 , и можно вычислить дифференциал от этой функции:
, и можно вычислить дифференциал от этой функции: 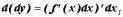 При
При 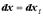 этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле
этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле 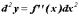 Аналогично вычисляется дифференциал любого порядка
Аналогично вычисляется дифференциал любого порядка  .
.
9
(Необходимое условие экстремума)
Теорема Ферма: Пусть функция f(х) определена на промежутке I и в некоторой внутренней точке х0 этого промежутка принимает наибольшее или наименьшее значение на этом промежутке. Тогда, если существует производная f’(x0), то эта производная равна нулю. Необходимое условие экстремума: во всех точках экстремума производная функции не существует или равна нулю.
10
Ролля теорема
Если функция f (х) непрерывна на отрезке а ≤ х ≤ b, имеет внутри его определённую производную, а на концах принимает равные значения f (a) = f (b), то её производная f'(x) по меньшей мере один раз обратится в нуль в интервале (a, b),
т. е. существует такое с (где a < с < b), что f’(с) = 0.
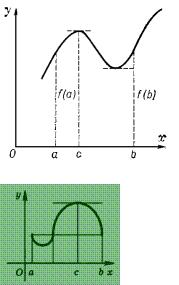
Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс
Теорема Лагранжа.
Если функция у = f (х) непрерывна на отрезке [а ; b] и дифференцируема в интервале (а ; b), то в этом
интервале найдется такая точка с, что 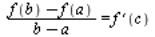
Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х) между точками А и В

найдется такая внутренняя точка С, что касательная к графику в точке С 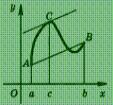 параллельна хорде
параллельна хорде
АВ.
Теорема Коши.
Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];
2)дифференцируемы в интервале (а ; b);
3)g'(x) ≠ 0 в этом интервале,
то в интервале (а ; b) существует такая точка с, что имеет место равенство
11
Правило ЛопиталяБернулли раскрытия неопределенности вида 0/0, беск/беск.
Как в случае неопределенности типа 0/0, т. е. когда
так и в случае 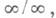 т. е. когда
т. е. когда
раскрытые неопределнности вида: 1) 0* беск
нужно преобразовать к виду f(x)/(1/g(x)), т.е к виду 0/0, либо к виду g(x)/(1/f(x)), т.е к виду беск на беск. 2)беск беск
нужно преобразовать к виду f(x) * (1g(x)/f(x)), затем раскрыть по беск/беск по правилу лопиталя.

3) 0 в степени 0, беск в степени 0, 1 в степени бесконечность
y=f(x)^g(x), логрифмируем. получаем lny=g(x)*ln(f(x)). во всех трех случаях lny является неопределенностью типа 0*бескб которы мы рассматривали раннее.
12
Сравнение роста показательной, степенной и логарифмической функций в бесконечности.
Теорема. Пусть 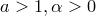 . Тогда
. Тогда
1) 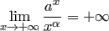 ;
;
2) 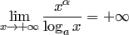 .
.
Лемма 1. Следующие утверждения эквивалентны
Замечание. Если одно из этих утверждений выполняется для любых 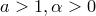 , то и два других справедлинвы
, то и два других справедлинвы 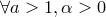 .
.
13
Свойства многочлена Тейлора.
Теорема: (основное свойство многочлена Тейлора) Пусть функция y=f(x) – n – раз дифференцируема в точке х0 f(x)=Tn(x0); f’(x0)=Tn’(x0),…,f(n)(x0)=Tn(n)(x0)
14
Формула Тейлора nго порядка с остаточным членом в форме Пеано:
Если функция y= f(x) определена и n раз дифференцируема в 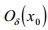 , то при имеет место формула:
, то при имеет место формула:
,
В форме Лагранжа: