export

15

Формула Маклорена с остаточным членом в форме Пеано имеет вид:

Для разложения по формуле данных функций можно воспользоваться готовыми разложениями 1)

16

Достаточное условие монотонности дифференцируемой функции.

Пусть функция y=f(x) определена и диффиренцируема на промежутке( a,b)

Тогда:1) если x (a ,b) f′(x) >0, то f(x) монотонно возрастает на промежутке (a,b)

2) если x (a,b) f′(x) <0, то f(x) монотонно убывает на промежутке(a,b)

17

(Необходимое условие экстремума)

Если функция 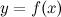имеет экстремум в точке 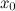, то ее производная 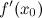либо равна нулю, либо не существует.

(Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1.функция непрерывна в окрестности точки ;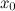

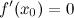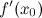2. или не существует;

3.производная 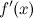при переходе через точку 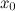меняет свой знак.

Тогда в точке 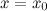функция 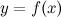имеет экстремум, причем это минимум, если при переходе через точку 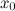производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку 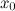производная меняет свой знак с плюса на минус.

(Второе достаточное условие экстремума)

Пусть для функции 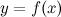выполнены следующие условия:

1.она непрерывна в окрестности точки ;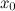

2.первая производная 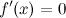в точке ;

3.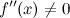 в точке .

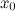Тогда в точке достигается экстремум, причем, если 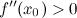, то в точке 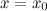функция 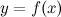имеет минимум; если 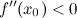, то в точке 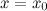функция 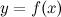достигает максимум.

18

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

если f '' ( x ) < 0 для любого x 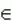( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b )

19

(О необходимом условии существования точки перегиба)

Если функция 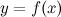имеет перегиб в точке 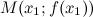, то 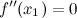или не существует.

(О достаточном условии существования точки перегиба)

Если:

1.первая производная 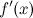неперрывна в окресности точки ;

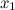2.вторая производная 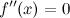или не существует в точке ;

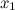3.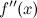 при переходе через точку меняет свой знак,

тогда в точке 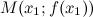функция 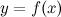имеет перегиб.

20

Схема полного исследования и построения графика функции.

1.Найти область определения функции.

2.Исследовать четность и периодичность функции.

3.Исследовать точки разрыва, найти вертикальные асимптоты.

4.Найти наклонные асимптоты (если их существование возможно).

5.Найти точки пересечения графика с осями координат.

6.Найти y’. Определить точки экстремума, интервалы возрастания и убывания функции.

7.Найти y’’. Определить точки перегиба графика, интервалы его выпуклости и вогнутости.

8.Построить график функции. Начертить асимптоты, отметить все точки, найденные в ходе исследования (пересечения с осями координат, максимума/минимума, перегиба).

Вопрос №1

Теорема Ферма: Пусть функция f(х) определена на промежутке I и в некоторой внутренней точке х0 этого

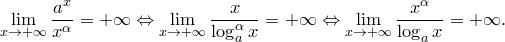
промежутка принимает наибольшее или наименьшее значение на этом промежутке. Тогда, если существует производная f’(x0), то эта производная равна нулю. Необходимое условие экстремума: во всех точках экстремума производная функции не существует или равна нулю.

Вопрос №2

Вопрос №3

Вопрос №4

Теорема. Пусть 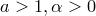. Тогда

1) ;

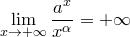2) .

ax ­ показательная xa ­ степенная

Лемма 1. Следующие утверждения эквивалентны

Замечание. Если одно из этих утверждений выполняется для любых 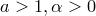, то и два других справедлинвы .

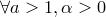Вопрос №5 Вопрос №6 Вопрос №7

Вопрос №8 Вопрос №9 Вопрос №10

(Необходимое условие экстремума)

Если функция 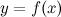имеет экстремум в точке 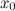, то ее производная либо равна нулю, либо не существует.

(Первое достаточное условие экстремума)

Пусть для функции 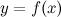выполнены следующие условия:

4.функция непрерывна в окрестности точки ;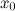

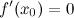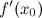5. или не существует;

6.производная при переходе через точку 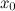меняет свой знак.

Тогда в точке 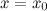функция 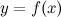имеет экстремум, причем это минимум, если при переходе через точку 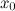производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку 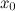производная меняет свой знак с плюса на минус.

(Второе достаточное условие экстремума)

Пусть для функции 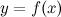выполнены следующие условия:

4.она непрерывна в окрестности точки ;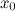

5.первая производная 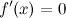в точке ;

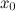6.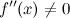 в точке .

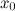Тогда в точке 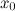достигается экстремум, причем, если , то в точке функция 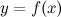имеет минимум; если 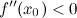, то в точке 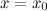функция 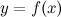достигает максимум.

Вопрос №11

Достаточное условие выпуклости, вогнутости графика функции: если функция f(x) является дважды дифференцируемой и ее вторая производная f ”(x) сохраняет знак при всех x(a;b), то график функции имеет постоянное направление выпуклости на этом интервале: при f ’’(x)<0 – выпуклость вверх, при f ’’(x)>0 – вогнутость (выпуклость вниз).

Необходимое условие точки перегиба: Точка Мо является т. перегиба ф­ии f(x),если f’’(x)=0 или f’’(x) . Достаточное условие точки перегиба: Пусть f(x) имеет вторую производную в т.x0 и не прерывна в окр. т.x0. Если f’’(x)=0 и при переходе через x0 2­ая производная меняет знак, то точка М(х0,f(x0)) является т.перегиба.

Св­во касательной к графику в т.перегиба: Пусть f(x) имеет в т.Мо касательную, хотя бы и вертикальную. Пусть f(x) имеет в окр.х0 2­ую производную. Если f ”(x) в т.х0 равна 0 или , и при переходе через х0 меняет знак, то Мо есть точка перегиба.

Вопрос №12 Схема полного исследования и построения графика функции.

1.Найти область определения функции.

2.Исследовать четность и периодичность функции.

3.Исследовать точки разрыва, найти вертикальные асимптоты.

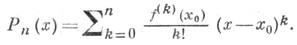
4.Найти наклонные асимптоты (если их существование возможно).

5.Найти точки пересечения графика с осями координат.

6.Найти y’. Определить точки экстремума, интервалы возрастания и убывания функции.

7.Найти y’’. Определить точки перегиба графика, интервалы его выпуклости и вогнутости.

8.Построить график функции. Начертить асимптоты, отметить все точки, найденные в ходе исследования (пересечения с осями координат, максимума/минимума, перегиба).

Вопрос №13

Многочлен, обладающий свойством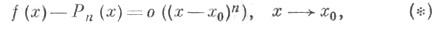, единствен. Где f(x) ­ функция а Pn(x) ­ многочлен тейлора.

Вопрос №14

Вопрос №15

Вопрос №16