
Формирование и передача сигнала_lekc
.pdfМинистерство транспорта Российской Федерации Федеральное государственное образовательное учреждение высшего профессионального образования
Волжская государственная академия водного транспорта
Кафедра информатики, систем управления и телекоммуникаций
А.В.Преображенский
ФОРМИРОВАНИЕ И ПЕРЕДАЧА СИГНАЛОВ. КОНСПЕКТ ЛЕКЦИй
Учебное пособие
Издательство ФГОУ ВПО ВГАВТ Н. Новгород, 2005
УДК 621.37 П 91
А.В. Преображенский. Формирование и передача сигналов. Конспект лекций. Учебное пособие. Н. Новгород: изд-во ФГОУ ВПО ВГАВТ, 2005.- 89 с.
Учебное пособие предназначено для студентов высших учебных заведений водного транспорта, обучающихся по специальности «техническая эксплуатация транспортного радиооборудования». Содержание пособия соответствует требованиям Государственного образовательного стандарта высшего профессионального образования.
Рассмотрены вопросы представления сигналов, генерации и усиления колебаний. Дано описание основ теории информации, принципов кодирования источника и канала, способов формирования широкополосных сигналов и построения многоканальных систем связи. Приведены примеры применения методов формирования сигналов в современных системах радионавигации и связи с подвижными объектами.
Рекомендовано к изданию кафедрой Информатики, систем управления и телекоммуникаций Волжской государственной академии водного транспорта 17. 12. 04, протокол № 4.
Рецензенты:
-кафедра Электроники и сетей ЭВМ Нижегородского государ-
ственного технического университета, зав. кафедрой академик МАИ проф. В.Г. Баранов и проф., д.т.н. В.Р. Милов,
-генеральный конструктор Нижегородского научноисследовательского института радиотехники, лауреат Государственных премий РФ доцент, к.т.н. А.А. Зачепицкий.
ФГОУ ВПО ВГАВТ, 2005.
1.Основные задачи формирования
ипередачи сигналов
Вданном курсе рассматриваются сигналы, используемые в радиотехнических системах и системах электросвязи. Радиотехнические системы по назначению разделяют на системы: передачи информации (радиосвязь, телеметрия, радио и телевещание), извлечения информации (РЛС, РНС, радиоастрономия, радио и радиотехническая разведка), разрушения информации, радиоуправления. Электросвязь - это системы звукового и телевизионного вещания, телефон, телеграф, передача документов (факс), радиовызов (пейджинг), электронная почта и т.д. Классификация систем достаточно условна: одна и та же система может выполнять разные функции, один и тот же канал связи используется одновременно разными системами.
Источник |
Кодер |
Кодер |
модулятор |
сообщения |
источника |
канала |
|
|
|
передатчик |
|
|
|
|
Линия |
|
|
|
связи |
Получатель |
Декодер |
Декодер |
демодулятор |
источника |
канала |
|
|
сообщения |
|
||
|
|
|
|
|
|
приемник |
|
|
система связи |
|
канал связи |
|
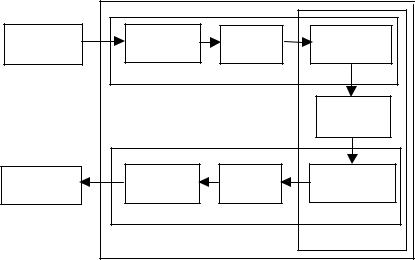
Рис.1 |
|
|
Основные классификационные признаки сигналов: периодичностьнепериодичность, непрерывность-дискретность, детерминированностьслучайность. По виду сигналов различают системы непрерывные, импульсные (с дискретизацией сигналов по времени) и цифровые (с дискретизацией сигналов по времени и квантованием по уровню).
Некоторые этапы формирования сигналов в цифровой системе передачи сообщений представлены на рис.1 Сообщение выдается источником в виде буквенно-цифрового текста или аналогового "первичного" сигнала (с микрофона, видеокамеры, датчика системы управления и т.д). Кодер источника форматирует сообщение, представляя в форме, необходимой для цифровой обработки: последовательностью двоичных знаков 0 и 1 (битов). Количество знаков 0 и 1 в этой последовательности может быть сокращено при рациональном кодировании, устраняющем "избыточность". То, что это возможно при текстовых сообщениях, следует хотя бы из того, что один и тот же текст на разных языках содержит разное количество знаков. При передаче сигналов звука и изображения широко применяются методы кодирования источника с предсказанием последующих значений сигнала по предыдущим и передачей вместо абсолютных значений сигнала ошибок его предсказания или, по крайней мере, изменений сигнала по отношению к предыдущим значениям.
В канале связи сигнал искажается под влиянием ряда факторов. Это собственный тепловой шум приемной аппаратуры, нелинейные и линейные искажения вследствие неидеальности характеристик элементов системы, атмосферные, индустриальные и даже преднамеренные помехи, замирания сигнала из-за многолучевого распространения и т.д. Искажения сигнала в цифровых системах приводят к ошибкам. Значительное число ошибок может быть обнаружено и даже исправлено применением корректирующих кодов. Кодер канала добавляет к "информационным" битам сообщения проверочные биты таким образом, чтобы из всех возможных кодовых комбинаций можно было выделить заведомо ошибочные и заменить их на "ближайшие" разрешенные, считающиеся "правильными". Помехоустойчивые коды применяются с учетом характера типовых ошибок в конкретной системе связи. В результате работы кодеров передатчика формируется последовательность двоичных знаков (0,1), представленных разными уровнями напряжения (или тока). Соответствующий сигнал является последовательностью однополярных или разнополярных импульсов (видеоимпульсов). Различные варианты такого представления называют кодами канала, кодированием "в основной полосе частот", "узкополосной модуляцией".
Сигнал с выхода кодера управляет одним или несколькими параметрами высокочастотного (ВЧ) колебания (амплитудой, частотой, фазой). Эта процедура называется модуляцией. В цифровых системах процесс модуляции часто называют манипуляцией. Способ модуляции выбирают таким образом, чтобы обеспечить наиболее достоверную передачу сообщения. Параметры ВЧ-колебания устанавливаются модулятором в зависимости от бита двоичной последовательности или "символа" - группы из

“к” бит. Эта группа содержит М=2к разных кодовых комбинаций, так что модулирумый параметр ВЧ-колебания может принимать М различных значений. Такой способ передачи сигналов, в отличие от двоичного (бинарного) называется М-арным, а скорость передачи измеряется в бодах - количестве переданных символов в единицу времени (секунду).
Демодулятор и декодеры выполняют преобразования сигнала, обратные модуляции и кодированию.
Схема рис.1 отражает только часть операций формирования сигналов. Для обеспечения конфиденциальности сообщений может потребоваться шифрование. В многоканальных системах после канального кодирования производится уплотнение - формирование группового сигнала из сигналов нескольких источников. Кодирование и модуляция могут выполняться в несколько этапов с использованием различных способов. В системе имеются средства для разрешения конфликтов различных пользователей при одновременном обращении к одному каналу и обеспечения взаимной синхронизации передатчика и приемника.
Основными требованиями к системам связи являются: высокая скорость передачи сообщений, измеряемая в бит/c или бодах, многоканальность, малая вероятность ошибки передачи бита или символа (в цифровых системах), защита от несанкционированного доступа, простая аппаратная реализация.
Принципиальные сложности при передаче сигналов: расширение спектра сигнала при увеличении скорости передачи сообщений и увеличение вероятности ошибки при уменьшении отношения сигналшум. Существует понятие объема (емкости) сигнала Vc= Tc Fc Нс, где Тс- время передачи сигнала, Fс- ширина спектра сигнала, Нс- превышение уровня сигнала над помехой. Объем (емкость) канала Vк выражается произведением аналогичных величин, характеризующих возможности канала. Сообщение можно успешно передать при условии Vc<Vk. В случае несоответствия отдельных параметров сигнала и канала может быть найден компромисс путем рационального выбора методов кодирования и модуляции.
Компромисс легче достигается в цифровых системах. У них выше помехоустойчивость, проще регенерация сигнала, возможно применение кодов, корректирующих ошибки. Нет проблем с длительным запоминанием сигнала. Благодаря высокой помехоустойчивости удается плотнее разместить каналы в полосе частот и, соответственно, полнее использовать пропускную способность физического канала. Аппаратная реализация цифровых устройств проще, чем аналоговых, выше степень интеграции микроэлектронных схем и унификация, а следовательно дешевле аппаратура. Есть возможность применения сложных алгоритмов обработки сигналов.
2. Основные характеристики сигналов
Для описания процессов формирования и передачи сигналов необходимы математические модели сигналов и элементов систем. Детерминированные сигналы описываются в двух основных формах: временной и частотной. В качестве моделей элементов систем используются дифференциальные и конечно-разностные уравнения в обычной и матричной формах, передаточные функции и характеристики: переходная h(t) и импульсная переходная g(t). Это реакции на единичный скачок 1(t) и короткий импульс, описываемый δ - функцией.
2.1. Временная форма представления сигнала
Математической моделью сигнала является функция времени s(t). При описании прохождения сигнала через линейный элемент используется импульсная переходная характеристика элемента g(t). Сигнал s(t) разделяется на короткие элементарные импульсы. На рис.2 для примера показаны отклики на 2 импульса. В результате суммирования откликов получается сигнал на выходе элемента. При бесконечно малой длительности элементарных импульсов суммирование сводится к интегрированию:
sвых (t) = ∫t |
s(t − τ )g(τ )dτ |
= ∫t |
s(τ , )g(t − τ , )dτ ,. |
(1) |
0 |
|
0 |
|
|
Выражение (1), записанное в двух вариантах выбора переменной интегрирования, называют интегралом наложения, сверткой функций s(t) и g(t), интегралом Дюамеля.
S(t-τ)=S(τ’)
0 |
t |
 g(τ) s(t-τ)
g(τ) s(t-τ)
τ’ τ
Рис.2
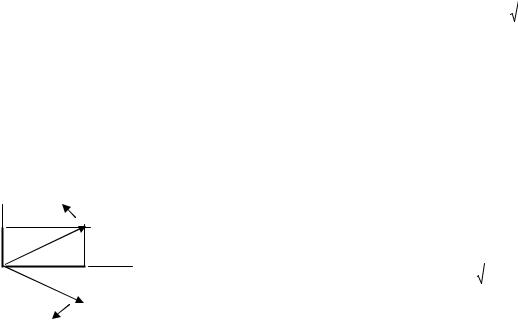
2.2. Частотная форма представления периодического сигнала
Периодический сигнал s(t) представляют в виде ряда Фурье - суммы гармонических составляющих. Такое представление удобно для линейных систем, поскольку в них справедлив принцип суперпозиции, реакция на гармоническое воздействие находится простым умножением входного сигнала, представленного в комплексной форме, на комплексный коэффициент передачи системы, а собственные движения системы являются гармоническими функциями.
Гармонический сигнал представляют в разных формах: Acosϕ(t) = Acos(ωt −ϕ0) = acosωt + bsinωt =
= |
A |
e |
− jϕ |
0 e |
jωt |
+ |
A |
e |
jϕ |
0 e |
− jωt |
, |
(2) |
|
|
|
|
|
|
22
называемых соответственно амплитудно-фазовой (A -амплитуда, |
ϕ(t) - |
||||
полная фаза, ϕ0 |
- начальная фаза), квадратурной |
и экспоненциальной |
|||
(комплексной). |
Последняя |
основана |
на |
формуле |
Эйлера |
e jϕ = cosϕ + j sinϕ и позволяет представить гармоническое колебание как сумму двух комплексно-сопряженных чисел, или вращающихся в противоположные стороны векторов (рис. 3). Вращение векторов в разные стороны описывается введением понятия отрицательной частоты. Мгновенная частота связана с полной фазой соотношением ω(t) = dϕ(t)/dt , так что отрицательная частота означает уменьшение фазы. Применение экспоненциальной формы упрощает математические преобразования гармонических сигналов.
e jϕ
sinϕ
cosϕ
e− jϕ
Рис.3
Ряд Фурье представляют в амплитудно-фазовой, тригонометрической и экспоненциальной формах:
|
2 |
|
|
∞ |
|
|
|
|
|
|
|
|
2 |
|
∞ |
|
|
|
|
|
|
|
|||
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|||||
s(t) = |
a |
0 |
+ |
|
A |
cos(nω |
t −ϕ |
|
) = |
|
a0 |
+ |
|
a |
|
cos nω |
t + b |
|
sin nω |
t = |
|||||
|
|
|
n |
|
|
|
|
n |
n |
||||||||||||||||
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|||
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
T / 2 |
|
|
|
|
|
|
|
|
|||
|
= ∑Cne jnω1t , |
|
Cn = |
1 |
|
|
∫s(t)e− jnω1tdt , |
|
|
(3) |
|||||||||||||||
|
|
T |
|
|
|
||||||||||||||||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
−T / 2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
T |
|
|
|
|
|
|
|
|
2 |
T |
|
|
|
|
|
|
|
|
||
a |
|
|
= |
|
|
∫ s(t) cos(nω t)dt; |
|
|
b = |
|
|
∫ s(t) sin(nω t)dt |
|
|
(4) |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
n |
|
|
T |
0 |
|
1 |
|
|
|
n |
|
|
T |
0 |
|
|
|
1 |
|
|
|
|
||
где ω1=2π/T - частота первой гармоники, Т и n - период и номер гармоники, ряд значений An и ϕn - спектры амплитуд и фаз, Cn - комплексные амплитуды, содержащие информацию и о спектре амплитуд, и о спектре фаз. В комплексном спектре спектр амплитуд |Cn| является четной функцией, спектр фаз – нечетной. Входящие в (3, 4 ) величины связаны между собой соотношениями
|
|
|
|
|
A |
= |
|
a2 |
+ b2 |
; |
ϕ |
n |
= arctg |
bn |
; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
n |
|
|
|
n |
|
n |
|
|
|
|
|
|
|
an |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
||||||
|
A |
|
|
|
a |
|
− jb |
|
A |
|
|
|
|
|
|
a |
|
+ jb |
|
a |
|||||||||
Cn = |
− jϕ |
|
= |
n |
C−n = |
|
|
|
jϕ |
|
= |
n |
C0 = |
0 |
|
||||||||||||||
n |
e |
|
n |
|
|
|
n |
; |
n |
|
e |
|
n |
|
|
|
n |
; |
|
. |
|||||||||
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В качестве примера найдем комплексный спектр последовательности прямоугольных импульсов с началом отсчета времени по фронту импульса (рис. 4а).
C |
n |
= |
|
1 |
|
T ∫/ 2 |
s(t)e− jnω1tdt = |
1 |
τ∫U |
0 |
e− jnω1tdt = − |
|
U0 |
|
(e− jnω1τ −1) = |
(6) |
||||||||||||||||||||||
|
|
|
|
jTnω |
||||||||||||||||||||||||||||||||||
|
|
|
T |
|
−T / 2 |
|
|
|
|
|
T |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||
− |
|
|
U0 |
|
|
|
(cosnω τ − jsin nω τ −1) = |
|
U0 |
[sin nω τ − j(1− cos nω τ )]. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
jTnω1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
nTω1 |
1 |
|
|
|
|
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
При τ=T/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
n |
= |
U0 |
|
[sinπn − j(1− cosπn)]. |
(7) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πn |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Согласно (7) спектры амплитуд Cn |
|
и фаз ϕn : |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
U0 |
|
|
|
|
|
= |
U0 |
|
sin π n |
|
, |
|
|
|||||||||||||||
|
|
|
|
C |
n |
|
= |
|
sin2 |
πn + (1− cosπn)2 |
|
|
|
(8) |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2πn |
|
|
|
|
|
|
|
|
|
|
|
|
πn |
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ϕn |
= arctg |
1− cosπn |
; |
tgϕn = |
1− cosπn |
= tg πn ; ϕn |
= πn . |
|
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sinπn |
|
|
|
|
sinπn |
|
|
|
|
|
2 |
|
2 |
|
|
|
|||||||||||
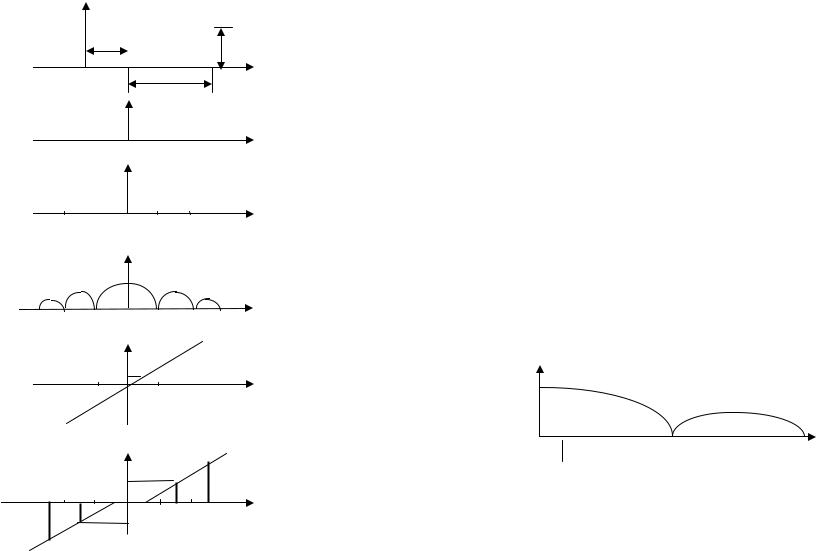
a) |
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
U0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) ReCn |
|
|
|
|
u0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 |
-2 0 |
2 |
|
|
4 |
|
||||||||||||||||
|
|
|
|
|||||||||||||||||||
в) JmCn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) |Cn| |
|
|
|
|
|
u0 |
|
|
|
u0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
π |
|
|
|
|
|
|
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д) ϕn |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e) ϕn |
π |
|
n
-π
Рис.4 (τ=T/2)
На рис. 4 показаны действительная и мнимая части комплексных коэффициентов Cn ряда (7) - (б, в), спектр амплитуд (г) и фаз (д).
Вид спектра фаз зависит от начала отсчета времени. При начале отсчета времени от середины импульса имеем
|
|
|
|
τ |
|
|
|
|
|
|
τ |
|
|
τ |
|
|
|
|
1 |
2 |
|
|
− jnω t |
U0 |
|
− jnω |
|
jnω |
|||
|
|
|
|
|
|
1 |
|
1 |
|||||||
C |
n |
= |
|
∫ U |
0 |
e |
1 dt = − |
|
(e |
|
2 |
− e |
|
2 ) = |
|
|
jnω T |
|
|
||||||||||||
|
|
T |
|
τ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
− |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπτ |
|
|
(9) |
|
|
|
|
|
πnτ |
|
|
τ |
|
sin |
|
|
|
|||
= |
U |
0 |
|
= |
U |
T |
|
||||||||
|
sin |
|
0 |
|
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
πn |
T |
|
T |
|
|
|
nπτ |
|
|
|||||
T
В данном случае функция s(t) четная и ее комплексный спектр чисто действительный. Соответствующий спектр фаз при τ = T/2, указывающий знак комплексной амплитуды, показан на рис. 4е.
Рис. 4 представляет "двусторонний" спектр амплитуд и фаз с использованием отрицательных частот. В "одностороннем" спектре рассматриваются только положительные частоты, при этом амплитуды спектральных составляющих увеличиваются в 2 раза. На рис. 5 представлен односторонний спектр амплитуд последовательности прямоугольных импульсов. Через амплитудно-фазовую форму спектра данный сигнал выражается следующим образом
|
[τ |
|
|
∞ |
sin |
nπτ |
|
|
|
|
|
|
2 |
T |
(10) |
||||||
|
|
|
|
|||||||
s(t) = U0 |
+ |
∑ |
|
|
cos |
n2π |
t]. |
|||
π |
|
|
|
|
||||||
|
T |
|
n=1 |
n |
|
|
T |
|||
An
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2π/T |
|
|
|
2π/τ |
|
|
|
|
4π/τ |
||
|
|
|
|
|
|
|
|
||||
|
|
|
Рис.5 |
|
|
|
|
|
|
||
Периодический сигнал предполагается имеющим бесконечную длительность, следовательно и бесконечную энергию. Поэтому его характеризуют не энергией, а средней за период мощностью, зависящей только от спектра амплитуд:
|
|
T / 2 |
|
|
∞ |
|
∞ |
|
|
|
|||
P = |
1 |
∫ |
s2 (t)dt = |
1 |
∑An2 |
= ∑ |
|
Cn |
|
2 . |
(11) |
||
|
|
||||||||||||
|
|
||||||||||||
|
T |
2 |
n= |
0 |
n= −∞ |
|
|
|
|||||
|
|
−T / 2 |
|
|
|
|
|
|
|
|
|
|
|
При этом предполагается, что сигнал представлен напряжением или током, действующим на сопротивлении в 1 Ом.
Спектр фаз не имеет значения в задачах, где рассматриваются только энергетические соотношения, но важен в процессах передачи информации.
2.3. Спектр непериодического сигнала. Преобразование Фурье.
Непериодический сигнал, имеющий конечную длительность Т, можно характеризовать его энергией, которая ограничена, поэтому такой сигнал называют иногда "энергетическим". Как видно из рис.5, при Т →∞ будет получен "сплошной" спектр одиночного импульса, в котором спектральные линии расположены бесконечно близко друг к другу. Такой спектр описывается непрерывной спектральной функцией S(ω), являющейся преобразованием Фурье сигнала s(t):
S(ω) = |
∞∫ s(t)e |
− jωt dt. |
(12) |
||
|
|
−∞ |
|
||
|
|
|
|
||
Обратное преобразование |
|
|
|
||
s(t) = |
1 |
∞∫ S(ω)e jωt dω. |
|
||
2π |
(13) |
||||
|
−∞ |
|
|||
|
|
|
|||
При конечной длительности Т непериодического сигнала интегрирование в (12) производится на интервале от -T/2 до T/2 , так что формулы
(3) и (12) отличаются только множителем и
S(ω) = TCn = Cn / f1, |
(14) |
где f1 - частота первой гармоники, равная частотному интервалу между соседними линиями спектра периодического сигнала. Следовательно, спектральная функция сигнала конечной длительности имеет тот же вид, что и огибающая линейчатого спектра периодического повторения этого сигнала.
Спектральную функцию S(ω), имеющую размерность [амплитуда/Гц], называют также плотностью амплитуд, спектральной плотностью, а иногда и просто спектром. Величина | S(ω)| 2 имеет физический смысл плотности энергии, т.е. энергии, приходящейся на полосу частот в 1 Гц, а полная энергия непериодического сигнала
|
T / 2 |
|
1 |
∞ |
|
2 |
1 |
∞ |
2 |
|
|||
E = |
2(t)dt = |
S(ω) |
|
dω = |
S(ω) |
|
dω. |
|
|||||
∫ s |
|
∫ |
|
|
∫ |
|
(15) |
||||||
|
|
||||||||||||
|
−T / 2 |
|
2π −∞ |
|
|
|
π |
0 |
|
|
|
|
|
Отметим некоторые выводы, следующие из преобразования Фурье. Спектральная функция δ -функции равномерна на всех частотах и
равна 1. Это следует непосредственно из определения (12).
Спектр выходного сигнала устройства является произведением спектра входного сигнала на комплексный коэффициент передачи устройства.
Т.к. спектральная функция δ - импульса равна 1, спектром импульсной переходной характеристики устройства является его комплексный коэффициент передачи.
s(t)
а) |
1 |
t
0
τ
S(f)
б)
τ 
 f 0
f 0
1/τ
S(f)
в)
f
-f1 |
0 |
f1 |
г) |
|
s(t) |
τ 
 t 0
t 0
1/2f1
Рис.6
Прямое и обратное преобразование Фурье (12) и (13) отличаются только множителем и знаком частоты в показателе экспоненты. При переходе от переменной ω к f множитель исчезает, а знак при ω не имеет значения для четных функций, у которых S(ω)=S(-ω) . Это означает, что переменные t и f в формулах (12) и (13), а следовательно и на графиках,
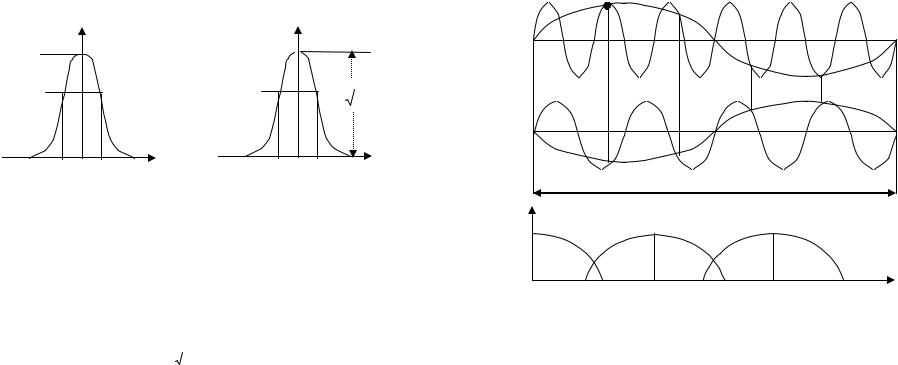
представляющих сигнал и его спектральную функцию, взаимозаменяемы. Если прямоугольный импульс (рис. 6а) имеет спектральную функцию вида sinx/x (рис.6б), то прямоугольный спектр рис.6в соответствует импульсу рис. 6г. Следовательно, короткий импульс, проходя через фильтр с частотной характеристикой рис. 6в, примет форму рис. 6г и не будет равен 0 даже при t→ - ∞. Невозможность появления отклика на импульс ранее прихода самого импульса означает неосуществимость фильтра с прямоугольной частотной характеристикой вида рис. 6 в.
При уменьшении длительности сигнала его спектр расширяется. Это видно, в частности, из приведенных выше примеров. Понятие ширины спектра достаточно условно, т.к. любой реальный сигнал имеет неограниченный спектр. Практическую, "эффективную" ширину спектра определяют разными способами, в частности, как полосу положительных частот, в которой сосредоточена основная доля энергии сигнала (например, 50%, 95%), или как ширину главного лепестка спектральной функции (при "многолепестковом" спектре).
|
|
s(t) |
|
|
|
|
|
S(ω) |
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
е-0,5 ≈0,606 |
|
|
|
|
|
|
|
|
60% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
2π |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-a |
0 |
a |
|
|
|
|
-1/a |
1/a |
|
|
|
||
|
|
|
|
|
Рис.7 |
|
|
|
|
|
|
||
Произведение длительности сигнала τ на ширину его односторонне- |
|||||||||||||
го спектра |
f |
называется базой сигнала. Независимо от способа опреде- |
|||||||||||
ления ширины спектра, при |
грубых |
оценках |
считается, |
что |
для ви- |
||||||||
деосигналов |
база |
|
|
|
|
|
|
|
|
|
|||
B = τ f ≈ 1. Например, для прямоугольного импульса f=1/ τ |
(ширина |
||||||||||||
главного лепестка АЧХ в области положительных частот) и |
В= 1. Мини- |
||||||||||||
мальной базой обладает "гауссов" импульс (рис.7): |
|
|
|
||||||||||
s(t) = e− |
t2 |
|
|
e− |
ω2a2 |
|
|
|
|
||||
2a2 |
, S(ω) = a |
|
|
|
|
|
|
|
|||||
2π |
|
2 . |
|
|
|
|
|||||||
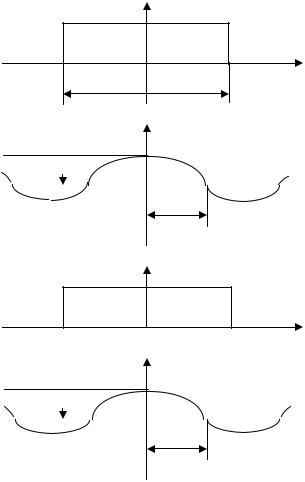
2.4. Спектр дискретизированного сигнала
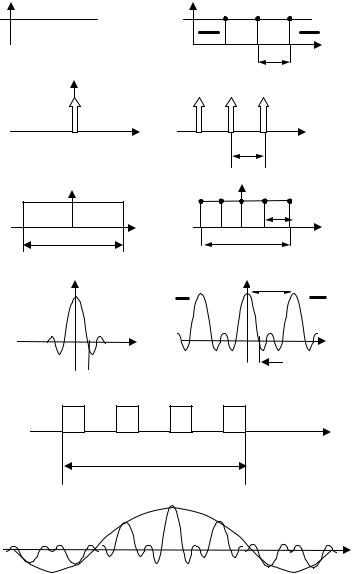
Дискретизация сигнала может привести к его существенному искажению. Как видно из примера, приведенного на рис. 8, сигналы с частотой 4 и 6 Гц, в случае опросов с частотой 5 Гц, воспринимаются как сигнал с частотой 1 Гц. При спектральной функции непрерывного сигнала, показанной на рис. 8 сплошной линией, спектр дискретизированного сигнала содержит бесконечный ряд показанных пунктиром копий спектра исходного сигнала, сдвинутых на nfт , где n - целое число, fт - частота опросов (тактовая). При достаточно высокой частоте дискретизации наложение копий незначительно и исходный сигнал можно восстановить соответствующей фильтрацией. В случае существенного наложения копий спектра восстановление исходного сигнала без искажений невозможно.
6 Гц
4Гц
1 с
S(f)
f, Гц
0 |
fт =5 |
2fт =10 |
Рис.8
Его база fτ = 1/π, если эффективную длительность и ширину спектра определять по уровню e-0,5 ≈ 0,606.
S(t)
 t 0
t 0
S(f)
a)
f
0
S(t)
t
б) τ
S(f)
f
1/τ
 τ
τ 
NT
в)
S(t)
T
S(f)
1/T
T
τ
1/T
0
 1/τ
1/τ
 T
T
Рис.9
t
f
t
f
t
f
На рис. 9 приведены спектры некоторых сигналов. Спектр постоянного сигнала, опрашиваемого с периодом Т - это бесконечный ряд δ - функций - копий спектра постоянного сигнала - рис.9а. Такой же спектр имеет бесконечный ряд δ - импульсов.
Ограниченное число отсчетов можно рассматривать как опросы прямоугольного импульса, соответствующий спектр является повторением копий спектральной функции одиночного импульса - рис.9б. Такой же спектр имеет ограниченная последовательность δ - импульсов.
Ограниченную последовательность прямоугольных импульсов можно считать результатом прохождения пачки δ - импульсов через устройство с прямоугольной импульсной переходной характеристикой. Следовательно, спектр пачки прямоугольных импульсов является произведением спектра пачки δ - импульсов на комплексный коэффициент передачи устройства, равный спектральной функции прямоугольного импульса (рис 9в).
2.5. Характеристики случайных сигналов
Все сигналы, несущие информацию, появляются в приемном устройстве случайным образом: приемник "не знает" заранее, какой символ сообщения был передан. Под влиянием разнообразных случайных факторов принятый сигнал оказывается искаженным, так что один переданный символ может быть принят за другой. Чтобы повысить достоверность передачи информации, необходимо учитывать количественные статистические характеристики сигналов при выборе способов их формирования.
Математическую модель случайного сигнала называют случайной функцией или случайным процессом. В результате опыта случайная функция принимает заранее неизвестный конкретный вид, называемый реализацией случайного процесса, или выборочной функцией. Эта функция не случайная.
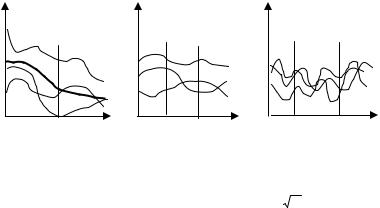
Примеры выборочных функций xi(t) случайной функции X(t) приведены на рис. 10. Множество всех выборочных функций, которое можно представить только мысленно, называется ансамблем. Значения выборочных функций ансамбля, соответствующие конкретному моменту времени t , являются случайной величиной, называемой сечением случайной функции.
Напомним основные, наиболее часто используемые характеристики случайных величин. Функция распределения вероятности дискретной или непрерывной случайной величины F(x) = р(X< x) - это вероятность того, что случайная величина X принимает значение меньше x. Функция плотности распределения вероятности непрерывной случайной величины
р(x) = dF(x)/dx. Величина р(х)dх – это вероятность попадания случайной величины в интервал (х, х+dх). Математическое ожидание (среднее значение) и дисперсия непрерывной случайной величины
|
|
|
∞ |
|
∞ |
2 p(x)dx. |
||
M[X ] = |
x |
= |
∫ xp(x)dx; |
D[X ] = |
∫ (x − |
x |
) |
|
|
|
|
−∞ |
|
−∞ |
|
||
X(t) |
X(t) |
|
|
|
X(t) |
|||
|
|
|
|
|
|
|||
|
X1 |
Х1 |
|
|
|
X2 |
Х2 |
|
|
|
|
|
|
|
|
||
|
|
Х3 |
|
|
|
X3 |
0 |
|
0 |
|
|
0 |
|
|
|
||
t |
t1 |
t2 |
t1 |
t2 |
t |
a) |
б) |
|
|
в) |
|
|
Рис.10 |
|
|
|
|
Среднеквадратичное отклонение (СКО) |
σ = D |
является мерой |
|||
разброса значений случайной величины.
Математическое ожидание и дисперсия случайной функции - это не случайные функции, образованные значениями математического ожидания и дисперсии сечений случайной функции в различные моменты времени. Математическое ожидание случайной функции показано на рис. 10а жирной линией. Разность случайной функции и ее математического ожидания называется центрированной случайной функцией.
Многие практически важные случайные процессы, начиная с некоторого момента времени, могут рассматриваться как установившиеся, стационарные. Математическое ожидание, дисперсия и распределение вероятностей любого сечения стационарной случайной функции не зависят от времени, что значительно упрощает описание процесса. Однако этих характеристик явно недостаточно. На рис. 10 б,в приведены примеры реализации двух случайных процессов с одинаковыми значениями математического ожидания и дисперсии, но разных по характеру. Случайная функция
(б) описывает более низкочастотный процесс, в котором последующие значения сильнее зависят от предыдущих, чем в процессе (в). Степень взаимозависимости значений случайной функции, относящихся к различным моментам времени t1 и t2, описывают корреляционной функцией, которая определяется в общем случае как усредненное произведение центрированных значений случайной функции X(t) в моменты времени t1 и t2 :
M[X (t1)X (t2 )] = R(t1,t2 ). |
(16) |
Функция (16) при не центрированных значениях случайной величины называется ковариационной. Корреляционная функция стационарного случайного процесса зависит только от временного интервала τ = | t2-t1| , а не абсолютного времени:
R(τ ) = M[X (t)X (t +τ )].
В системах связи для описания стационарного случайного процесса, как правило, достаточно среднего значения и корреляционной функции. Процесс называют стационарным в узком (строгом) смысле, если все его статистические характеристики не зависят от начала отсчета времени. Если этим свойством обладают математическое ожидание и корреляционная функция, процесс называют стационарным в широком смысле.
Стационарная функция называется эргодической, если ее характеристики, полученные при исследовании одной реализации на достаточно длительном интервале времени, будут такие же, как при исследовании ансамбля реализаций. Неэргодическим является стационарный процесс, который может происходить в разных модификациях в зависимости от каких-то факторов, не связанных с временем. В частности, процесс рысканья судна на заданном курсе описывается неэргодической случайной функцией. Ее характер зависит от состояния окружающей среды. Об эргодичности процесса обычно судят на основании физических соображений.
Для процесса, эргодического по отношению к среднему значению и корреляционной функции,
M (X ) = lim |
1 |
T ∫/ 2 |
x(t)dt, |
R(τ ) = lim |
1 |
T ∫/ 2x(t)x(t +τ )dt. |
(17) |
|
|
||||||
T →∞ |
T −T / 2 |
|
T →∞ |
T −T / 2 |
|
||
Значение корреляционной функции при τ = 0 равно дисперсии процесса. Нормированная корреляционная функция равна отношению R(τ) к D. Величина
τ k |
= |
1 |
∞∫ |
|
R(τ ) |
|
dτ |
|
|
|
|||||||
|
||||||||
|
|
R(0) 0 |
|
|
|
|
||
называется интервалом корреляции.
На практике интегралы (17) вычисляются как конечные суммы на некотором интервале времени Т. Шаг дискретизации по времени выбирается с учетом характера случайного процесса. Интервал времени Т должен быть достаточно большим для достижения приемлемой точности вычислений.
Спектральный состав случайного сигнала описывается спектральной плотностью мощности. Спектральная плотность мощности случайного сигнала (спектр мощности, энергетический спектр) - это средняя мощность, приходящаяся на полосу в 1 Гц. Понятие спектра мощности можно
ввести следующим образом. Если S(ω) – преобразование Фурье реализации случайного процесса длительности Т, то величина S(ω) 2 имеет физический смысл энергии, а S(ω) 2 /T - средней мощности данной реализации, приходящейся на полосу 1 Гц. Величина lim S(ω) 2 /T (T→∞), усредненная по ансамблю реализаций, будет спектральной плотностью мощности случайного сигнала P(ω). Ее вычисление производится через корреляционную функцию на основании теоремы Винера - Хинчина, согласно которой энергетический спектр и корреляционная функция связаны между собой преобразованием Фурье:
R(τ ) = |
1 |
∞∫ P(ω) cos(ωτ )dω; |
P(ω) = 2∞∫ R(τ ) cos(ωτ )dτ. |
|
|||
|
π 0 |
0 |
|
Использование комплексной формы записи преобразования Фурье в данном случае излишне, т.к. функции R(τ) и P(ω) четные и вещественные. Приведем характеристики некоторых случайных сигналов.
Гауссов процесс. Это стационарная случайная функция, значения которой в любой момент времени характеризуются нормальным (гауссовым) законом распределения вероятности
p(x) = |
|
1 |
|
exp[− |
(x − |
x |
)2 |
], |
|
|
|
|
|
|
|
|
|||
σ |
|
2π |
2σ 2 |
||||||
|
|
|
|
|
|||||
где х - среднее значение, σ2 |
- дисперсия. Гауссов процесс очень часто |
||||||||
используется как модель случайного сигнала. Дело в том, что случайный сигнал обычно зависит от многих случайных взаимно независимых и равнозначных факторов. Согласно центральной предельной теореме распределение вероятностей такого процесса приближается к нормальному. Спектральный состав гауссова процесса может быть любым.
Белый шум. Это стационарный случайный процесс с одинаковой на всех частотах спектральной плотностью мощности N0 (односторонней). Автокорреляционная функция белого шума R(τ) = N0 δ(τ). Такими характеристиками обладает сигнал, составленный из бесконечно малых по длительности импульсов. Во многих случаях можно считать, что в пределах ограниченной полосы пропускания реального устройства спектр помехи равномерен и ее можно принять за белый шум. Белый шум является, в частности, моделью теплового шума, вызванного хаотическим движением электронов в проводниках. Обычно считают, что белый шум является гауссовым процессом.
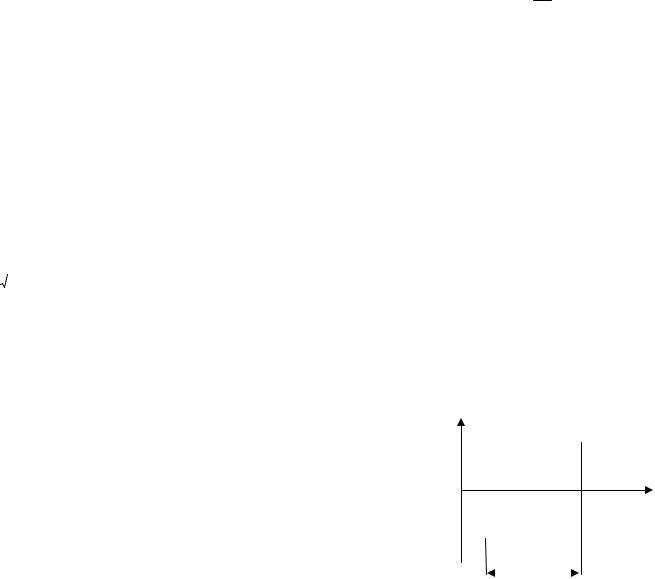
Случайный телеграфный сигнал. Этот сигнал принимает значения +1 и -1 в случайные моменты времени (рис.11). В среднем происходит λ изменений сигнала в единицу времени. Вероятность появления m перепадов сигнала за интервал τ описывается законом Пуассона
P(m,τ ) = am e−a , a = λτ. m!
Вычислим корреляционную функцию этого сигнала. Будем предполагать,
что сигнал опрашивается с шагом |
по времени, |
i - номер опроса, N - |
|||
количество опросов. Тогда τ = k |
|
и |
|
||
|
1 |
|
N |
|
|
R(τ ) = lim |
|
∑ xi xi+k = +1p+ −1p− , |
|||
|
|
||||
N →∞ |
N i=1 |
|
|
||
где p+ и p- -вероятности того, что произведение |
xi xi+k равно +1 и -1 |
||||
соответственно. Величина xi xi+k |
принимает значения +1 и -1 в зависимо- |
||||
сти от того, четное или нечетное число перепадов сигнала произошло на интервале времени τ. Вероятность любого четного числа (m=2n ) и нечетного числа (m=2n+1) перепадов равна соответственно
p = ∞∑ |
a2n |
|
e−a; |
p = ∞∑ |
a2n+1 |
|
e−a. |
|
|
||||||
+ |
(2n)! |
|
− |
(2n +1)! |
|
||
n=0 |
|
n=0 |
|
||||
Используя разложение в ряд
|
±a |
|
1 |
|
|
2 |
|
1 |
|
3 |
|
|
a |
|
−a |
∞ |
a2n |
|
a |
|
−a |
∞ |
a |
2n+1 |
||
e |
|
= 1± a + |
|
|
a |
|
± |
|
a |
|
+..., |
e |
|
+ e |
|
= 2 ∑ |
|
|
; e |
|
− e |
|
= 2 ∑ |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2! |
|
|
|
3! |
|
|
|
|
|
|
n=0 (2n)! |
|
|
|
|
n=0 (2n +1)! |
|||||||
получим
p+ = |
ea + e−a |
|
−a |
= |
1+ e−2a |
, p− = |
1− e |
−2a |
R(τ ) = e |
−2a |
|
||||||||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
. |
|||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Спектральная плотность мощности |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
∞ |
|
−2λ |
|
τ |
|
|
|
|
|
|
|
|
|
4λ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
P(ω) = 2 ∫ |
e |
|
|
|
|
|
cos(ωτ )dτ = |
|
|
|
. |
|
|
|||||||||||
|
|
|
|
|
|
4λ2 + ω2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t-τ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
τ
Рис.11
