
рк+
.pdf
Случайное событие.
Событиями мы будем называть подмножества множества 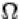 . Говорят, что в результате эксперимента произошло событие
. Говорят, что в результате эксперимента произошло событие 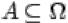 , если в эксперименте произошел один из элементарных исходов, входящих в множество
, если в эксперименте произошел один из элементарных исходов, входящих в множество 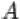 .
.
Операции над событиями (алгебра событий).
1.Объединением 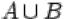 событий
событий 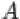 и
и 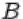 называется событие, состоящее в том, что произошло либо
называется событие, состоящее в том, что произошло либо 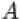 , либо
, либо 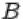 , либо оба события одновременно. На языке теории множеств
, либо оба события одновременно. На языке теории множеств 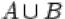 есть множество, содержащее как элементарные исходы из множества
есть множество, содержащее как элементарные исходы из множества 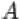 , так и элементарные исходы из множества
, так и элементарные исходы из множества 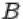 .
.
2.Пересечением 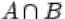 событий
событий 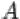 и
и 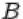 называется событие, состоящее в том, что произошли оба события
называется событие, состоящее в том, что произошли оба события  и
и 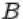 одновременно. На языке теории множеств
одновременно. На языке теории множеств 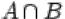 есть множество, содержащее элементарные исходы, входящие в пересечение множеств
есть множество, содержащее элементарные исходы, входящие в пересечение множеств 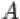 и
и 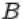 .
.
3.Противоположным (или дополнительным) к событию 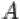 называется событие
называется событие
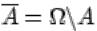 , состоящее в том, что событие
, состоящее в том, что событие 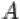 в результате эксперимента не произошло. Т.е. множество
в результате эксперимента не произошло. Т.е. множество 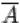 состоит из элементарных исходов, не входящих в
состоит из элементарных исходов, не входящих в 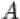 .
.
4. Дополнением 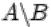 события
события 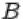 до
до  называется событие, состоящее в том,
называется событие, состоящее в том,
что произошло событие 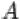 , но не произошло
, но не произошло  . Т.е. множество
. Т.е. множество 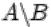 содержит элементарные исходы, входящие в множество
содержит элементарные исходы, входящие в множество 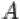 , но не входящие в
, но не входящие в 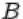
.
Вероятность элементарного события.
Определение 1. Пусть конечное множество Ω = {ω} является пространством элементарных событий, соответствующим некоторому опыту. Пусть каждому ω Ω поставлено в соответствие неотрицательное число P(ω ) , называемое вероятностью элементарного события ω , причем сумма вероятностей всех элементарных событий равна 1, т.е. Σ P (ω ) =1.
ω Ω
Вероятность события.
Вероятность события А равна сумме вероятностей элементарных событий,
входящих в А, т.е. определяется равенством 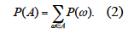
Независимость событий.
События А и В называются независимыми, если Р(АВ) = Р(А) Р(В). Несколько событий А, В, С,… называются независимыми, если вероятность их совместного осуществления равна произведению вероятностей осуществления каждого из них в отдельности: Р(АВС…) = Р(А)Р(В)Р(С)…
Случайная величина.
Случайная величина – это величина, значение которой зависит от случая, т.е. от элементарного события . Таким образом, случайная величина – это функция, определенная на пространстве элементарных событий .
Характеристики случайных величин.
Математическим ожиданием случайной величины Х называется число
M ( X ) X ( )P( ), (4)
т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий.
Пусть Х – случайная величина, М(Х) – ее математическое ожидание, а – некоторое число. Тогда
1) М(а)=а; 2) М(Х-М(Х))=0; 3) М[(X-a)2]=M[(X-M(X))2]+(a-M(X))2.
Дисперсией случайной величины Х называется число 2 D( X ) M [( X M ( X ))2 ].
Пусть Х – случайная величина, а и b – некоторые числа, Y = aX + b. Тогда D(Y) = a2D(X).
Если случайные величины Х и У независимы, то дисперсия их суммы Х+У равна сумме дисперсий: D(X+Y) = D(X) + D(Y).
При описании дифференциации доходов, при нахождении доверительных границ для параметров распределений случайных величин и во многих иных случаях используется такое понятие, как «квантиль порядка р», где 0 < p < 1 (обозначается хр). Квантиль порядка р – значение случайной величины, для которого функция распределения принимает значение р или имеет место «скачок» со значения меньше р до значения больше р (рис.2).
Большое значение в статистике имеет квантиль порядка р = ½. Он называется медианой (случайной величины Х или ее функции распределения F(x)) и обозначается Me(X).
Ясный смысл имеет такая характеристика случайной величины, как мода – значение (или значения) случайной величины, соответствующее локальному максимуму плотности вероятности для непрерывной случайной величины или локальному максимуму вероятности для дискретной случайной величины.
Каждая из трех характеристик – математическое ожидание, медиана, мода – описывает «центр» распределения вероятностей. Понятие «центр» можно определять разными способами – отсюда три разные характеристики.
Функции распределения числовой случайной величины: дискретные, непрерывные, смешанные.
Распределение числовой случайной величины – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Распределение может быть задано с помощью т.н. функции распределения F(x) = P(X<x), определяющей для всех действительных х вероятность того, что случайная величина Х принимает значения, меньшие х.
Дискретные функции распределения соответствуют дискретным случайным величинам, принимающим конечное число значений или же значения из множества, элементы которого можно перенумеровать натуральными числами (такие множества в математике называют счетными).
Непрерывные функции распределения не имеют скачков. Они монотонно возрастают 1 при увеличении аргумента – от 0 при x до 1 при x . Случайные величины, имеющие непрерывные функции распределения, называют непрерывными.
Смешанные функции распределения встречаются, в частности, тогда, когда наблюдения в какой-то момент прекращаются. Например, при анализе статистических данных, полученных при использовании планов испытаний на надежность, предусматривающих прекращение испытаний по истечении некоторого срока. Или при анализе данных о технических изделиях, потребовавших гарантийного ремонта.
Теорема Муавра-Лапласа.
Теорема Муавра-Лапласа. Для любых чисел a и b, a<b, имеем
|
|
|
Y np |
|
|
|
|
|
|
|
|
|
|
||
lim P a |
|
|
|
b |
(b) (a), |
||
|
|
|
|||||
n |
|
np(1 p) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Ф(х) – функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
Центральная предельная теорема (ЦПТ).
Центральная предельная теорема (для одинаково распределенных слагаемых). Пусть X1, X2,…, Xn, …– независимые одинаково распределенные случайные величины с математическими ожиданиями M(Xi) = m и дисперсиями D(Xi) = 2 , i = 1, 2,…, n,… Тогда для любого х существует предел
|
X |
1 X |
2 |
... X n nm |
|
|
|||
lim P |
|
|
|
|
|
|
x |
(x), |
|
|
|
|
|
|
|
||||
|
|
n |
|||||||
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
где Ф(х) – функция стандартного нормального распределения.
ТЕМА2
Необходимость выборочных исследований. Термин "выборочные
исследования" применяют, когда невозможно изучить все единицы представляющей интерес совокупности. Приходится знакомиться с частью совокупности – с выборкой, а затем с помощью статистических методов и моделей переносить выводы с выборки на всю совокупность. Выборочные исследования – способ получения статистических данных и важная часть прикладной статистики. В качестве примера рассмотрим выборочные исследования предпочтений потребителей, которые часто проводят специалисты по маркетингу.
РАЗЛИЧНЫЕ ВИДЫ ФОРМУЛИРОВОК ВОПРОСА,ИХ ДОСТОИНСТВА И НЕДОСТАТКИ.
В маркетинговых и социологических опросах используют тритипа вопросов - закрытые, открытые и полузакрытые, они же полуоткрытые. При ответе на закрытые вопросы респондент может выбирать лишь из сформулированных составителями анкеты вариантов ответа. В качестве ответа на открытые вопросы респондента просят изложить свое мнение в свободной форме. Полузакрытые, они же полуоткрытые вопросы занимают промежуточное положение - кроме перечисленных в анкете вариантов, респондент может
добавить свои соображения.
Преимущество открытых вопросов состоит в том, что респондент может свободно высказать свое мнение так, как сочтет нужным. Их недостаток - в сложности сопоставления мнений различных респондентов. Для такого сопоставления и получения сводных характеристик организаторы опроса вынуждены сами шифровать ответы на открытые вопросы, применяя разработанную ими схему шифровки.
Преимущество закрытых вопросов в том и состоит, что такую шифровку проводит сам респондент. Однако при этом организаторы опроса уподобляются древнегреческому мифическому персонажу Прокрусту. Как известно, Прокруст приглашал путников заночевать у него. Укладывал их на кровать. Если путник был маленького роста, он вытягивал его ноги так, чтобы они доставали до конца кровати. Если же путник оказывался высоким и ноги его торчалион обрубал их так, чтобы достигнуть стандарта: "рост" путника должен равняться длине кровати. Так и организаторы опроса, применяя закрытые вопросы, заставляют респондента "вытягивать" или "обрубать" свое мнение, чтобы выразить его с помощью приведенных в формулировке вопроса возможных ответов.
ГИПЕРГЕОМЕТРИЧЕСКАЯ МОДЕЛЬ ВЫБОРКИ.
Гипергеометрическое распределение имеет место при выборочном контроле конечной совокупности объектов объема N по альтернативному признаку. Каждый контролируемый объект классифицируется либо как обладающий признаком А, либо как не обладающий этим признаком. Гипергеометрическое распределение имеет случайная величина Y, равная числу объектов, обладающих признаком А в случайной выборке объема n, где n<N. Например, число Y дефектных единиц продукции в случайной выборке объема n из партии объема Nимеет гипергеометрическое распределение, если n<N. Другой пример – лотерея. Пусть признак А билета – это признак «быть выигрышным». Пусть всего билетов N, а некоторое лицо приобрело n из них. Тогда число выигрышных билетов у этого лица имеет гипергеометрическое распределение.
Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид

(20)
где D – число объектов, обладающих признаком А, в рассматриваемой совокупности объема N. При этом yпринимает значения от max{0, n - (N - D)} до min{n, D}, при прочих y вероятность в формуле (20) равна 0. Таким образом, гипергеометрическое распределение определяется тремя параметрами – объемом генеральной совокупности N, числом объектов D в ней, обладающих рассматриваемым признаком А, и объемом выборки n.
Простой случайной выборкой объема n из совокупности объема N называется
выборка, полученная в результате случайного отбора, при котором любой из 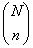 наборов из n объектов имеет одну и ту же вероятность быть отобранным.
наборов из n объектов имеет одну и ту же вероятность быть отобранным.
Методы случайного отбора выборок респондентов (опрашиваемых) или единиц штучной продукции рассматриваются в инструктивно-методических и нормативнотехнических документах. Один из методов отбора таков: объекты отбирают один из другим, причем на каждом шаге каждый из оставшихся в совокупности объектов имеет одинаковые шансы быть отобранным. В литературе для рассматриваемого типа выборок используются также термины «случайная выборка», «случайная выборка без возвращения».
Поскольку объемы генеральной совокупности (партии) N и выборки n обычно известны, то подлежащим оцениванию параметром гипергеометрического распределения является D. В статистических методах управления качеством продукции D – обычно число дефектных единиц продукции в партии. Представляет интерес также характеристика распределения D/N – уровень дефектности.
Для гипергеометрического распределения
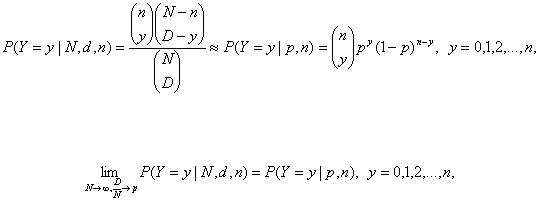
Последний множитель в выражении для дисперсии близок к 1, если N>10nЕсли при этом сделать замену p =D/N, то выражения для математического ожидания и дисперсии гипергеометрического распределения перейдут в выражения для математического ожидания и дисперсии биномиального распределения. Это не случайно. Можно показать, что
при N>10n, где p = D/N. Справедливо предельное соотношение
и этим предельным соотношением можно пользоваться при N>10n.
Поскольку гипергеометрическое распределение хорошо приближается биномиальным, если объем выборки по крайней мере в 10 раз меньше объема всей совокупности (в рассматриваемом случае это так), то правомерно использование
биномиальной модели, согласно которой мнение респондента (ответы на вопросы анкеты) рассматривается как случайный вектор, а все такие вектора независимы между собой. Другими словами, можноиспользовать модель простой случайной выборки.
Асимптотическое распределение выборочной доли Интервальное оценивание доли метод проверки гипотезы о равенстве долей(пирсон).
Зададимся некоторой вероятностью (обычно = 0,05; подробнее об этой величине будет сказано ниже). Можно утверждать, что существует такое , для которого имеет место соотношение:
|
|
|
|
|
|
|
|
Р ( X - х |
X + ) |
= 1 - , |
(6.1) |
||||

Интервал вида (1) называется доверительным.
Чтобы понять, как находится , напомним, что среднее арифметическое X для гипотетического бесконечного количества выборок имеет распределение N (
х, x ).
 n
n
Доверительный интервал для доли
Доверительные интервалы могут быть построены отнюдь не только для генеральной средней и медианы, но и для многих других параметров распределений: дисперсии, коэффициента корреляции и т.д. Мы рассмотрим с соответствующей точки зрения ешё только одну статистику: долю встречаемости какого-либо значения одного из рассматриваемых признаков. Смысл соответствующей содержательной задачи представляется ясным. Представим, скажем, что доля мужчин в выборке оказалась равной 54%. Встает вопрос о какой-то оценке этой доля в генеральной совокупности. Как и выше, ответ на этот вопрос будет дан с помощью построения доверительного интервала для генеральной доли (т.е. – вероятности встречаемости свойства «быть мужчиной» среди объектов изучаемой генеральной совокупности).
Обозначения: p - упомянутая доля для выборки, - для генеральной совокупности, q = 1-p, sр - средняя ошибка выборки для доли p. Для любого уровня значимости можно найти такое z, что будет справедливым соотношение:
Р (р - р + ) = 1 - , где
= z |
pq |
, т.е. |
|
n |
|||
|
|

Р (р - z |
pq |
р + z |
pq |
) = 1 - |
(6) |
|||||
|
|
|
||||||||
n |
n |
|||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
Заметим, что величина Sр = |
|
pq |
|
- это средняя ошибка выборки для доли |
||||||
|
n |
|||||||||
|
|
|
|
|
|
|
|
|
||
p (т.е. средний разброс таких долей, вычисленных для всех мыслимых выборок). Если как-то удастся определить максимально возможную величину , то, по аналогии с соответствующими рассмотрениями выше, эта величина будет называться предельной ошибкой выборки для доли.
Подчеркнем, что значения p и q обычно рассчитываются для выборки, хотя в идеале здесь тоже (как и в случае расчета доверительного интервала для математического ожидания) должны быть генеральные показатели.
Формула для вычисления Sр фактически совпадает с формулой для вычисления Sх при определенном взгляде на принятое во внимание значение рассматриваемого признака. Рассмотрим этот аспект более подробно, поскольку этот факт имеет довольно принципиальное значение для выработки подходов к анализу социологических данных..
