(Программа 50-МКЭ-1-балка.mcd)

Расчет балки примитивно прост, если надо определить лишь одну первую собственную частоту. Для определения спектра собственных частот и получения формы колебаний необходимо использовать метод конечных элементов. Простейшим вариантом этого метода и является матричный метод перемещений.

Целью расчета является определение вектора собственных частот балки. В примере 36 балка рассматривалась, как система с одной степенью свободы, и соответственно определена была только одна собственная частота (первая).

Для определения вектора собственных частот надо рассмотреть балку, как систему с несколькими степенями свободы.

Статический расчет балки

Поясним суть матричного метода.

1.Заданная стержневая система (в нашем случае балка) разбивается на элементы — стержни.

2.Для каждого элемента составляется основное уравнение матричного метода,

представляющее собой закон Гука в обобщенном виде F = K , где F — вектор сил, — вектор перемещений, K — матрица жесткости.

3.Уравнения для отдельных элементов объединяются в единую систему уравнений, решение которой дает вектор узловых перемещений стержневой системы.

4.Зная узловые перемещения системы, можно определить внутренние усилия в стержнях, напряжения, собственные частоты и т. д.

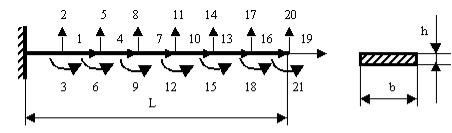
На рисунке 50П.1 показано разбиение заданной балки на элементы — стержни. На рис. 50П.2 — исходные данные к расчету.

Рис. 50П.1. Расчетная схема балки

В примерах 50, 51, 52 расчет ведется без учета размерностей, так как элементы матриц в этих примерах имеют разные размерности. Mathcad считает это недопустимым.

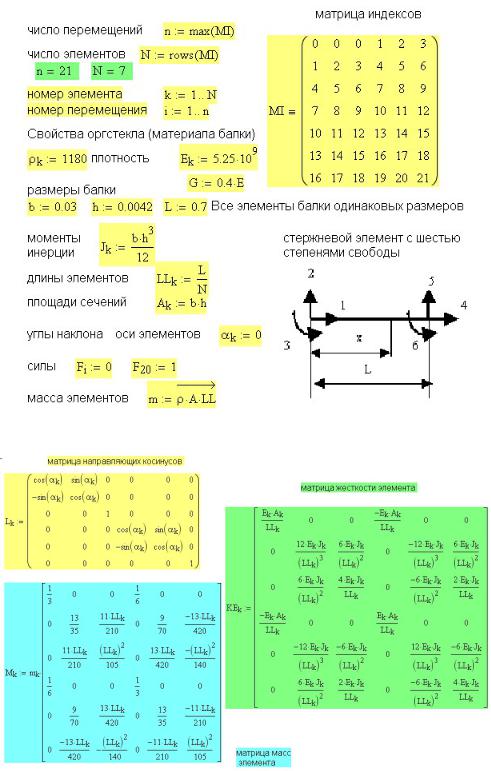
Плоский стержневой элемент, показанный на рис. 50П.2, имеет 6 степеней свободы (узловых перемещений). Соответственно в уравнении F = K векторы сил F и перемещений содержат по 6 элементов. Матрица жесткости К — стандартная размерностью 6×6 — приведена на рис. 50П.3.

173

Рис. 50П.2 Исходные данные к расчету

Рис. 50П.3. Стандартные матрицы для плоского стержневого элемента

В матричном методе используются 2 системы координат: локальная и глобальная. Локальная система — своя для каждого элемента. Ось х направлена вдоль оси стержня. Начало локальной нумерации в начале координат. Глобальная система — единая для всей стержневой системы. Выбор начала глобальных координат и направление осей произвольные. Связь между этими системами координат описывается матрицей направляющих косинусов.

Положение плоского стержневого элемента характеризуется 6-ю независимыми узловыми перемещениями (6-ю степенями свободы — по 3 в каждом узле). Связь между узловыми перемещениями элемента в локальной и глобальной системах

направляющих косинусов.

Поскольку каждому узловому перемещению соответствует своя узловая сила, то

Связь между матрицами жесткости: K в локальной и K в глобальной системах координат K = LT K L .

В плоской задаче для задания матрицы направляющих косинусов, приведенной на

174рис. 50П.3, достаточно для каждого элемента задать угол α между осями х (локальной и глобальной).

В нашем примере консольная балка разбита на 7 элементов. У каждого элемента по 6

узловых перемещений. Значит, в 7 матричных уравнениях содержится 7×6=42 перемещения. Как показано на рис. 50П.1, рассматриваемая балка имеет 21 узловое перемещение (по 3 в каждом узле и в заделке нет перемещений). Чтобы их найти, надо систему из 42 уравнений с 42 неизвестными превратить в систему из 21 уравнения с 21 перемещением. Эта задача выполняется с помощью матрицы соответствия индексов (рис. 50П.2).

Матрица индексов показывает, какому номеру перемещения всей стержневой системы соответствует локальный номер перемещения каждого элемента в глобальной системе координат.

С помощью матрицы индексов формируется матрица жесткости системы путем суммирования соответствующих коэффициентов жесткости.

Коэффициент жесткости системы Ki, j равен сумме коэффициентов жесткости элементов, которым в матрице индексов одновременно принадлежат индексы i и j .

Выражение для суммирования коэффициентов жесткости приведено на рис. 50П.4, внизу.

Рис. 50П.4. Формирование матрицы жесткости системы

При расчете в Mathcad возникает неожиданная трудность. Для удобства работы с матрицами введено ORIGIN=1, но в таком случае в матрицах не может быть элементов с номером 0. Чтобы выйти из этого тупика, в матрице индексов 0 заменен на n+1, где n — максимальный номер перемещения системы. При этом вместо матрицы размерностью n×n получается матрица размерностью (n+1)×(n+1). После формирования матрицы жесткости лишние строку и столбец удаляем с помощью функции submatrix.

ПРИМЕЧАНИЕ

Нуль в матрице индексов означает отсутствие перемещения системы по данному направлению.

После формирования матрицы жесткости системы выполняется решение системы линейных алгебраических уравнений путем обращения матрицы жесткости системы (рис. 50П.5). В результате решения получается вектор узловых перемещений системы в глобальных осях координат.

Перемещения элементов в глобальных осях определяются с помощью матрицы индексов путем присвоения перемещениям элементов соответствующих перемещений системы.

Далее определяются перемещения элементов в локальных осях координат с помощью матрицы направляющих косинусов, затем узловые силы, действующие на элементы, в локальных осях координат из основного уравнения матричного метода,

записанного для элемента в локальных осях координат F e = Ke e . Результаты статического расчета перемещений и усилий, действующих на балку, приведены на рис. 50П.5.