Пример 32. Расчет многопролетной балки |
||
118 |
|
на изгиб. |
|
(Программа 32-n-opor2.mcd) |
|
Если у многопролетной балки нет заделки на одном из ее концов, а есть только |
||
шарнирные опоры, то при работе в Mathcad расчет становится немного сложнее. Для |
||
грузовой и всех единичных систем потребуется определять опорные реакции. |
||
Условная схема расчета такой балки показана на рис. 32П.1. В качестве основной |
||
статически определимой системы возьмем балку на двух опорах. Оставляем крайние |
||
левую и правую опоры. Остальные отбрасываем и заменяем неизвестными |
||
реакциями |
Xi . Грузовая и одна из единичных систем показаны на рис. 32П.2. |
|
Исходные данные к расчету приведены на рис. 32П.3. |
||
y |
M0 |
q |
|
|
F |
|
|
x |
|
|
q |
|
aM |
|
|
LRi |
|
|
aF |
|
|
aq |
|
|
|
bq |
|
|
x |
|
|
L |
|
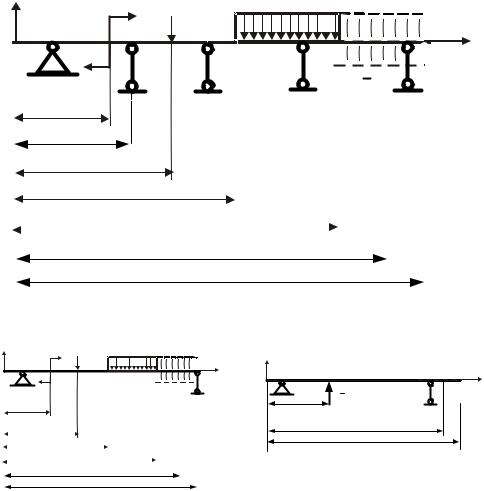
Рис. 32П.1. Условная схема нагружения многопролетной балки |
|
|
Грузоваясистема |
y |
q |
M 0 |
|
|
F |
|
x |
|
-q |
|
aM |
|
aF |
|
aq |
|
bq |
|
x |
|
L |
|
i - яѝединичнаяѝсистема |
y |
|
|
x |
LL |
F = 1 |
|
x |
|
L |
Рис. 32П.2. Расчетные схемы для многопролетной балки
119
Рис. 32П.3. Исходные данные к расчету многопролетной балки
В примере12 (Определение внутренних усилий в балке на двух опорах)
опорные реакции определялись с помощью вычислительного блока Given-Find. При решении данной задачи этот блок вызывается тысячи раз и вычисление продолжается очень долго (больще 5 минут). Для ускорения процесса я решил вместо блока GivenFind вставить в программу формулы для определения реакций (рис. 32П.4). Реакции для грузовой системы вычисляются только один раз,. Там же на рис. 32П.4 показана эпюра изгибающих моментов для грузовой системы. а реакции единичной системы многократно, поэтому их определение оформлено в виде подпрограммы (рис. 32П.5), в которую вставлены конкретные формулы, полученные при преобразовании уравнений равновесия балки Замена вычислительного блока Given-Find на приведенную подпрограмму привело к уменьшению времени расчета примерно в сто раз.
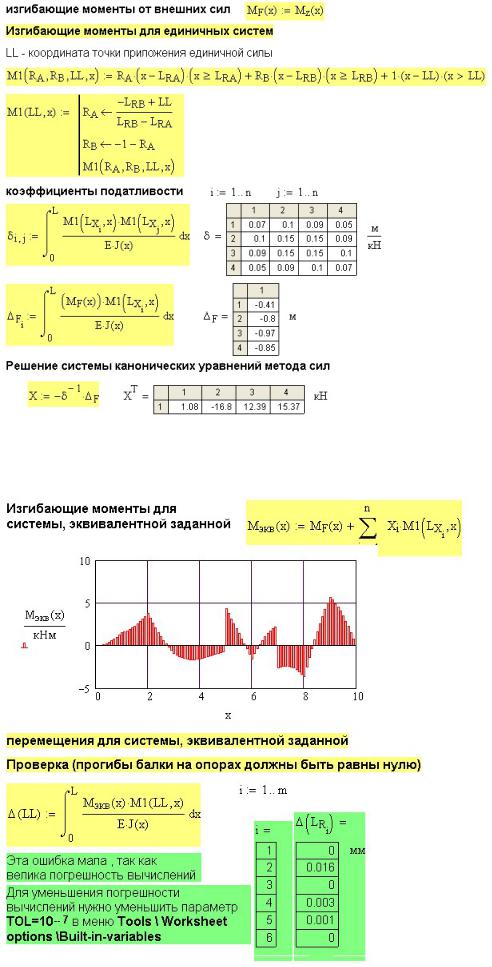
Рис. 32П.4. Внутренние усилия в грузовой системе
120
Рис. 32П.5. Расчет многопролетной балки методом сил
После определения внутренних усилий с учетом реакций последующие вычисления проводятся также как в примере 31 и приведены на рис. 32П.5 – 32П.7.
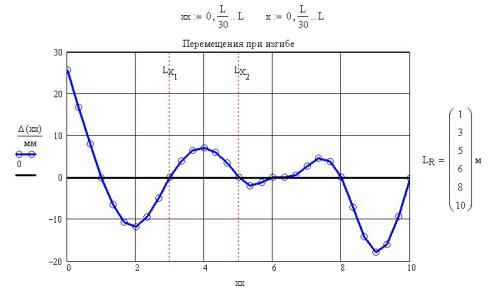
Рис. 32П.6. Результаты расчета многопролетной балки
121
Рис. 32П.7. Проверка правильности расчета многопролетной балки
|
Пример 33. Подбор размеров сечения |
122 |
сжатого стержня. |
(Программа 33-ustoi1.mcd)
Для стержня круглого поперечного сечения длиной L = 2 м, нагруженного силой F = 80 кН (рис. 33П.1), требуется определить диаметр стержня.
Рис. 33П.1. Схема нагружения стержня
Поскольку размеры сечения стержня неизвестны, а значит и гибкость стержня λ неизвестна, то расчет ведется итерационным методом.
Исходные данные для расчета стержня приведены на рис. 33П.1. На рис. 33П. 2 приведены справочные данные: зависимость коэффициента снижения допускаемого
напряжения ϕ от гибкости стержня λ . Для автоматизации расчета введена функция интерполяции и построен график зависимости ϕ от λ (рис. 33П.2).
Рис. 33П.2. Зависимость коэффициента снижения допускаемого напряжения ϕ от гибкости стержня λ .
В справочниках приводятся значения коэффициента ϕ для λ ≤ 200. На всякий случай, в массивы данных введено ϕ = 0, 01 для λ =1000 ,так как в ходе
итерационного процесса могут появляться значения λ > 200. На графике это значение не показано.
Поскольку расчет выполняется многократно, он оформлен в виде программы (рис. 33П.3), состоящей из головной программы D , внутри которой многократно вызывается подпрограмма dλ определения диаметра и гибкости стержня.
123
Рис. 33П.3. Программа расчета диаметра сжатого стержня
В начале головной программы введены значения коэффициента ϕ : в начале ϕ1, в
конце итерации |
ϕ2 и счетчик числа итераций |
j . В нашем расчете для первой |
итерации взят |
совершенно неправдоподобный |
коэффициент ϕ1 = 0,9 , чтобы |
показать, что и в этом случае расчет сходится довольно быстро.
Затем следует итерационный цикл, начинающийся оператором while — повторять цикл до выполнения заданного критерия (пока расхождение между ϕ1 и ϕ2 не
станет меньше 0,1%).
Вся программа выделена длинной вертикальной чертой слева, итерационный цикл выделен второй вертикальной чертой.
В подпрограмме dλ последовательно вычисляются допускаемые напряжения на устойчивость σу , площадь сечения A , диаметр стержня d , момент инерции J ,
радиус инерции i и гибкость стержня λ .
В конце итерации определяется новое значение коэффициента ϕ с помощью функции интерполяции ϕ(λ), показанной на рис. 33П.2.
Для начала следующей итерации вычисляется усредненное новое значение ϕ1.
Далее следует возврат к началу цикла итерации, но перед этим организуется вывод результатов расчета каждой итерации.
Значения ϕ, λ, d на каждой итерации записываются в массивы ϕϕ, λλ,dd .
Поскольку программа выводит численные значения последнего оператора, то в качестве последнего оператора поставлен составной массив: вектор, содержащий три вложенных массива и записанный в виде строки для экономии места в программе.
При отладке программ в составной массив можно включать результаты любых внутренних операторов программы.
Рис. 33П.4. Результаты расчета на каждой итерации
Результаты расчета показаны на рис.33П.4. Несмотря на высокую точность расчета (0,1%) четырех итераций оказалось достаточно для достижения указанной точности.
|
Пример 34. Определение критических |
124 |
нагрузок энергетическим методом. |
(Программа 34-ustoi2.mcd)
Пример 1
Для схемы Эйлера (рис. 34П.1) определим критическую силу энергетическим методом.
Рис. 34П.1. Результаты расчета на каждой итерации
В общем случае изогнутую ось стержня будем аппроксимировать полиномом степени m
m
u(x) = C0 +C1x + C2 x2 + C3 x3 +... = ∑Ci xi .
i=0
Значения коэффициентов Ci определяем из граничных условий (условий
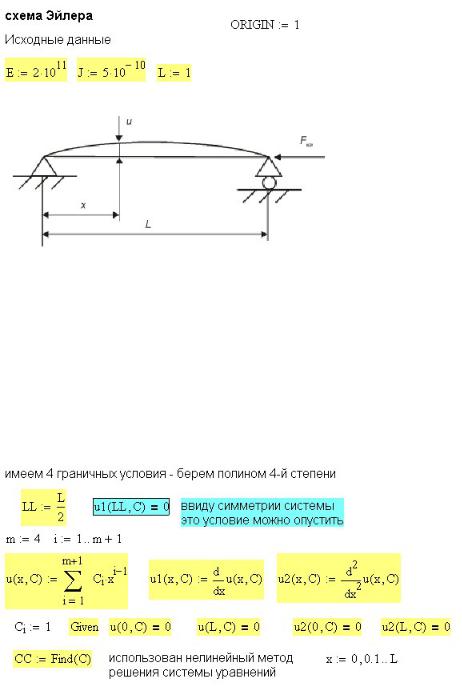
закрепления стержня), решая систему уравнений с помощью вычислительного блока given – find (рис. 34П.2). Поскольку в программе нумерация коэффициентов начинается с 1 (ORIGIN=1), вид выражения полинома отличается от написанного выше.
Рис. 34П.2. Определение коэффициентов аппроксимирующего полинома
Для стержня шарнирно закрепленного с двух концов граничными условиями
являются равенство нулю |
прогиба на опорах u(0) = 0 |
и u(L) = 0 , |
а также |
|||
равенство нулю изгибающих моментов на концах стержня M (0) = 0 и M (L) = 0 . |
||||||
Но изгибающий момент |
пропорционален второй |
производной от |
прогиба |
|||
′′ |
|
′′ |
= 0 |
и u |
′′ |
|
M = EJu (x) , следовательно, на концах стержня u |
(0) |
(L) = 0 . |
|
|||
ПРИМЕЧАНИЕ
Внутри блока given – find нельзя использовать в качестве условий производные. Граничные условия не могут вычисляться внутри блока given – find, поэтому каждой производной в программе присваивается имя функции, а в вычислительный блок записывается значение функции от заданного аргумента, например, для
второй производной u2(0, C) = 0 .
В рассмотренном примере используется полином четвертой степени, имеющий 5 неизвестных коэффициентов, следовательно, в вычислительный блок надо подставить 5 граничных условий. Однако в виду симметрии системы пятое условие
125(равенство нулю угла поворота сечения посередине балки) выполняется автоматически.
Кроме того, в формулу Рэлея входят лишь первая и вторая производные от прогиба, поэтому в расчете используются не 5, а 4 коэффициента. Кроме того, два коэффициента оказались равны нулю.
В общем, подбирая степень полинома, смотрите на его график. Главное, чтобы выполнялись граничные условия. Помните, что решение мы ищем приближенное, что подбираемый "на глазок" полином никак не учитывает различие в форме и размерах сечений по длине стержня.
Решение системы нелинейных алгебраических уравнений требует использования нелинейных методов решения. Щелкните правой кнопкой мыши на имени функции find и в открывшемся контекстном меню выберите метод решения Nonlinear.
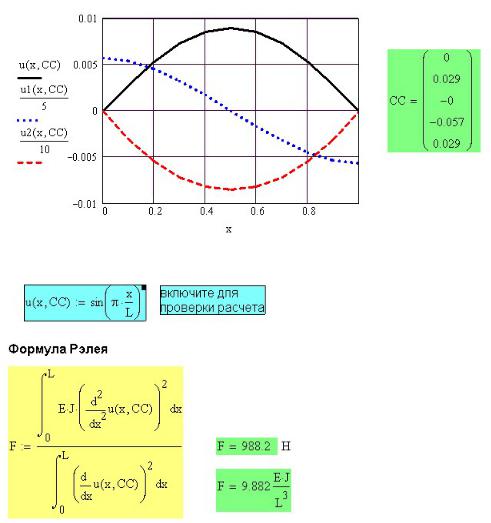
На рис. 34П.3 приведен вектор коэффициентов полинома и графики прогиба стержня и его первой и второй производных.
Рис. 34П.3. Графики аппроксимирующего полинома и его первой и второй производных
Рис. 34П.4. Формула Рэлея определения критической силы
На рис. 34П.4 записана формула Рэлея и приведено расчетное значение Pкр .
Выведено численное значение критической силы для заданного стержня и числовой коэффициент при буквенном выражении.
На том же рисунке предлагается проверить другой вид аппроксимации уравнения изогнутой оси стержня. При выводе формулы Эйлера использовалась синусоида для описания изогнутой оси. Включите выражение синусоиды и убедитесь, что результаты расчета совпадают для обоих видов аппроксимации изогнутой оси стержня.
Пример 2
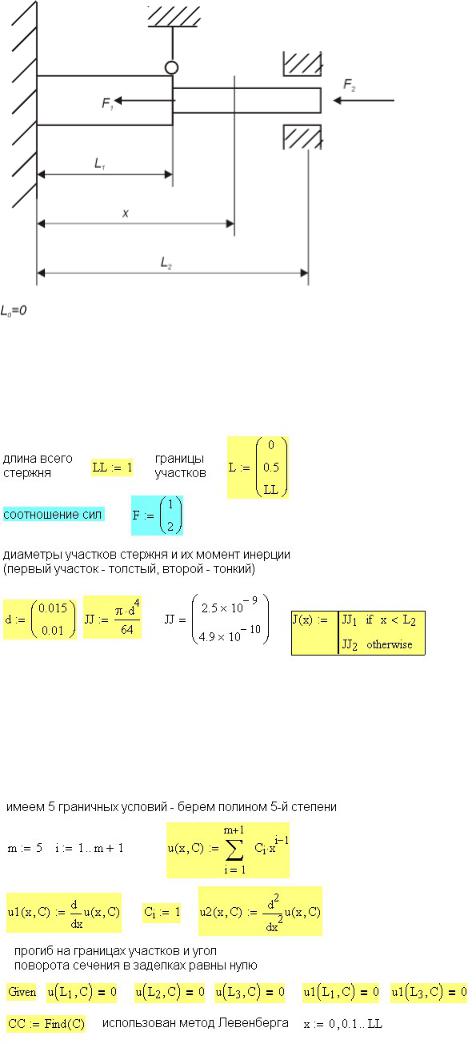
Определить нагрузку, соответствующую потере устойчивости для ступенчатого стального стержня с двумя заделками и промежуточной шарнирной опорой, нагруженного двумя силами (рис. 34П.5).
126
Рис. 34П.5. Схема нагружения ступенчатого стального стержня
Нижняя заделка неподвижная, верхняя подвижная. Промежуточная шарнирная опора установлена на границе нижней (толстой) части стержня и верхней (тонкой). Поскольку ищем нагрузку, то задано лишь соотношение сил на свободном конце и на
границе участков F1 = 2F2 . Исходные данные для расчета приведены на рис. 34П.6.
Рис. 34П.6. Исходные данные для расчета на устойчивость ступенчатого стержня
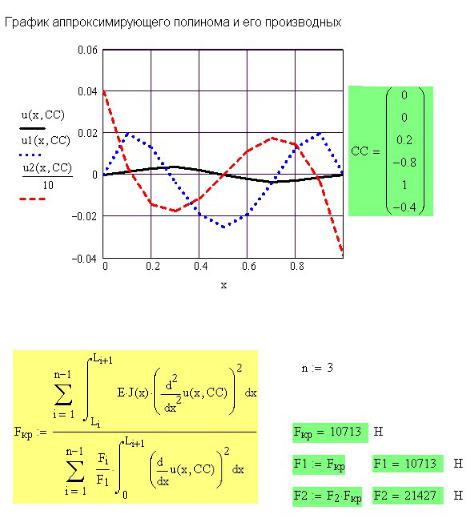
Граничными условиями для изогнутой оси стержня являются равенство нулю прогибов в заделках и шарнирной опоре и равенство нулю углов поворота в заделках. Имеем 5 граничных условий. Ищем полином 5-й степени (рис.34П.7). Графики полинома и его первой и второй производных показаны на рис. 34П.8. Критические
значения сил F1 и F2 приведены на рис. 34П.9.
Рис. 34П.7. Подбор коэффициентов аппроксимирующего полинома
127
Рис. 34П.8. Графики аппроксимирующего полинома и его производных
Рис. 34П.9. Определение критических нагрузок на ступенчатый стержень
Приведенная программа позволяет приближенно определять критическую нагрузку при действии нескольких сил и нескольких участках различной формы сечения. Степень полинома определяем, исходя из числа граничных условий и "на глазок" по виду графика полинома и его производных.