
3_bilet_diff
.docx№3. Однородные уравнения. Линейные уравнения первого порядка. Уравнения Бернулли и Риккати.
Однородные уравнения
Функция
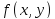 называется однородной
функцией своих аргументов
степени
называется однородной
функцией своих аргументов
степени
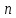 ,
если справедливо тождество
,
если справедливо тождество
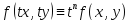 .
.
Например,
функция
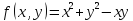 есть однородная функция второй степени,
т.к.
есть однородная функция второй степени,
т.к.
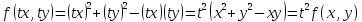 .
.
При
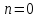 имеем функцию нулевой степени. Например,
имеем функцию нулевой степени. Например,
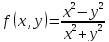 есть
однородная функция нулевой степени,
так как
есть
однородная функция нулевой степени,
так как

Дифференциальное
уравнение вида
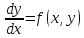 называется однородным
относительно x и y,
если
называется однородным
относительно x и y,
если
 есть однородная функция своих аргументов
нулевой степени. Однородное уравнение
всегда можно представить в виде
есть однородная функция своих аргументов
нулевой степени. Однородное уравнение
всегда можно представить в виде
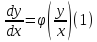
Вводя
новую искомую функцию
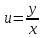 , уравнение (1) можно привести к уравнению
с разделяющими переменными:
, уравнение (1) можно привести к уравнению
с разделяющими переменными:
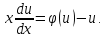
Если
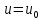 есть корень уравнения
есть корень уравнения
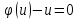 ,
то решение однородного уравнения будет
,
то решение однородного уравнения будет
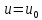 или
или
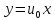 (прямая, проходящая через начало
координат).
(прямая, проходящая через начало
координат).
Замечание:
при решении однородных уравнений
необязательно приводить их к виду (1).
Можно сразу сделать подстановку
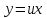 .
.
Уравнения, приводящиеся к однородным
А. Рассмотрим дифф. ур-е вида
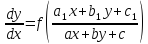
Оно
приводится к однородному с помощью
переноса начала координат в точку
пересечения прямых
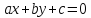 и
и
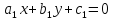 .
Если эти прямые не пересекаются, то
.
Если эти прямые не пересекаются, то
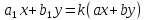 ;
след-но, ур-е имеет вид
;
след-но, ур-е имеет вид
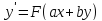 и приводится к ур-ю с разделяющимися
переменными заменой
и приводится к ур-ю с разделяющимися
переменными заменой
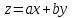 (или
(или
 .
.
Б.
Некоторые ур-я можно привести к однородным
заменой
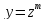 .
Число
.
Число
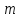 обычно заранее не известно. Чтобы его
найти, надо в уравнении сделать замену
обычно заранее не известно. Чтобы его
найти, надо в уравнении сделать замену
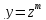 .
Требуя, чтобы ур-е было однородным,
найдём число
.
Требуя, чтобы ур-е было однородным,
найдём число
 ,
если это возможно. Если же этого сделать
нельзя, то ур-е не приводится к однородному
этим способом.
,
если это возможно. Если же этого сделать
нельзя, то ур-е не приводится к однородному
этим способом.
Линейные уравнения первого порядка
Так называется ур-е, линейное относительно неизвестной функции и её производной. Оно имеет вид
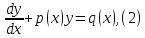
где
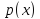 и
и
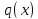 –
заданные функции от
–
заданные функции от
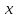 ,
непрерывные в той области, в которой
требуется проинтегрировать уравнение
(2).
,
непрерывные в той области, в которой
требуется проинтегрировать уравнение
(2).
Если
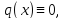 то уравнение (2) называется линейным
однородным. Оно является
уравнением с разделяющимися переменными
и имеет общее решение
то уравнение (2) называется линейным
однородным. Оно является
уравнением с разделяющимися переменными
и имеет общее решение
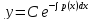
Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной, который состоит в том, что решение уравнения (2) ищется в виде
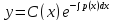
Где
 – новая неизвестная функция от
– новая неизвестная функция от
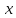 .
.
Уравнение Бернулли
Имеет
вид
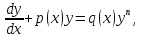
где
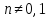 (при
(при
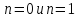 это уравнение является линейным).
это уравнение является линейным).
С
помощью замены переменной
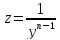 уравнение Бернулли приводится к линейному
уравнению и интегрируется как линейное.
уравнение Бернулли приводится к линейному
уравнению и интегрируется как линейное.
Уравнение Риккати
Дифференциальное уравнение первого порядка вида
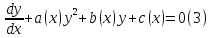
где
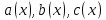 – известные функции, называется
уравнением Риккати. Если коэффициенты
– известные функции, называется
уравнением Риккати. Если коэффициенты
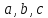 в уравнении Риккати постоянны, то
уравнение допускает разделение
переменных, и мы сразу получаем общий
интеграл
в уравнении Риккати постоянны, то
уравнение допускает разделение
переменных, и мы сразу получаем общий
интеграл
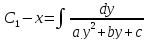
Уравнение Риккати в общем случае не интегрируется в квадратурах.
Свойства уравнения Риккати:
-
Если известно какое-нибудь частное решение
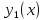 уравнения Риккати то его общее решение
может быть получено при помощи квадратур.
Для этого нужно сделать замену
уравнения Риккати то его общее решение
может быть получено при помощи квадратур.
Для этого нужно сделать замену
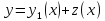 ,
подставить в ур-е (3) и всё сведётся к
частному случаю ур-я Бернулли.
,
подставить в ур-е (3) и всё сведётся к
частному случаю ур-я Бернулли. -
Если известны два частных решения уравнения (3), то его общий интеграл находится одной квадратурой (например, для ур-я
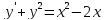 в левой части будут члены, подобные
членам правой части, если взять
в левой части будут члены, подобные
членам правой части, если взять
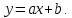 Подставим
и найдём
Подставим
и найдём
 ).
).
Ссылки
Однородные ур-я и приводящиеся к однородным
Краснов/Киселев – стр. 26 Филиппов – стр. 17
Линейные ур-я первого порядка
Краснов/Киселев – стр. 32 Филиппов – стр. 20
Ур-е Бернулли
Краснов/Киселев – стр. 37
Филиппов – стр. 21
Ур-е Риккати
Краснов/Киселев – стр. 51
Филиппов – стр.22
