
Математическое моделирование в естественных науках
..pdfрасположению крана подачи тетрахлорид титана, а минимум находится на границе области).
В формуле (1) и далее U – вектор скорости, P – давление, T – температура, t – время, g – сила тяжести, χ – коэффициент температуропроводности, β – температурный коэффициент объемного расширения, ν – кинематическая вязкость, r – радиус цилиндра, Q – выделяемое тепло, ГTXT – верхняя поверхность цилиндра, Гохл – верхняя часть боковой поверхности цилиндра высотой hохл, на которой производится охлаждение, Гизол– нижняя часть боковой поверхности и основание цилиндра, которые являются теплоизолированными, SΓТХТ = πr2 – площадь верхней
поверхности цилиндра SΓохл = 2πrhохл – площадь охлаждаемой
части боковой поверхности.
Для реализации задачи использовался комплекс программ OpenFOAM Extend 3.1 с использованием сетки, построенной в программе Salome. Часть расчетов выполнялась на суперкомпьютере «Тритон» ИМСС УрО РАН. Уравнения (1) в рамках пакета OpenFOAM Extend 3.1 решаются с помощью метода контрольного объема [4].
Параметры конечно-разностной сетки для двумерного случая: 250× 75 , 500 ×150 ячеек. Для трехмерных расчетов использовалась блочная регулярная сетка с общим количеством
250 000 ячеек.
В работе был рассмотрен диапазон числа Грасгофа в пределах от 106 до 1010. Показано что при значении числа Грасгофа не выше Gr = 2·107 течение остается стационарным и осесимметричным, и в верхней части реторты возникает кольцевой вихрь. Однако при дальнейшем увеличении числа Грасгофа течение становится нестационарным, теряет осевую симметрию.
На рисунке представлены мгновенные поля скорости, полученные в результате расчетов в двухмерной и трехмерной постановке при Gr = 2,3 108 с числом Pr = 0,0087.
201
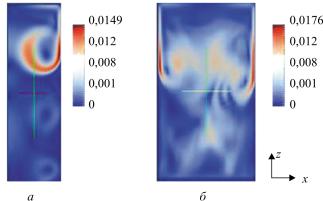
Рис. Поле скорости (в м/с)
На рисунке, а изображено поле скорости для двумерной осесимметричной постановки задачи, в этом случае расчетная область представляет собой прямоугольник с осью симметрии на левой боковой границе. На рисунке, б представлено поперечное сечение цилиндра из трехмерного расчета, ось цилиндра находится посередине рисунка. Для данного режима с числом Грасгофа Gr = 2,3·108 мгновенные поля скорости в двумерной и трехмерной постановке задачи отличаются. Следует отметить, что данный режим является существенно менее развитым, чем режимы, которые соответствуют реальному процессу восстановления титана.
При дальнейшем увеличении числа Грасгофа структура течения имеет ярко выраженный погранслойный характер, конвективные вихри занимают весь объем полости. Также с увеличением числа Gr в трехмерном случае скорость растет быстрее, чем в осесимметричном случае. Общий вид потоков становится более сложным. Также можно заметить, что вихрь смещается в сторону основания цилиндра.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 13-01- 96042_Урал).
202
Список литературы
1. Титан / В.А. Гармата, А.Н. Петрунько, Н.В. Галицкий
[и др.]. – М.: Металлургия, 1983. – 559 с.
2. Зимин В.Д., Ляхов Ю.Н., Сорокин М.П. Конвекция в вертикальном цилиндре при подогреве сверху // Гидродинамика: сб. ст. – Пермь, 1975. – Вып. VI. – С. 73–84. (Ученые Записки Перм. ун-та. № 327).
3.Гершуни Г.З., Жуховицкий Е.М., Непомнящий А.А. Устойчивость конвективных течений. – М.: Наука, 1989.
4.Jasak H. Error analysis and estimation for the finite volume method with applications to fluidflows. – 1996. – 394 р.
ОПТИМИЗАЦИЯ ДВУХЛИСТОВОГО УПРУГОГО ЭЛЕМЕНТА С ШАРНИРОМ И БЕЗ ШАРНИРА
А.А. Касаткин, М.А. Осипенко, Ю.И. Няшин
(Пермский национальный исследовательский политехнический университет,
Пермь, Россия, 79519531265@yandex.ru)
Рассмотрено несколько задач оптимизации двухлистового упругого элемента. Нижний лист имеет постоянный профиль, а верхний – линейный профиль. В одном случае оба листа считались консольно закрепленными балками Бернули–Эйлера, в другом нижний лист оснащен шарниром вместо жесткой заделки. Оптимизация состояла в отыскании толщины нижнего листа, длины и параметров профиля верхнего листа, минимизирующих напряжения в упругом элементе при заданных жесткости и общем размере.
Ключевые слова: упругий элемент, двухлистовая рессора, контактная задача, равнонапряженный упругий элемент, оптимизация.
Листовые рессоры широко используются в качестве упругих элементов подвесок автомобилей и других транспортных средств [1]. Известно также их использование в качестве упругого элемента протеза стопы [2]. Контактные задачи рас-
203

чета статического изгиба и оптимизации таких рессор по этой причине являются актуальными. Несмотря на то что эти задачи в настоящее время активно изучаются, имеется лишь весьма небольшой набор решений для отдельных задач [2, 3]. Причина этого состоит в том, что даже при использовании простейшей теории изгиба одного листа задача о совместном изгибе листов является контактной. Численные методы решения контактных задач [4] в данном случае требуют значительной адаптации.
В данной работе модель рессоры и постановка контактной задачи соответствуют схеме, принятой в работах [2, 3, 5, 6]. Каждый лист представляет собой консольно закрепленную прямолинейную балку (кроме случая, когда балка вместо жесткой заделки оснащена шарниром), испытывающую слабый изгиб в одной плоскости; нагрузка – сила, сосредоточенная на свободном конце длинного листа (рисунок). Листы имеют различные, вообще говоря переменные, толщины. В отсутствие нагрузки листы плотно прилегают друг к другу; трением пренебрегаем. Изгиб каждого листа описывается моделью Бернулли–Эйлера. Задача заключается в отыскании линий изгиба листов и сводится к отысканию плотности сил взаимодействия листов.
Рис. Модели двухлистовой рессоры с листом линейного профиля: а – оба листа консольно закреплены; б – верхний лист консольно закреплен, нижний оснащен шарниром
В общем случае построен численный метод решения контактной задачи, основанный на итерационном уточнении области контакта.
204
Построенный численный метод позволяет решать задачи оптимизации конструкции двухлистового упругого элемента. Оптимизация состоит в отыскании параметров конструкции (толщина нижнего листа, длина и параметры профиля верхнего листа), минимизирующих максимальное напряжение при заданных размере (длина нижнего листа) и прогибе. Найдены параметры оптимальной конструкции двухлистового упругого элемента с длинным листом постоянного профиля и коротким листом линейного профиля. В первом случае оба листа считаются консольно закрепленными балками, во втором вместо жесткой заделки нижний лист оснащен шарниром. Оптимальные параметры найдены сначала численно, а затем существенно уточнены посредством аналитических расчетов. Показано, что оптимальным упругим элементом является равнонапряженный, но не каждый равнонапряженный является оптимальным.
Список литературы
1.Пархиловский И.Г. Автомобильные листовые рессоры. – М.: Машиностроение, 1978. – 232 с.
2.Mathematical modelling of the foot prosthesis elastic element under bending / M.A. Osipenko, Y.I. Nyashin, R.N. Rudakov, A.V. Ostanin, E.N. Kuleshova, T.N. Zhuravleva // Russian Journal of Biomechanics. – 2001. – Vol. 5, № 2 – P. 18–29.
3.Осипенко М.А., Няшин Ю.И. Об одном подходе к решению некоторых одномерных контактных задач // Известия Сарат. ун-та. Новая серия. – 2011. – Т. 11. – Сер.: Математика. Механика. Информатика. – Вып. 1. – С. 77–84.
4.Li H., Dempsey J.P. Unbonded Contact of Finite Timoshenko Beam on Elastic Layer // Journal of Engineering Mechanics. – 1988. – July, Vol. 114, № 7. – P. 1265–1284.
5.Осипенко М.А., Няшин Ю.И., Касаткин А.А. Особенности контактных задач для систем струн и балок со слабо закрепленными элементами // Вестник Пермского национального исследовательского политехнического университета.
205
Механика. – 2015. – № 1. – С. 121–129. DOI: 10.15593/perm. mech/2015.1.08
6. Осипенко М.А. Контактная задача об изгибе двухлистовой рессоры с листами, искривленными по дуге окружности // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2014. – № 1. – С. 142–152.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ КАПЛИ В НЕОДНОРОДНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ
М.А. Кашина
(Пермский государственный национальный исследовательский университет,
Пермь, Россия, alabuzhev@mail.ru)
Исследуются вынужденные колебания капли жидкости в переменном неоднородном электрическом поле. В равновесном состоянии капля имеет форму цилиндра, равновесный краевой угол прямой. Капля окружена другой жидкостью и ограничена в осевом направлении параллельными твердыми диэлектрическими плоскостями. Для описания движения контактной линии используется эффективное граничное условие: скорость движения контактной линии пропорциональна сумме отклонения краевого угла и скорости быстрых релаксационных процессов, частоты которых пропорциональны частоте электрического поля.
Ключевые слова: электросмачивание, капля жидкости, вынужденные колебания, электрическое поле.
Данная работа посвящена продолжению исследований колебаний цилиндрической капли в переменном электрическом поле, которое играет роль внешней силы, заставляя двигаться линию контакта [1–3]. Интерес к этой теме обусловлен не только наличием разнообразных эффектов, но и технологическими причинами. Изменение свойств подложки, по которой движется капля, с помощью электрического поля (электросмачивание) является одним из перспективных методов управления такими объектами [4].
206
Для описания движения контактной линии используется модифицированное условие Хокинга [5–7]: скорость движения контактной линии пропорциональна сумме отклонения краевого угла и скорости быстрых релаксационных процессов, частоты которых пропорциональны частоте электрического поля:
∂ζ = ±Λ |
∂ζ |
+ Af (α)cos (2ωt ) |
, |
|
∂t |
|
∂z |
|
|
где z – ось симметрии капли; α – полярный угол; Λ – постоянная Хокинга; A – амплитуда колебаний. Случай однородного электрического поля рассматривался в работах [1, 2].
Вданной работе исследуется влияние переменного электрического поля на устойчивость вынужденных колебаний капли жидкости. В равновесном состоянии капля имеет форму цилиндра, ограниченного в осевом направлении параллельными твердыми плоскостями. Равновесный краевой угол – прямой. Капля окружена несжимаемой жидкостью другой плотности. Собственные колебания такой капли рассмотрены в работе [8]. Экспериментально подобная конфигурация исследовалась, например, в работе [9].
Вкачестве примера рассмотрим неоднородный периодический потенциал электрического поля вдоль оси x:
∞
f (α) = sin (κ cos (α)) = cncos ((2n + 1)α),
n=0
где κ – волновое число; cn – коэффициенты разложения в ряд Фурье. На рис. 1 показаны значения cn для трех значений κ.
Решение искалось в виде ряда по собственных функциям оператора Лапласа для цилиндрической системы координат. На рис. 2 показана зависимость безразмерной амплитуды отклонения лини контакта и краевого угла от частоты электрического поля для разных значений постоянной Хокинга. Отметим, что ρi – безразмерная плотности капли; ρc = 1 – ρi – безразмерная плотность
207

Рис. 1. Значения коэффициентов разложения пространственной неоднородности: а – κ = 1; б – κ = 10; г – κ = 100
Рис. 2. Максимальное отклонение поверхности (а, в) от равновесного значения и краевого угла (б, г)
в зависимости от частоты ω (κ = 1; ρi = 0,7; a = 2,5; b = 1): а, б – λ = 0,1 – сплошная линия, λ = 1 – штриховая; в, г – λ = 10 – штриховая, λ = 100 – пунктирная
208
внешней жидкости; b – геометрический параметр, равный отношению высоты капли к ее равновесному радиусу. Из приведенных рисунков видно, что при малых λ амплитуда отлична от нуля только вблизи резонансных значений частот. Существуют так называемые «антирезонансные» частоты [10, 11], когда контактная линия неподвижна при любых значениях λ.
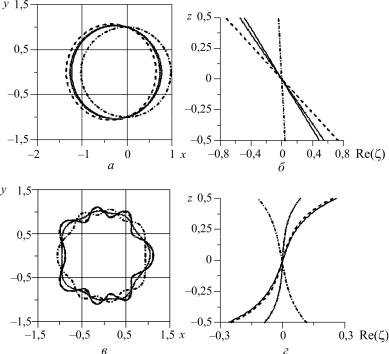
На рис. 3 показана форма линии контакта и боковой поверхности в разные моментыпериодаколебаний. Пространственная
Рис. 3. Форма контактной линии (а, в) и отклонения боковой поверхности (б, г) в различные моменты периода колебаний T
(ρi = 0,7, a = 2,5, b = 1): а, б – κ = 1; в, г – κ = 10, t = 0 – сплошная линия, t = T/8 – штриховая, t = T/4 – пунктирная,
t = 3T/8 – штрихпунктирная
209
неоднородность при κ = 1 возбуждает трансляционную моду колебаний (см. рис. 2, a; 3, а) и решения ~ cos(α). Отклонение боковой поверхности ~ z (рис. 3, б). При κ = 10 возбуждаются моды с более высокими азимутальными числами (рис. 3, в) и вдоль боковой поверхности распространяетсябегущаяволна (рис. 3, г).
Работа выполнена при финансовой поддержке проекта Российского научного фонда № 14-21-00090.
Список литературы
1.Кашина М.А. Влияние переменного электрического поля на колебания цилиндрической капли // Математическое моделирование в естественных науках. – 2014. – Т. 1. – С. 120–122.
2.Алабужев А.А., Кашина М.А. Колебания цилиндрической капли в переменном электрическом поле // Технические науки – от теории кпрактике. – 2014. – № 41. – С. 124–128.
3.Кашина М.А., Алабужев А.А. Вынужденные колебания цилиндрической капли в переменном неоднородном электрическом поле // XIХ Зимняя школа по механике сплошных сред:
сб. ст. / отв. ред. Н.А. Юрлова. – Пермь, 2015. – С. 105–110.
4.Mugele F., Baret J.-C. Electrowetting: from basics to applications // J. Phys.: Condens. Matter. – 2005. – Vol. 17. – P. 705–774.
5.Hocking L.M. The damping of capillary-gravity waves at a rigid boundary // J. Fluid Mech. – 1987. – Vol. 179. – P. 253–266.
6.Кайсина М.И. Азимутальные моды собственных колебаний цилиндрического пузырька // Вестник Перм. ун-та. Сер.: Математика. Механика. Информатика. – 2015. – №2 (29). – С. 37–45.
7.Любимов Д.В., Любимова Т.П., Шкляев С.В. Неосесимметричные колебания полусферической капли // Известия РАН. Механика жидкости и газа. – 2004. – № 6. – С. 8–20.
8.Алабужев А.А., Любимов Д.В. Влияние динамики контактной линии на собственные колебания цилиндрической кап-
ли // ПМТФ. – 2007. – Т. 48, № 5. – С. 78–86.
210
