
644_Galkina_M.JU._Vychislitel'naja_matematika_
.pdfФедеральное агентство связи
Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет телекоммуникаций и информатики» (СибГУТИ)
М. Ю. Галкина
Вычислительная математика
Практикум
Новосибирск
2016
1
УДК 519.6 (075.8)
Утверждено редакционно-издательским советом СибГУТИ
Рецензент доц. Т.Э. Захарова
Галкина М.Ю. Вычислительная математика: Практикум / Сибирский государственный университет телекоммуникаций и информатики. – Новосибирск, 2016. – 41 с.
В практикуме содержатся 5 лабораторных и курсовая работа для самостоятельного выполнения студентами. К каждой работе имеются методические указания по выполнению.
Пособие предназначено для студентов заочной формы обучения, обучающихся по направлению 09.03.01 «Информатика и вычислительная техника» и изучающих дисциплину «Вычислительная математика».
В авторской редакции
©Галкина М.Ю., 2016
©Сибирский государственный университет телекоммуникаций и информатики, 2016
|
ОГЛАВЛЕНИЕ |
|
1. |
ИНТЕРПОЛЯЦИЯ............................................................................................. |
4 |
1.1. |
Задача интерполяции...................................................................................... |
4 |
1.2. |
Интерполяционный многочлен Лагранжа..................................................... |
4 |
1.3. |
Интерполяционный многочлен Ньютона...................................................... |
6 |
1.4. Линейная и квадратичная интерполяция....................................................... |
9 |
|
1.5. Задание на лабораторную работу №1.......................................................... |
11 |
|
1.6. Методические указания к выполнению лабораторной работы №1 ........... |
11 |
|
2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ ...................................... |
12 |
|
2.1. Прямые и итерационные методы................................................................. |
12 |
|
2.2. |
Норма матрицы и вектора ........................................................................... |
13 |
2.3. |
Метод простой итерации.............................................................................. |
14 |
2.4. |
Метод Зейделя............................................................................................... |
18 |
2.5. Задание на лабораторную работу №2.......................................................... |
20 |
|
2.6. Методические указания к выполнению лабораторной работы №2 ........... |
20 |
|
3. |
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ .................................................. |
21 |
3.1. |
Общие замечания......................................................................................... |
21 |
3.2. Метод деления пополам (метод бисекции) ................................................. |
22 |
|
3.3. |
Метод хорд.................................................................................................... |
23 |
3.4. |
Метод касательных (метод Ньютона).......................................................... |
24 |
3.5. Задание на лабораторную работу №3.......................................................... |
25 |
|
3.6. Методические указания к выполнению лабораторной работы №3 ........... |
26 |
|
4. |
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ..................................................... |
26 |
4.1. |
Постановка задачи........................................................................................ |
26 |
4.2. Задание на лабораторную работу №4.......................................................... |
29 |
|
4.3. Методические указания к выполнению лабораторной работы №4 ........... |
30 |
|
5. |
ОДНОМЕРНАЯ ОПТИМИЗАЦИЯ ................................................................ |
30 |
5.1. |
Постановка задачи........................................................................................ |
30 |
5.2. |
Метод золотого сечения............................................................................... |
31 |
5.3. Задание на лабораторную работу №5.......................................................... |
33 |
|
6. |
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ.............................................................. |
33 |
6.1. |
Постановка задачи........................................................................................ |
33 |
6.2. |
Формула трапеций........................................................................................ |
34 |
6.3. |
Формула Симпсона....................................................................................... |
35 |
6.4. |
Метод двойного пересчета........................................................................... |
36 |
7. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ |
|
|
ПЕРВОГО ПОРЯДКА............................................................................................ |
36 |
|
7.1. |
Постановка задачи........................................................................................ |
36 |
7.2. |
Метод Эйлера................................................................................................ |
36 |
7.3. |
Методы Рунге-Кутта..................................................................................... |
37 |
7.4. |
Метод двойного пересчета........................................................................... |
38 |
8. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ........................................................... |
38 |
|
ЛИТЕРАТУРА........................................................................................................ |
40 |
|
3
1. ИНТЕРПОЛЯЦИЯ
1.1.Задача интерполяции
Пусть известны значения функции f в n + 1 различной точке х0, х1, х2… хn
(х0 < х1 < х2 < … < хп): у0 = f(х0), у1 = f(х1), … уn = f(хn). Например, эти значения найдены из эксперимента или найдены с помощью достаточно сложных вычислений. Возникает задача приближенно восстановить функцию f в произвольной точке x. Для решения такой задачи строится алгебраический многочлен Ln(x)
степени n, который в точках xi принимает те же значения yi, что и функция f(x), т.е.
Ln(xi) f (xi), i 0,1,2, n. (1)
Такой многочлен называется интерполяционным. Точки xi (i = 1, 2, n) на-
зываются узлами интерполяции.
Интерполяционный многочлен может строиться с использованием всех узлов интерполяции, тогда говорят о глобальной интерполяции. Если интерполяционные многочлены строятся отдельно для разных интервалов изменения x, то в этом случае имеем кусочную или локальную интерполяцию. Как правило, интерполяционные многочлены используются для нахождения значений функции в промежуточных точках между крайними узлами интерполяции, т.е. при x ( x0, xn). Но иногда эти многочлены используются для вычисления значений функции вне отрезка (x0, xn). Такое приближение называют экстраполяцией.
1.2.Интерполяционный многочлен Лагранжа
Будем искать многочлен в виде линейной комбинации многочленов степени n:
Ln(x) y0 pi(x) y1 p1(x) yn pn(x). |
(2) |
При этом потребуем, чтобы каждый многочлен pi(x) обращался в нуль во всех узлах интерполяции, за исключением одного i-го узла, где он должен равняться единице. Легко проверить, что этим условиям отвечает многочлен вида
p (x) |
|
(x x0) (x xi 1)(x xi 1) (x xn) |
. |
(3) |
||||||||
|
|
|||||||||||
i |
(xi x0) (xi xi 1)(xi xi 1) (xi xn) |
|
||||||||||
|
|
|||||||||||
Подставляя (3) в (2), находим, что |
|
|
|
|
|
|
|
|||||
n |
|
(x x0) (x xi 1)(x xi 1) (x xn) |
|
|||||||||
Ln(x) yi |
(4) |
|||||||||||
|
|
|
|
|
|
. |
||||||
(x x |
) (x |
x |
)(x x |
) (x |
x ) |
|||||||
i 0 |
|
i |
0 |
i |
i 1 |
i i 1 |
i |
n |
|
|||
Интерполяционный многочлен, представленный в виде (4), называется ин-
терполяционным многочленом Лагранжа, а функции pi(x), представленные в виде (3) – лагранжевыми коэффициентами.
Можно доказать, что многочлен Лагранжа единственен. При n = 1 (интерполируем по двум точкам)
L (x) y |
|
x x1 |
y |
|
x x0 |
. |
(5) |
|||
|
|
|||||||||
1 |
0 |
|
x |
x |
1 |
|
x |
x |
|
|
|
|
|
0 |
1 |
|
1 |
0 |
|
|
|
При n = 2 (интерполируем по трем точкам)
4

L (x) y |
|
(x x1)(x |
x2) |
y |
|
(x |
x0)(x x2) |
y |
2 |
|
(x x0)(x x1) |
. (6) |
||||||||||
(x x )(x |
|
(x |
|
|
||||||||||||||||||
2 |
0 |
|
|
x ) |
1 |
|
x )(x x |
2 |
) |
|
|
(x x )(x |
2 |
x ) |
|
|||||||
|
|
|
0 |
1 |
0 |
2 |
|
1 |
0 |
1 |
|
|
|
|
2 |
0 |
1 |
|
||||
Пример 1
Построить интерполяционный многочлен Лагранжа по заданной таблице значений функции и с его помощью приближенно найти f(4).
|
xi |
0 |
2 |
3 |
5 |
|
f(xi) |
1 |
3 |
2 |
5 |
Согласно (4) при n = 3 имеем |
|||||
L (x) 1 |
(x 2)(x 3)(x 5) |
3 |
(x 0)(x 3)(x 5) |
2 |
(x 0)(x 2)(x 5) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3 |
|
|
|
(0 2)(0 3)(0 5) |
|
(2 0)(2 3)(2 5) |
|
(3 0)(3 2)(3 5) |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
5 |
(x 0)(x 2)(x 3) |
|
|
3 |
x3 |
13 |
x2 |
62 |
x 1, |
|
|
|
||||||||||||
(5 0)(5 2)(5 3) |
|
|
|
|
|
|
|
|||||||||||||||||
|
10 |
|
|
16 |
15 |
|
|
|
|
|||||||||||||||
3 |
|
3 |
13 |
|
2 |
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
|||||
f (4) |
|
|
4 |
|
|
4 |
|
|
|
|
|
4 1 2.067. |
|
|
|
|||||||||
|
|
|
15 |
|
|
|
||||||||||||||||||
10 |
|
|
16 |
|
|
|
|
|
|
|
|
f (x) Ln(x) Rусеч(x), где Rусеч – погрешность |
||||||||||||
|
Можно записать равенство |
|
||||||||||||||||||||||
усечения, возникающая из-за замены функции на интерполяционный многочлен. Если относительно f ничего не известно, кроме значений в узлах интерполяции, то никаких суждений относительно Rусеч сделать нельзя. Если имеется оценка сверху для (n + 1)-ой производной f(x) на интервале (x0, xn):
M |
n 1 |
max |
f (n 1)(x) |
,где |
x [x ,x ], то можно получить оценку максимальной |
|
|
|
|
|
0 |
n |
|
погрешности интерполяции на всем отрезке [x0, xn]:
R |
(x) |
Mn 1 |
|
|
(x x |
)(x x )...(x x |
n |
) |
|
. |
|
|
|
|
|||||||||
|
|||||||||||
усеч |
|
(n 1)! |
|
0 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Пример 2
Оценить погрешность приближения функции f (x) 
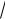 x в точке x = 116 с помощью интерполяционного многочлена Лагранжа, построенного с узлами x0=100, x1=121, x2=144.
x в точке x = 116 с помощью интерполяционного многочлена Лагранжа, построенного с узлами x0=100, x1=121, x2=144.
По формуле (6) имеем
L (116) 10 |
(116 |
121)(116 144) |
11 |
(116 |
100)(116 144) |
|
|
|
|
||
2 |
(100 |
121)(100 144) |
(121 |
100)(121 144) |
|
|
|||||
12 (116 121)(116 100) 10.7694. (144 100)(144 121)
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
5 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
3 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f |
|
|
|
|
|
|
|
|
|
, |
|
f |
|
|
|
|
|
|
|
|
x , |
f |
|
|
x |
|
|
x , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
(x) ( |
|
x) |
2 x |
|
(x) |
|
|
(x) |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
|
4 |
|
|
|
|
|
|
4 |
|
|
8 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M3 |
max |
|
|
3 |
|
|
1 |
|
|
|
|
3 |
|
1 |
|
|
|
3 |
10 |
5 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
8 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x5 |
|
|
|
1005 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x [100,144] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Rусеч M3 (116 100)(116 121)(116 144) 3!
1 10 5 16 5 28 1.4 10 3 2 10 3. 16
Если значения функции в узлах интерполяции заданы с погрешностью, то при интерполяции возникает погрешность округления. Если Е – максимальная погрешность одного вычисления f(xi), то при n >1 погрешность округления
можно оценить по формуле: Rокруг E (2n 1). Тогда полная погрешность интерполяции R Rусеч Rокруг.
1.3.Интерполяционный многочлен Ньютона
До сих пор не делалось никаких предположений о законе распределения узлов интерполяции. Сейчас рассмотрим случай равноотстоящих узлов, т.е. xi xi 1 h const, i 1,2, ,n. Величина h называется шагом интерполяции.
Введем понятие конечных разностей. Составим разности значений функции: y0 y1 y0, y1 y2 y1, , yn 1 yn yn 1. Эти значения называются
разностями первого порядка. Можно составить разности второго порядка
2y0 y1 y0, 2y1 y2 y1, . Аналогично составляются разности k-го
порядка k y |
k 1y |
k 1y , |
i 0,1, ,n 1. |
0 |
1 |
0 |
|
Конечные разности в точках xi удобно вычислять с помощью таблицы конечных разностей.
Пример 3
Найти конечные разности для функции f(x)=2x3–2x2+3x–1, x0 = 0, h = 1, i = 0, 1, 2, 3, 4.
x |
y |
y |
2y |
3y |
4y |
0 |
-1 |
3 |
8 |
12 |
0 |
1 |
2 |
11 |
20 |
12 |
|
2 |
13 |
31 |
32 |
|
|
3 |
44 |
63 |
|
|
|
4 |
107 |
|
|
|
|
Конечные разности можно выразить непосредственно через значения функции. Например,
6

2y0 y1 y0 (y2 y1) (y1 y0) y2 2y1 y0,
3y0 2y1 2y0 (y3 2y2 y1) (y2 2y1 y0) y3 3y2 3y1 y0.
Для любого k можно получить формулу:
k y |
y |
k |
ky |
k 1 |
|
k(k 1) |
y |
k 2 |
( 1)k y . |
(7) |
|
||||||||||
0 |
|
|
2! |
|
0 |
|
||||
Аналогичная формула имеет место для значения разности в узле xi:
k y |
y |
k i |
ky |
k i 1 |
|
k(k 1) |
y |
k i 2 |
( 1)k y . |
(8) |
|
||||||||||
i |
|
|
2! |
|
ii |
|
||||
Можно определить значение yk, используя конечные разности:
y |
k |
y |
k y |
0 |
|
k(k 1) |
|
2y |
k y . |
(9) |
|
||||||||||
|
0 |
|
2! |
|
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
||
Перейдем к построению интерполяционного многочлена Ньютона. Будем искать его в виде:
Nn(x) a0 a1(x x0) a2(x x0)(x x1) |
|
|
|
an(x x0)(x x1) (x xn 1). |
(10) |
График функции |
должен проходить через заданные узлы, |
т.е. |
Nn(xi) yi (i 0,1,2, n). |
Следовательно, из этих условий получаем систему |
|
для нахождения коэффициентов многочлена:
Nn(x0) a0 y0,
Nn(x1) a0 a1(x1 x0) a0 a1h y1,
Nn(x2) a0 a1(x2 x0) a2(x2 x0)(x2 x1) a0 2a1h 2a2h2 y2,
……………………………………………………
Nn(xn) a0 a1(xn x0) a2(xn x0)(xn x1) an(xn x0)(xn x1) (xn xn 1).
Найдем неизвестные коэффициенты:
a y |
0 |
, |
a |
y1 a0 |
|
y1 y0 |
|
y0 |
, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
|
|
1 |
h |
|
|
h |
|
|
h |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2y |
|
|
||||||||
|
|
|
y |
2 |
a 2a h |
y |
2 |
y |
0 |
2 y |
0 |
|
||||||||||
a |
2 |
|
|
|
0 |
1 |
|
|
|
|
|
|
0 |
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
h2 |
|
|
|
|
|
2h2 |
2h2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Аналогично можно найти и остальные коэффициенты. Общая формула для коэффициента ak имеет следующий вид:
ak k y0 , k 0,1,2, ,n. k!hk
Подставляя выражения для ak в формулу (10), находим интерполяционный многочлен Ньютона:
|
|
|
|
|
|
y |
2y |
|
|
|
||
N |
n |
(x) y |
|
|
|
0 |
(x x ) |
0 |
(x x )(x x ) |
|||
|
h |
|
2!h2 |
|||||||||
|
ny |
0 |
|
0 |
|
0 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
(x x |
)(x x ) (x x |
|
) |
(11) |
||||||
|
|
|||||||||||
|
|
n!hn2 |
|
|
0 |
1 |
n 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Конечные разности могут быть вычислены по формуле (7).
7

Формулу (11) часто записывают в другом виде. Для этого вводится пере-
менная q |
x x0 |
, |
тогда |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x qh, |
|
x x1 |
|
x x0 h |
q 1, |
x x2 |
q 2, , |
x xn 1 |
|
q n 1. |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
h |
|
|
|
h |
|
h |
|
h |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
С учетом этих соотношений формулу (11) можно переписать в виде: |
|
||||||||||||||||||
N |
n |
(x) y q y |
0 |
|
q(q 1) |
2y |
q(q 1) (q n 1) |
ny . |
(12) |
||||||||||
|
|
||||||||||||||||||
|
|
0 |
|
|
|
2! |
|
0 |
|
|
n! |
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полученное выражение носит название первого интерполяционного много-
члена Ньютона для интерполяции вперед. Эту формулу используют для вычис-
ления значений функции в точках левой половины отрезка (x0, xn) и для экстраполяции левее x0. Для правой половины отрезка (x0, xn) разности лучше
вычислять справа налево, поэтому вводят переменную q x x0 , т.е. q < 0 и
|
|
|
h |
|
интерполяционный многочлен Ньютона можно получить в виде |
||||
Nn(x) yn q yn |
q(q 1) |
2yn |
q(q 1) (q n 1) |
nyn. (13) |
|
|
|||
2! |
|
n! |
||
Полученная формула называется вторым интерполяционным многочленом Ньютона для интерполяции назад. Формула (13) используется также для экстраполяции правее xn.
Если имеется дополнительный узел xn+1, то погрешность первого интерполяционного многочлена Ньютона можно оценить по формуле:
R (x) |
|
q(q 1) (q n) |
|
n 1y |
0 |
, гдеq |
x x0 |
. |
(14) |
|
|
||||||||
усеч |
|
(n 1)! |
|
|
|
h |
|
||
|
|
|
|
|
|
|
|||
Следует подчеркнуть, что существует один и только один интерполяционный многочлен при заданном наборе узлов интерполяции. Формулы Лагранжа и Ньютона порождают один и тот же многочлен. Разница лишь в алгоритме их построения. Выбор способа интерполяции определяется различными соображениями: точностью, временем вычислений, погрешностью округлений и др. В некоторых случаях предпочтительней может оказаться локальная интерполяция.
Достоинство многочлена Лагранжа в том, что он применим всегда, а не только для равностоящих узлов интерполяции, но суммирование при построении такого многочлена нельзя прерывать раньше времени. При использовании интерполяционного многочлена Ньютона суммирование можно прервать раньше времени, тогда получим интерполяционный многочлен более низкой степени, чем n.
Пример 4
Составить таблицу значений функции f(x) = 2x3 – 2x2 + 3x – 1 на интервале [0; 4] с шагом h = 1. По составленной таблице построить интерполяционный многочлен Ньютона и найти f (0.5).
x0 = 0, h = 1, i = 0, 1, 2, 3, 4.
8
Используя таблицу конечных разностей из примера 1 и формулу (12), получаем (точка 0.5 лежит в левой половине отрезка [0, 4]):
N |
4 |
(x) y |
|
q y |
0 |
|
q(q 1) |
2y |
0 |
|
q(q 1)(q 2) |
3y |
0 |
1 q 3 |
q(q 1) |
8 |
||||
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
2! |
|
3! |
|
|
2 |
|
|||||||||
|
q(q 1)(q 2) |
|
|
|
|
|
|
|
|
|||||||||||
|
12 1 3q 4q(q 1) 2q(q 1)(q 2), |
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
x x0 |
|
0.5 |
0 |
0.5. Тогда приближенное значение функции |
|
|
|||||||||||||
h |
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f (0.5) 1 3 0.5 4 0.5 (0.5 1) 2 0.5 (0.5 1) (0.5 2) 0.25.
1.4.Линейная и квадратичная интерполяция
Если x [xi, xi+1], то при n = 1 из формулы (12) получаем формулу линейной интерполяции:
f (x) N |
(x) y |
q y , |
q |
x xi |
. |
(15) |
|
||||||
1 |
i |
i |
|
h |
|
|
|
|
|
|
|
||
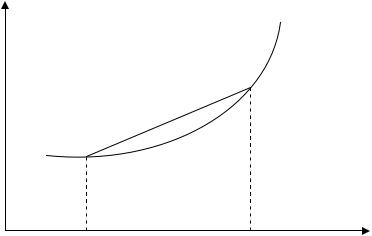
Геометрически линейная интерполяция означает замену графика функции на отрезке [xi, xi+1] хордой, соединяющей точки (xi, fi) и (xi+1, fi+1) (рис.1).
y
y= N1 (x)
y=f (x)
f (xi) f (xi+1)
xi |
xi+1 |
x |
Рис. 1. Линейная интерполяция Погрешность формулы (15) определяется неравенством:
|
M2h2 |
|
|
(16) |
|
| Rусеч(x)| |
, где M2 max | f |
||||
(x)|. |
|||||
8 |
[xi,xi 1] |
|
|
||
Если x [xi, xi+1], при n = 2 из формулы (12) получаем формулу квадратичной интерполяции (для интерполяции используем точки xi, xi+1, xi+2):
f (x) N |
2 |
(x) y |
q y |
|
q(q 1) |
|
2y , |
q |
x xi |
. |
(17) |
|
|
||||||||||
|
i |
i |
2! |
|
i |
|
h |
|
|||
|
|
|
|
|
|
|
|
||||
Если для интерполяции используем точки xi-1, xi, xi+1, то получаем форму-
лу:
f (x) N |
2 |
(x) y |
q y |
|
q(q 1) |
2y , |
q |
x xi 1 |
. |
(18) |
|
|
|||||||||
|
i 1 |
i 1 |
2! |
i 1 |
|
h |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
9 |
|
|
|
|
|
|
В первом случае квадратичная интерполяция геометрически означает замену графика функции на отрезке [xi, xi+2] параболой, проходящей через точки (xi, fi), (xi+1, fi+1) и (xi+2, fi+2). Во втором случае парабола проходит через точки
(xi-1, fi-1), (xi, fi) и (xi+1, fi+1).
Погрешность формулы (17) определяется неравенством:
|
M h3 |
|
|
|
|
| Rусеч(x)| |
3 |
, |
где M3 max | f |
|
(19) |
|
|||||
16 |
(x)|. |
||||
|
|
[xi,xi 2] |
|
|
|
Для формулы (18) оценка погрешности та же самая, только в этом случае |
|||||
M3 |
|
max |
| f |
|
|
(x)|. |
|||||
|
[x |
|
,x |
] |
|
|
i 1 |
i 1 |
|
|
|
Пример 5
Составить таблицу значений функции f(x) = 2x3 – 2x2 + 3x – 1 на интервале [0; 4] с шагом h = 1. По составленной таблице с помощью линейной интерполяции найти f (3.5), а с помощью квадратичной интерполяции найти f (1.5). Оцените погрешности приближенных вычислений.
Используя таблицу конечных разностей из примера 3 п.1.2 и формулу (15), получаем формулу линейной интерполяции (точка x = 3.5 лежит между точка-
ми x3 = 3 и x4 = 4):
f (x) y q y |
44 63q, где q |
x x3 |
|
3.5 3 |
0.5. |
||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
3 |
|
3 |
|
|
|
|
|
|
h |
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Тогда приближенное значение функции |
f (3.5) 44 63 0.5 75.5. |
||||||||||||||||||
|
|
Оценим погрешность вычисления по формуле (16): |
|||||||||||||||||||
|
|
|
3 |
|
2x |
2 |
|
|
|
2 |
4x 3, |
|
|
|
|
|
|
|
2 |
|
|
f (x) (2x |
|
|
|
3x 1) 6x |
|
|
f (x) (6x |
|
4x 3) 12x 4, |
||||||||||||
M |
2 |
max |
|
|
12x 4 |
|
12 4 4 44,| R |
(x)| |
|
44 12 |
5.5. |
||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
x [3,4] |
|
|
|
|
|
|
|
|
усеч |
|
|
|
8 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Точка x = 1.5 лежит между точками x1 = 1 и x2 = 2, поэтому квадратичную интерполяцию можно делать по точкам x0, x1, x2 или x1, x2, x3. Выберем второй вариант. Используя таблицу конечных разностей из примера 3 п.1.2 и формулу (17), получаем формулу квадратичной интерполяции:
f (x) y q y |
q(q 1) |
2y 2 q 11 |
q(q 1) |
20 2 q 11 10q(q 1), |
||||||||
|
|
|
||||||||||
|
1 |
|
1 |
2! |
|
1 |
2 |
|
||||
|
|
x x1 |
|
|
|
|
|
|||||
где q |
|
1.5 1 |
0.5. Тогда приближенное значение функции: |
|||||||||
h |
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|||
f (x) 2 0.5 11 10 0.5 (0.5 1) 5. |
|
|
||||||||||
|
Оценим погрешность вычисления по формуле (19): |
|||||||||||
|
|
|
12, M3 |
12, |
|
|
||||||
f |
(x) (12x 4) |
|
|
|||||||||
| R |
(x)| |
12 13 |
0.75. |
|
|
|
||||||
|
|
|
|
|||||||||
усеч |
16 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
10
