644_Galkina_M.JU._Vychislitel'naja_matematika_

Для метода простой итерации погрешность оценивается по формуле

C k 1

R b .

1 C

По условию точность должна быть меньше, чем 0.01. Получаем,

R0.8k 1 1.2 0.01, 1 0.8

R 0.8k 1 1.2 0.01, 0.2

0.8k 1 0.0017, ln(0.8k 1) ln(0.0017),

(k 1) ln0.8 ln(0.0017),

k 1 ln(0.0017), ln(0.8)

k 1 28.6, k 28.

Выполнение 28 шагов по методу простой итерации гарантирует вычисление значения каждого неизвестного с точностью 0.01. При работе программы обычно получается меньшее количество шагов.

3. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

3.1.Общие замечания

Будем искать решение уравнения f (х) = 0, где f (x) – некоторая непрерывная нелинейная функция. Нелинейные уравнения можно разделить на два класса: алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции: целые, рациональные, иррациональные. В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие тригонометрические, показательные, логарифмические и другие неалгебраические функции, называются

трансцендентными.

Методы решения уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторой формулы. Однако на практике не всегда удается решить уравнения точными методами. Тогда используют итерационные методы, или методы последовательных приближений. Тогда процесс нахождения корня состоит из двух этапов:

отыскание приближенного значения корня или содержащего его отрезка

(интервала изоляции корня);

21

уточнение приближенного решения до некоторой заданной степени точности.

Приближенное значение корня (начальное приближение) может быть найдено различными способами: из физических соображений, из решения аналогичной задачи при других начальных данных, с помощью графических методов. Если такие оценки начального приближения произвести не удается, то находят две близко расположенные точки a и b, в которых непрерывная функция f (x) принимает значения разных знаков, т.е. выполняется условие: f (a) f (b) 0. В этом случае между точками a и b есть, по крайней мере, одна точка, в которой f (x) 0. В качестве начального приближения принимают одну из точек этого отрезка x0. Итерационный процесс состоит в нахождении последовательных приближений значений корня: x0, x1, xn. Если эти значения с ростом n приближаются к истинному значению корня, то итерационный про-

цесс сходится.

3.2.Метод деления пополам (метод бисекции)

Это один из простейших методов нахождения корней нелинейного уравнения. Пусть имеется интервал [а,b], на котором функция f (x) меняет свой знак, т.е. f (a) f (b)<0. В качестве начального приближения корня возьмем середину этого интервала: x0 = (a + b)/2. Далее выясняем, на каком из интервалов – [a, x0] или [x0,b] функция f меняет знак. В качестве нового интервала рассматриваем ту половину интервала [а,b], на которой происходит смена знака. В качестве нового приближения корня выбираем середину нового отрезка и т.д. Таким образом, после каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, т.е. после n итераций начальный интервал уменьшится в 2n раз. Итерационный процесс продолжается до тех пор, пока длина интервала изоляции корня не станет меньше заданной точности. В качестве приближенного значения корня принимаем середину последнего интервала.

Достоинством метода деления пополам является то, что он обязательно сходится, хотя и медленно. При этом

где x* - точное значение корня

Неравенство (32) позволяет оценить количество шагов n, необходимых для достижения заданной точности .

22

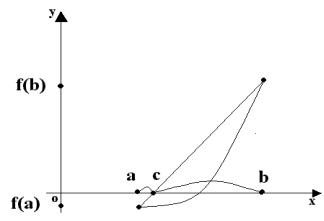
3.3.Метод хорд

Вметоде деления пополам интервал многократно делится пополам, а в методе хорд интервал делится на неравные части в отношении f (a): f (b).

Пусть имеется интервал [а,b], на котором функция f (x) меняет свой знак, т.е. f (a) f (b)<0. Для определенности будем считать, что f (a) 0, f (b) 0.

В методе хорд процесс итераций состоит в том, что в качестве последовательности приближений к корню принимаются значения точек пересечения хорды, соединяющей точки a и b с осью Ox (рис. 2).

B

A

Рис. 2. Метод хорд

Из отрезков [a,c] и [c,b] выбираем тот, на котором функция меняет знак. Для рассматриваемого случая это отрезок [с,b]. Следующая итерация состоит в определении нового приближения как точки пересечения новой хорды с осью Ox и т.д. Повторяем процесс до тех пор, пока не будет достигнута заданная точность.

Оценку скорости сходимости в методе хорд дает следующая теорема.

Теорема 3

Если на интервале [a,b] функция f (x) непрерывна и дифференцируема, а ее производная f (x) на интервале [a,b] имеет постоянный знак (т.е. на [a,b] функция f (x) монотонна), то верна следующая оценка:

23

Следствие

Если отрезок [a,b] достаточно узок, т.е. M1 2m1, то

В этом случае итерационный процесс продолжается до тех пор, пока не будет выполняться условие: xn xn 1 , где – заданная точность.

3.4.Метод касательных (метод Ньютона)

Метод касательных является наиболее употребительным при приближенном решении уравнений, т.к. дает довольно быструю сходимость процесса вычислений к нужному результату.

Процесс производимых итераций метода пояснен на рис. 3. Составим уравнение касательной в точке (xn, f (xn)). Поскольку угловой коэффициент ка-

Рис. 3. Метод Ньютона

Для точки пересечения касательной с осью Ox (x =xn+1, y =0) получаем

0 f (xn) f (xn) (xn 1 xn),

вверх или вниз), то погрешность метода Ньютона можно оценить по формуле:

Метод Ньютона обеспечивает эффект удвоения верных знаков после каждой итерации.

Следующая формула связывает погрешности двух последних приближений xn-1 и xn:

Иногда бывает затруднительно вычислять на каждом шаге f (xn). Если производная f (x) мало изменяется на отрезке [a,b], то в формуле Ньютона (36) можно положить f (xn) f (x0). Тогда получим формулу модифицированного метода Ньютона:

В этом случае касательные в точках (хn, f (xn)) заменяются прямыми, параллельными касательной в точке (х0, f (x0)). Модифицированный метод работает не хуже, чем метод Ньютона, но дает более медленную скорость сходимости.

3.5.Задание на лабораторную работу №3

Найти аналитически интервалы изоляции действительных корней нелинейного уравнения, для чего найти производную левой части уравнения и составить таблицу знаков левой части на всей числовой оси.

Написать программу нахождения всех действительных корней нелинейного уравнения методом деления пополам с точностью 0.0001. Считается, что требуемая точность достигнута, если выполняется условие | xn 1 xn | ,

( – заданная точность), при этом x xn xn 1 . 2

Номер варианта выбирается по последней цифре зачетной книжки.

Вариант 0: 2x3 3x2 12x 5 0. Вариант 1: x3 3x2 24x 3 0.

Вариант 2: x3 3x2 24x 10 0.

Вариант 3: 2x3 3x2 12x 10 0.

Вариант 4: x3 3x2 24x 10 0. Вариант 5: x3 3x2 24x 8 0. Вариант 6: 2x3 3x2 12x 1 0. Вариант 7: x3 3x2 24x 5 0. Вариант 8: x3 3x2 24x 1 0.

Вариант 9: 2x3 3x2 12x 12 0.

25

3.6.Методические указания к выполнению лабораторной работы №3

Составим таблицу знаков функции f (x):

x1 ]– ; –2/3[, x2 ]–2/3; 2[, x3 ]2; + [. Уменьшим промежутки, содержащие корни:

x1 ]–2; –2/3[, x2 ]–2/3; 2[, x3 ]2; 3[

4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ

4.1.Постановка задачи

Пусть имеется функция f (x), которую необходимо продифференцировать несколько раз и найти производную в некоторой точке.

Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно заменить его более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных вообще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования функции.

Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции заменяется соответствующей производной интерполяцион-

26

Воспользуемся формулой линейной интерполяции

Формула (43) носит название второй разностной производной.

Формулы (40) – (43) называются формулами численного дифференцирова-

ния.

При численном дифференцировании, как и при интерполяции, возникает два типа погрешностей: усечения и округления. Погрешность усечения возникает из-за замены функции на интерполирующий многочлен и ее производной на производную от интерполяционного многочлена. Погрешность округления

27

возникает из-за того, что значения уi известны не точно, а с некоторой погрешностью .

Оценим погрешность усечения. Предполагая функцию f достаточное число раз непрерывно дифференцируемой, можно получить погрешности усечения приближенных формул (40) – (43).

Для формулы (40):

Погрешности округления формул (40), (42), (43), соответственно равны

2 /h, /h,4 /h2.

Погрешность усечения при уменьшении h уменьшается, а погрешность округления, напротив, увеличивается (рис. 4). Поэтому шаг не следует брать слишком большим, чтобы погрешность усечения не была велика, и не следует брать слишком маленьким, чтобы не была велика погрешность округления.

y

Суммарная

погрешность

Рис. 4. Оптимальный шаг дифференцирования Оптимальный шаг для формулы (40):

Оптимальный шаг для формулы (42):

28

Пример 10

По таблице значений функции f (x) найти оценку первой производной в

Погрешность усечения оценим по формуле (45): Rусеч 0.12 2.5 0.005.

6

f (0.5) 5.425 0.005

Используя интерполяционные многочлены более высоких порядков, можно получать формулы численного дифференцирования для производных более высокого порядка и для бо́льшего количества узлов интерполирования.

4.2.Задание на лабораторную работу №4

Известно, что функция f (x) удовлетворяет условию | f (x)| c при любом x. Измерительный прибор позволяет находить значения f (x) с точностью 0.0001. Найти наименьшую погрешность, с которой f (x) можно найти по при-

ближенной формуле: f (xi) f (xi 1) f (xi 1) . Рассчитать шаг для построения

2h

таблицы значений функции, которая позволит вычислить значения f (x) с наименьшей погрешностью.

Составить программу, которая:

1.Выводит таблицу значений функции с рассчитанным шагом h на интер-

вале [c – h, c + 21h].

29

c 3 (0.1(N 1))3, N – последняя цифра зачетной книжки. Точное значение

производной f (x) 1 sin(cx). c

4.3.Методические указания к выполнению лабораторной работы №4

Рассмотрим пример расчета оптимального шага дифференцирования при