644_Galkina_M.JU._Vychislitel'naja_matematika_

1.5.Задание на лабораторную работу №1

Известно, что функция f (x) удовлетворяет условию | f (x)| 2c при любом x. Рассчитать шаг таблицы значений функции f(x), по которой с помощью линейной интерполяции можно было бы найти промежуточные значения функции с точностью 0.0001, если табличные значения функции округлены до 4-х знаков после запятой. Составить программу, которая:

1.Выводит таблицу значений функции с рассчитанным шагом h на интер-

вале [c, c+30h].

2.С помощью линейной интерполяции вычисляет значения функции в точ-

с шагом h.

3.Выводит значения xi, приближенные и точные значения функции в точках xi (i = 0,1, 29).

где N – последняя цифра зачетной книжки, i mod 4 – остаток от деления i на 4 (например, 10 mod 4 = 2, 15 mod 4 = 3, 8 mod 4 = 0).

1.6.Методические указания к выполнению лабораторной работы №1

Рассмотрим пример расчета шага интерполяционной таблицы.

Пусть f (x) 2c3 sin(x / c), c 10. Полная погрешность интерполяции

R = Rусеч + Rокруг, где Rусеч – погрешность формулы линейной интерполяции, Rокруг – погрешность, возникающая из-за подстановки в формулу линейной интерполяции приближенных значений функции.

Известно, что погрешность формулы линейной интерполяции оценивается по следующему неравенству:

(f) = 0.5 10-4. Тогда при подстановке этих приближенных значений в формулу линейной интерполяции возникает погрешность:

Rокруг = (1 – q) (f) + q (f) = (f) = 0.5 10-4. По условию, общая погрешность

R 0.0001. Получаем,

5h2 0.5 10 4 10 4, 2

h2 2 (10 4 0.5 10 4), 5

11

h2 0.00002, h 0.00447, h 0.004.

2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

2.1.Прямые и итерационные методы

Пусть имеется система линейных алгебраических уравнений с n неизвестными:

за В – вектор-столбец правых частей, за Х - вектор-столбец неизвестных, то

Решение системы (2) всегда существует и единственно, если det A 0, т.е.

матрица A – невырожденная.

Все методы решения систем линейных уравнений можно разбить на две группы:

Прямые, или точные, методы.

Итерационные, или приближенные, методы.

Прямые методы используют формулы для вычисления неизвестных. Они дают решение системы за конечное число арифметических операций. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса систем линейных уравнений. Наиболее известным из прямых методов решения систем линейных уравнений является метод Гаусса.

Вместе с тем прямые методы имеют и ряд недостатков. При решении таких задач на компьютере они требуют хранения в оперативной памяти сразу всей матрицы, поэтому при больших значениях n расходуется много места в памяти. Также прямые методы не учитывают структуру матрицы – при большом числе нулевых элементов эти элементы все равно хранятся в памяти и над ними выполняются арифметические операции. Существенным недостатком прямых методов является накапливание погрешности в процессе решения, поскольку все вычисления на компьютере производятся с ограниченным числом знаков, определяемым разрядностью компьютера, и вычисления на любом этапе используют результаты предыдущих операций. Особенно это опасно для больших систем

12

(n > 200) и для систем с близким к нулю определителем (плохо обусловленных систем).

Итерационные методы – это методы последовательных приближений решения. В них необходимо задать начальное приближение решения. После этого с помощью некоторого алгоритма проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение решения. Итерации проводятся до получения решения с заданной точностью. Алгоритмы решения линейных систем с использованием итерационных методов более сложные по сравнению с прямыми методами. При этом объем вычислений заранее определить сложно.

Тем не менее в ряде случаев итерационные методы предпочтительнее прямых. Они требуют хранения в памяти не всей матрицы системы. Погрешность в процессе вычислений не накапливается, т.к. точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений.

2.2.Норма матрицы и вектора

Условия сходимости итерационных методов связаны с понятиями норм матрицы и собственными числами матрицы.

Пусть А – матрица размером m n (матрица содержит m строк и n столбцов). Нормой матрицы называется неотрицательное число ||A||, обладающее следующими свойствами:

1.||A|| 0, причем ||A|| = 0 тогда и только тогда, когда все элементы матрицы А равны нулю;

2.|| A|| = | | ||A||, где - произвольное число;

3.||A + В|| ||A|| + ||В||;

4.||A В|| ||A|| ||В||;

Нормы матрицы можно вводить различными способами. Рассмотрим примеры трех легко вычисляемых норм:

1.Первая норма (1-норма)

A 1 max aij .

j i

2. Вторая норма (Евклидова норма, или 2-норма):

3.Бесконечная норма( -норма) :

A max aij .

i j

Введенные нормы удовлетворяют всем свойствам из определения нормы.

13

A max(1 2 3,4 5 6,7 8 9) max(6,15,24) 24.

Если рассматривать вектор X = (x1, x1, xm)T как матрицу размера т 1, то определенные выше нормы будут имеют следующий вид:

1. Первая норма (1-норма)

X 1 xi .

i

2. Вторая норма (Евклидова норма или 2-норма):

3. Бесконечная норма ( -норма):

X max xi .

i

Пример 7

Найти первую, вторую и бесконечную нормы для вектора X (1, 3, 7)T.

X 1 1 3 7 11,

X 2 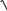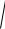12 ( 3)2 ( 7)2 59 7.68,

X max(1, 3, 7) 7.

2.3.Метод простой итерации

Рассмотрим систему линейных уравнений (20) с невырожденной матрицей А. Предположим, что все диагональные элементы матрицы А не равны нулю. Поделим каждую строку системы (20) на соответствующий диагональный элемент матрицы А – aii. Получим систему

14

X* lim X(k)), то предельный вектор X* этого итерационного процесса будет

k

решением системы (24) и, следовательно, исходной системы (21).

Доказательство:

Перейдем в (25) к пределу при k получим:

Для того чтобы запустить итерационный процесс, необходимо задать значения первоначального приближения X(0), тогда все остальные значения X(k) вы-

числяются по формуле (25) . В качестве X(0) обычно берут B.

Решение системы (23) получается в результате бесконечного процесса, и всякий вектор X(k) является приближенным решением.

Метод последовательных приближений, определяемых формулой (25), но-

сит название метода простой итерации.

15

Сформулируем условия, при которых итерационный процесс (25) сходит-

ся.

Теорема 2 (достаточное условие сходимости)

Если в системе (24) ||C|| < 1 (любая норма 1,2,…, ), то процесс (25) сходится к единственному решению при любом начальном приближении X(0).

Условие ||C|| < 1 – равносильно тому, что для матрицы A системы (21) выполняется условие диагонального преобладания по строкам, т.е. элемент, стоящий на диагонали, больше суммы модулей всех остальных элементов своей строки. Это является достаточным условием сходимости метода простой итерации.

Погрешность k-ой итерации можно оценить по формуле:

X* X(k). Т.е. итерации можно прекратить, когда разность между двумя последовательными приближениями станет меньше заданной точности.

Оценка погрешности k-ой итерации, выраженная через разность начальных итераций, задается формулой:

В частности, если в качестве начального приближения взять X(0) = B, то

X(1) B CB, X(1) X(0) B CB B CB.

Тогда X(1) X(0) CBCBCB. Следовательно,

Заметим, что сходящийся процесс итерации обладает важным свойством самоисправляемости, т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, таким образом, ошибочное приближение можно рассматривать как новый начальный вектор.

Пример 8

Привести систему к виду, подходящему для метода простой итерации. Рассчитать аналитически количество итераций для решения системы линейных уравнений методом простой итерации с точностью до 0.001 для каждой переменной. Выполнить три итерации, указать погрешность полученного результата.

16

5x1 3x2 x3 1,2x1 4x2 x3 8,

2x1 2x2 5x3 8.

Разделим первую строку на 5, вторую – на 4, третью – на 5. Преобразованная система

x1 0.6x2 0.2x3 0.2,0.5x1 x2 0.25x3 2,,0.4x1 0.4x2 x3 1.6.

Найдем -нормы матрицы С и вектора B.

C max(0.6 0.2,0.5 0.25,0.4 0.4) max(0.8,0.75,0.8) 0.8.

B max(0.2,2,1.6) 2.

Т.к. C 1, то по теореме 2 итерационный процесс сходится. Количество

шагов метода, необходимых для достижения точности 0.001, найдем, используя формулу (28).

0.8k 1 0.0001, ln(0.8k 1) ln(0.0001), (k 1) ln0.8 ln0.0001,

k 1 ln0.0001 41.2, ln0.8

k 42.

Следовательно, необходимо выполнить 42 шага для достижения точности 0.001 по каждой переменной. Заметим, что эта оценка сильно завышена и на практике следует выполнить гораздо меньшее количество итераций.

Найдем X(1), выполнив один шаг по методу простой итерации при начальном приближении X(0) = B.

Аналогично выполним еще два шага по методу простой итерации:

Оценим погрешность, с которой найдено значение X(3). Для этого найдем

2.4.Метод Зейделя

Метод Зейделя представляет модификацию метода простой итерации. В этом методе при вычислении (k +1)-го приближения переменной xi учитываются уже вычисленные на этом шаге приближения неизвестных x1, x2, xi-1.

Пусть система (20) приведена к виду (24). Выберем начальное приближение X(0). X(k+1) будем вычислять по формулам: