
644_Galkina_M.JU._Vychislitel'naja_matematika_
.pdf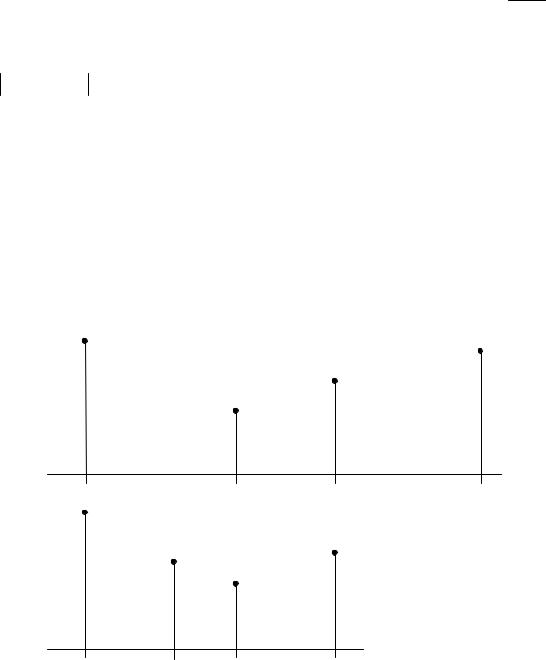
методы поиска, состоящие в вычислениях f (x) в некоторых точках и выбора среди них наибольшего или наименьшего значения. Для успешного применения этих методов обычно необходимо, чтобы функция f (x) была унимодальной, т.е. имела на [a,b] только один минимум или максимум.
Простейшим методом поиска экстремума является метод перебора. Будем для определенности говорить о нахождении минимума. Отрезок, на котором находится минимум, называется интервалом неопределенности. Разобьем от-
резок [a,b] на n равных частей [xi,xi+1] (i = 1, 2, , n) длины h b a . Вычислив n
значение f (x) в узлах xi, найдем среди них наименьшее yk f (xk). Ясно, что минимум находится на отрезке [xk-1,xk+1]. Если выполняется условие, что xk 1 xk 1 , где – заданная точность, то за точку минимума принимаем xk.
Иначе разбиваем отрезок [xk-1,xk+1] на n равных частей и повторяем вычисления. Поскольку вычисление значений f (x) может оказаться весьма трудоемким, то желательно сократить количество таких вычислений. Одним из наиболее
эффективных методов, в котором при ограниченном количестве вычислений достигается наилучшая точность, является метод золотого сечения.
5.2.Метод золотого сечения
Метод состоит в построении последовательности отрезков [a0,b0], [a1,b1],(a0 = a, b0 = b), стягивающихся к точке минимума f (x), причем на каждом шаге вычисление значения f (x) производится только один раз. Рис. 5 иллюстрирует идею метода.
а)
f (x1) f (x2)
a0 |
x1 |
x2 |
b0 |
б)
f (x1)
a1= a0 |
x1 |
x2=x1 |
b1=x2 |
Рис. 5. Метод золотого сечения
На первом шаге внутри отрезка [a0,b0] выбираем две внутренние точки x1 и x2 и вычисляем значения f (x1) и f (x2) (рис. 5, а). Пусть, для определенности, f (x1) < f (x2). Тогда очевидно, что минимум расположен на отрезке [a0,x2], и этот
31

отрезок можно взять в качестве нового интервала неопределенности. Второй шаг метода проводим на отрезке [a1,b1] (a1 = a0, b1 = x2) (рис. 5, б). Теперь опять нужно выбрать две внутренние точки, но одна из них (x1) осталась с предыдущего шага (она становится новой x2 для нового интервала), поэтому достаточно выбрать лишь одну точку x1, вычислить f (x1) и произвести сравнение и т.д. до тех пор, пока не будут достигнута заданная точность.
Рассмотрим способ размещения внутренних точек на каждом отрезке [ak,bk]. Пусть длина интервала неопределенности равна l, а точка деления делит его на части l1, l2: l1 > l2, l1 + l2 = l. Золотое сечение интервала неопределенности выбирается из соотношения:
l1 l2 . l l1
Преобразуем (50) и найдем отношение l2 . l1
l12 l2l,
l12 l2(l1 l2), l12 l1l2 l12 0,
l2 |
2 |
|
l2 |
1 0. |
|
|
|
|
|
||
l |
l |
||||
1 |
|
1 |
|
||
Решив квадратное уравнение, находим |
l2 |
|
1 5 |
. |
|||||||||||
l1 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку |
|
нас интересует только |
положительное |
||||||||||||
|
l2 |
|
l1 |
|
1 |
|
|
|
0.618. Откуда |
|
|
|
|||
|
|
|
5 |
|
|
|
|||||||||
|
l1 |
|
|
|
|
|
|
|
|
||||||
|
|
l |
2 |
|
|
|
l1 0.618l,l2 |
0.382l. |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
(50)
значение, то
(51)
|
Итак, алгоритм метода золотого сечения для поиска |
минимального значе- |
||||||
ния функции можно описать следующим образом: |
|
|
|
|||||
1. |
Находим точки золотого сечения из (51) для интервала неопределенности |
|||||||
|
[a,b]: y 0.618a 0.382b, |
z 0.382a 0.618b. |
|
|
|
|||
2. |
Находим значения функции в точках y и z: A f (y), |
B f (z). |
|
|||||
3. |
Если |
A B, |
то новый |
интервал неопределенности |
[a,z], где |
|||
|
B A, |
z y, |
y 0.618a 0.382b, вычисляем новое |
значение |
A f (y) и |
|||
|
переходим на п.3. Иначе переходим на п.4. |
|
[y,b], |
|
||||
4. |
Новый |
|
интервал |
|
неопределенности |
|
где |
|
|
A B, |
y z, |
z 0.382a 0.618b, вычисляем новое |
значение |
B f (z) и |
|||
|
переходим на п.3. |
|
|
a b |
|
|
||
5. |
Вычисления прекращаются, когда b a . Тогда x |
. |
|
|||||
|
|
|||||||
2
32

5.3.Задание на лабораторную работу №5
Написать программу для нахождения максимального значения функции
f (x) e x (x 1) (x 10) (x N 1) (x 0.5) на отрезке [0; 0.5] методом золотого сечения с точностью 0.0001. Считается, что требуемая точность достигнута, если выполняется условие |bk ak | , ( – заданная точность, ak, bk – гра-
x (x 1) (x 10) (x N 1) (x 0.5) на отрезке [0; 0.5] методом золотого сечения с точностью 0.0001. Считается, что требуемая точность достигнута, если выполняется условие |bk ak | , ( – заданная точность, ak, bk – гра-
|
x |
* |
a b |
||
ницы интервала неопределенности, k = 0,1,2, ), при этом, |
|
|
, |
||
2 |
|||||
fmax f (x*). N – последняя цифра зачетной книжки. |
|
|
|
||
|
|
|
|
||
6. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
6.1.Постановка задачи
Пусть известны значения функции y f (x) в точках х0, х1, …, хn: yi = f (xi).
xn
Необходимо найти значение f (x)dx. Основная идея численного интегриро-
x0
вания заключается в том, чтобы заменить функцию f (x) на интерполирующую
xn xn
ее функцию y(x) (которую можно проинтегрировать), f (x)dx y(x)dx.
x0 x0
Обычно в качестве интерполирующей функции используется интерполяционный многочлен. Заменяя подынтегральную функцию каким-нибудь интерполяционным многочленом, получаем квадратурные формулы вида:
b n
f (x)dx Ai f (xi) R,
a i 0
где Ai – коэффициенты, зависящие только от выбора узлов интерполяции, R – остаточный член или погрешность квадратурной формулы.
При отбрасывании R возникает погрешность усечения.
Квадратурные формулы для равноотстоящих узлов называются формулами Ньютона-Котеса. Формулы Ньютона-Котеса различаются степенями использованных интерполяционных многочленов. Чтобы не иметь дело с многочленами высоких степеней, обычно разбивают промежуток интегрирования на отдельные участки, применяют формулы Ньютона-Котеса с невысокими степенями на каждом участке и потом складывают полученные результаты. Наиболее простыми из формул такого типа являются формулы прямоугольников, трапеций и Симпсона.
33
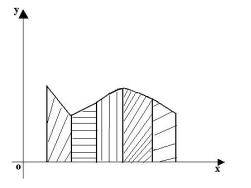
6.2.Формула трапеций
Соединяя каждые два узла прямой (т.е. применяя линейную интерполяцию), получим, что площадь под кривой приближенно равна сумме площадей трапеций (рис. 6). Пусть xi xi 1 const h, i 1,2, n.
x0 x1 xn
Рис. 6. Метод трапеций
b xn |
x1 |
x2 |
|
xn |
|
Тогда |
f (x)dx |
f (x)dx |
f (x)dx ... |
|
f (x)dx |
a x0 |
x0 |
x1 |
|
xn 1 |
|
|
y y |
|
y y |
2 |
|
|
|
y |
n 1 |
y |
n |
|
|
||||
h |
|
0 1 |
|
h |
1 |
|
... h |
|
|
|
|
|
|||||
2 |
2 |
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Получаем формулу трапеций |
|
|
|
|
|
||||||||||
|
|
|
b |
|
|
|
y0 y |
|
|
|
|
|
|
|
|
||
|
|
|
|
f (x)dx h( |
y1 y2 |
||||||||||||
|
|
|
|
||||||||||||||
|
|
|
a |
|
|
|
|
|
2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h( |
y0 y |
y y |
2 |
y |
n |
). |
||||||
|
||||||||||||
|
|
|
2 |
|
1 |
|
|
|
|
|||
|
|
|
|
n |
|
|
|
|
|
|
|
|
y |
n |
), x |
a, x |
b,h |
b a |
|
. (52) |
|||||
|
|
|||||||||||
|
0 |
|
n |
|
|
|
n |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Погрешность усечения составляет
|
|
|
|
|
|
|
(b a)h2 |
|
|
|
|
|
|
|
(53) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Rусеч |
|
|
M2, где M2 max |
f |
. |
||||||||
|
|
|
|
12 |
(x) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
[a,b] |
|
|
|
|
|
||
|
Формула трапеций дает точное значение интеграла, когда подынтегральная |
||||||||||||||||
функция линейна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
По таблице значений функции найти f (x)dx методом трапеций. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
x |
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
|
|
|
|
|
|
|
y |
0 |
|
1 |
|
4 |
|
9 |
|
16 |
|
|
|
|
|
|
|
|
4 |
|
|
0 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
h 1, f (x)dx 1 ( |
1 4 9) 22. |
|
|
|
|
||||||||||||
2 |
|
|
|
|
|||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
34
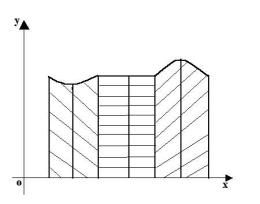
6.3.Формула Симпсона
Соединяя каждые три узла параболой (т.е. применяя квадратичную интерполяцию), получим, что площадь под кривой приближенно равна сумме площадей криволинейных трапеций под параболами (рис. 7). Очевидно, что в этом случае число узлов должно быть нечетным (т.е. n – четное). Пусть
xi xi 1 const h, |
i 1,2, n. |
x0 x1 x2 xn-2 xn-1 xn
Рис. 7. Метод Симпсона
|
|
|
|
xn |
|
|
|
|
|
x2 |
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда |
f (x)dx |
f (x)dx |
|
f (x)dx ... |
|
f (x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
x0 |
|
|
|
|
|
x0 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
xn 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2h |
|
1 |
y |
|
|
2 |
y |
1 |
y |
|
|
2h |
|
1 |
y |
|
|
|
2 |
y |
|
|
1 |
y |
|
... 2h |
|
1 |
y |
|
|
2 |
y |
|
|
1 |
y |
|
|
||||||||
|
|
0 |
|
|
2 |
|
|
|
2 |
|
|
|
4 |
|
n 2 |
|
n 1 |
|
n |
||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
3 |
1 |
6 |
|
|
6 |
|
|
3 |
3 |
|
6 |
|
|
|
|
6 |
|
|
3 |
|
6 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
h |
(y y |
n |
4(y |
1 |
y |
2 |
y |
n 1 |
) 2( y |
|
2 |
y |
4 |
y |
n 2 |
)). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
3 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Получаем формулу Симпсона
b |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
(y0 yn 4(y1 y3 yn 1) 2(y2 y4 yn 2)), |
|||||||||||||||||||
|
|||||||||||||||||||||
a |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где x a, x |
n |
b,h |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Погрешность усечения формулы Симпсона составляет |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
R |
|
(b a)h4 |
M |
4 |
, |
где M |
4 |
max |
|
f (4) |
(x) |
|
. |
||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
усеч |
180 |
|
|
|
[a,b] |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(54)
(55)
Формула Симпсона дает точное значение интеграла, когда подынтегральная функция является многочленом до третьей степени включительно.
Погрешность округления общей формулы трапеции и общей формулы Симпсона одинакова и составляет (b a) , где - погрешность вычисления yi.
Пример 12
В условиях предыдущего примера вычислить интеграл по методу Симпсо-
на.
35

4
h 1, f (x)dx 1 (0 16 4 (1 9) 2 4) 21.333.
3
0
6.4.Метод двойного пересчета
При практических вычислениях часто бывает затруднительно оценить погрешность усечения формулы трапеции или формулы Симпсона из-за того, что
неизвестна f (для формулы трапеций) или f (4) (для формулы Симпсона). В этом случае используется метод двойного пересчета, который заключается в следующем. Вычисляем интеграл Ih по приближенной формуле с шагом h и вычисляем интеграл Ih/2 с шагом h/2 . Если Ih Ih/2 , где – заданная точность, то вычисления заканчивают и считают, что значение интеграла равно Ih/2. В противном случае вычисляют интеграл с шагом h/4 и т.д.
7.ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
7.1.Постановка задачи
Дифференциальными уравнениями первого порядка называются уравнения, содержащие производную первого порядка. Если задано начальное условие, то имеем задачу Коши, которая в общем случае имеет вид:
y'(x) f (x,y), |
(56) |
||||
y(x |
) y |
0 |
. |
||
|
0 |
|
|
|
|
Требуется найти функцию f (x), удовлетворяющую (56). Численное решение такой задачи получают, изменяя x0 на малую величину h и переходя к новой точке x1 = x0 + h. При этом значение функции в точке x1 определяется по наклону кривой в точке x0, вычисленному с помощью дифференциального уравнения. Затем, изменяя x1 на малую величину h и переходя к новой точке x2 = x1 + h, аналогичным образом находят f(x1) и т.д. до тех пор, пока не дойдем до нужной точки. Таким образом, график численного решения задачи Коши – это последовательность отрезков прямых, которыми аппроксимируется кривая y f (x).
7.2.Метод Эйлера
Вметоде Эйлера заменяют точное значение f (x0+h) на значение касательной, проведенной к графику у = f (х) в точке (х0,у0) (рис. 7).
Формула Эйлера имеет вид:
y(xi 1) y(xi) hf (xi,y(xi)) |
(57) |
или |
|
yi 1 yi hf (xi,yi). |
(58) |
В методе Эйлера на одном шаге возникает погрешность C1 h2, которая накапливается в процессе решения и к концу решения составляет C1 h.
36
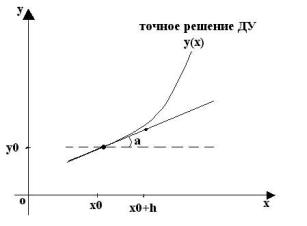
Рис. 8. Иллюстрация метода Эйлера
Пример 13
Найти y(1.3), выполнив 3 шага метода Эйлера для задачи Коши
y y 2x,
y(1) 3.
h |
1.3 1 |
0, |
f (x,y) y 2x. |
||
|
|||||
3 |
|
|
|
|
|
y(x0) y(1) y0 3, |
|
||||
y(x1) y(1.1) y1 y0 |
h f (x0,y0) 3 0.1 f (1,3) 3 0.1 (3 2 1) 3.1, |
||||
y(x2) y(1.2) y2 |
y1 h f (x1,y1) 3.1 0.1 f (1.1,3.1) 3.1 0.1 (3.1 2 1.1) |
||||
3.19, |
|
|
|
||
y(x3) y(1.3) y3 |
y2 |
h f (x2,y2) 3.19 0.1 f (1.2,3.19) |
|||
3.19 0.1 (3.19 2 1.2) 3.269.
7.3.Методы Рунге-Кутта
Лучшие модификации метода Эйлера – методы Рунге–Кутта. Рассмотрим метод Рунге–Кутта с коррекцией в средней точке. Вычисления производятся по формулам:
y* |
|
y |
h |
f (x ,y ), |
|
|
|
2 |
(59) |
||||
i 1/2 |
i |
i |
i |
|||
y |
y hf (x h,y* |
). |
||||
i 1 |
|
i |
|
i |
i 1/2 |
|
Погрешность этого метода равна C3 h2 .
Другой метод Рунге–Кутта – метод с коррекцией по средней производной. Вычисления производятся по формулам:
y* |
y |
hf (x ,y ), |
|
|
|
||||
i 1 |
i |
|
i |
i |
|
|
(60) |
||
y |
y |
|
h |
( f (x ,y ) f (x ,y* |
|||||
|
)). |
||||||||
2 |
|||||||||
i 1 |
i |
i |
i |
i 1 |
i 1 |
|
|||
Погрешность этого метода равна C4 h2 .
На практике чаще всего используют метод Рунге–Кутта четвертого порядка:
37
k1 f (xi,yi), |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
k |
2 |
f (x |
h |
,y |
h |
k ), |
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
i |
2 |
|
i |
2 |
|
1 |
|
|
|
||||||||||
k |
3 |
f (x |
|
h |
,y |
|
h |
k |
2 |
), |
|
(61) |
|||||||||
|
|
|
|
||||||||||||||||||
|
|
i |
2 |
|
|
i |
2 |
|
|
|
|
|
|
||||||||
k4 f (xi h,yi h k3), |
|
|
|||||||||||||||||||
y |
|
y |
h |
(k 2k |
2 |
2k k |
4 |
). |
|||||||||||||
|
|
||||||||||||||||||||
|
i 1 |
i |
6 |
|
|
|
1 |
|
|
|
|
|
|
3 |
|
||||||
Погрешность этого метода равна C5 h4 .
7.4.Метод двойного пересчета
Явные оценки для погрешности решения весьма затруднительны, т.к. константы, участвующие в оценке погрешности, весьма трудно оценить. Поэтому в практических задачах для достижения заданной точности решения ε используют двойной пересчет. Находят решение дифференциального уравнения на [a,b] дважды: с шагом h и с шагом h/2. Затем сравнивают полученные двумя способами значения функции во всех точках xi, в которых были вычислены оба значения. Считается, что необходимая точность достигнута, если разность этих значений не превосходит ε для методов первого порядка точности, 3ε для методов второго порядка, 15ε для методов четвертого порядка.
8. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Напряжение в электрической цепи описывается дифференциальным уравнением с начальным условием:
y cos 2x y 7 x y ,
y 0 0.
|
|
|
|
|
y |
|
|
|
y 1 sin 3x y |
|
, |
||||
1. |
2 x |
||||||
|
1. |
|
|
||||
|
|
|
|
|
|||
|
y 0 |
|
|
|
|||
|
|
|
cosy |
|
|
|
|
|
y |
|
|
y, |
|
|
|
2. |
|
4 x |
|
|
|||
|
|
|
|
|
|||
|
|
0.1. |
|
|
|||
|
y 0 |
|
|
||||
y 1 5 x sinx 3 x y,
y 0 0.
y 6 y2 cosx 2y,
y 0 0.3.
5.y 1 3y sinx y,
y 0 0.2.
38
6.y 1 3y sinx y,
y 0 0.4.
7.y cos(4x y) 3(x y),
y 0 0.
|
|
|
y |
|
|
|
y sin(5x y) |
|
, |
||
8. |
2 3x |
||||
|
0.2. |
|
|||
|
|
|
|
||
|
y 0 |
|
|
||
9.y 6sinx (3 x)y,y 0 0.1.
Написать программу, которая определит количество теплоты, выделяющееся на единичном сопротивлении за единицу времени. Количество теплоты
1
определяется по формуле: Q y2dt. Дифференциальное уравнение решить
0
методом Рунге–Кутта четвертого порядка с точностью 10-4. Интеграл вычислить по формуле Симпсона с шагом 0.1. Для нахождения значений функции в промежуточных узлах применить линейную интерполяцию. Вывести решение дифференциального уравнения, результаты интерполяции и количество теплоты.
Номер уравнения выбирается по последней цифре зачетной книжки.
Методические указания к выполнению курсовой работы
Для достижения заданной точности при решении дифференциального уравнения использовать метод двойного пересчета. Начальный шаг решения равен половине интервала, на котором решается уравнение, т.е. 0.5.
39
ЛИТЕРАТУРА
1.Волков Е. А. Численные методы. М.: Наука, 1987. 248 с.
2.Демидович Б. П., Марон И. А. Основы вычислительной математики. М.:
Наука, 1970. 664 с.
3.Турчак Л. И. Основы численных методов. М.: Наука, 1987. 286 с.
4.Азаров А. И., Басик В. А., Мелешко И. Н. и др. Сборник задач по методам вычислений. М.: Наука, 1994. 319 с.
5.Амосов А. А., Дубинская Ю. А., Копченов Н. В. Вычислительные методы для инженеров. М.: Высшая школа, 1994. 544 с.
6.Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. М.: Лаборатория базовых знаний, 2000. 640 с.
7.Данилина Н. И., Дубровская Н. С., Кваша О. П., Смирнов Г. Л. Вычислительная математика. М.: Высшая школа, 1985. 472 с.
8.Лапчик М. П., Рагулина М. И., Хеннер Е. К. Численные методы. М.: Акаде-
мия, 2005. 384 с.
40
