1.4 Уравнения прямой и плоскости в пространстве

Справедливо следующее утверждение: если в пространстве дана произвольная декартова прямоугольная система координат , то всякое линейное уравнение с тремя переменными и определяет относительно этой системы плоскость, уравнение которой имеет вид:

, (23)

где не равны нулю одновременно.

Уравнение (23) называется общим уравнением плоскости, причём числа

являются координатами некоторого вектора , который нормален к плоскости.

Уравнение

(24)

эквивалентно уравнению (23) и определяет плоскость, проходящую через заданную точку и перпендикулярную вектору . Вектор мы будем называть нормальным вектором плоскости.

Уравнение плоскости в отрезках на осях таково:

, (25)

где отрезки, отсекаемые плоскостью соответственно на осях .

Уравнение плоскости, проходящей через точку , параллельно двум неколлинеарным векторам и , записывается так:

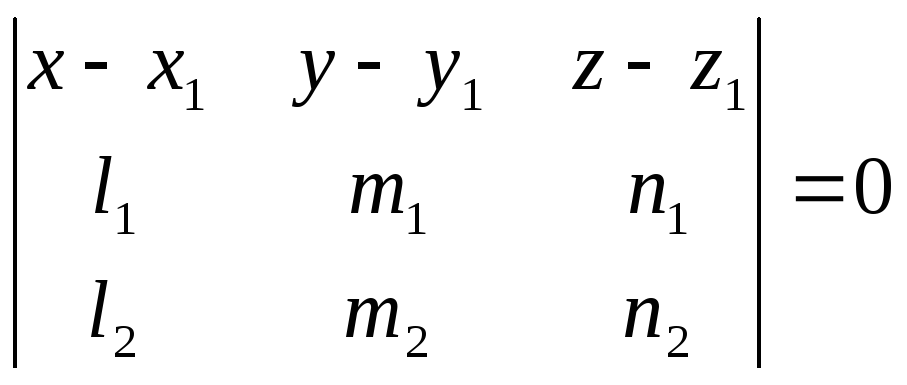. (26)

Уравнение плоскости, проходящей через точки и , параллельно вектору , неколлинеарному вектору пишется в виде:

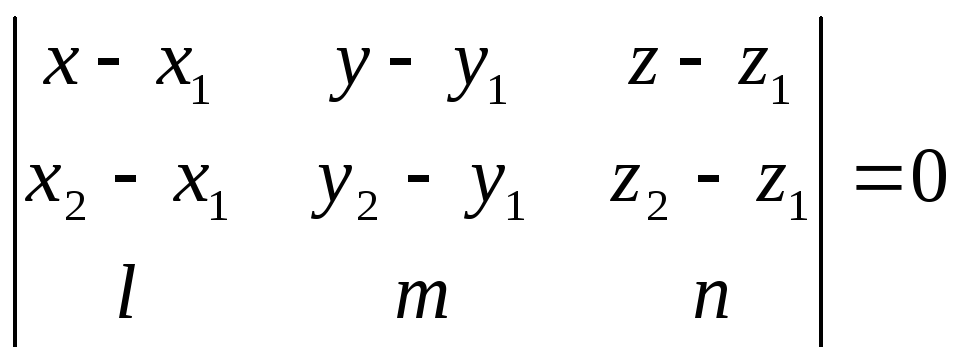. (27)

Уравнение плоскости, проходящей через 3 точки, не лежащие на одной прямой, записывается так:

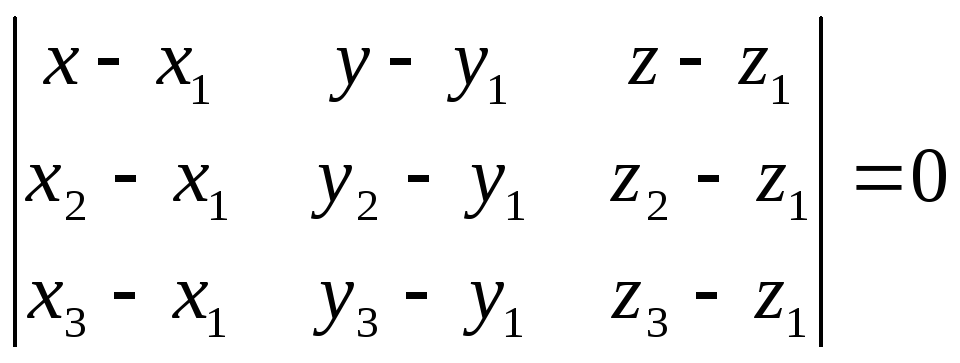. (28)

Угол между плоскостями и с векторами нормалей и определяется по формуле:

. (29)

Необходимым и достаточным условием совпадения двух плоскостей является пропорциональность всех коэффициентов их общих уравнений, т.е.

. (30)

Необходимым и достаточным условием параллельности двух плоскостей является пропорциональность коэффициентов при :

причём . (31)

Необходимым и достаточным условием того, что три плоскости

имеют одну общую точку, является условие

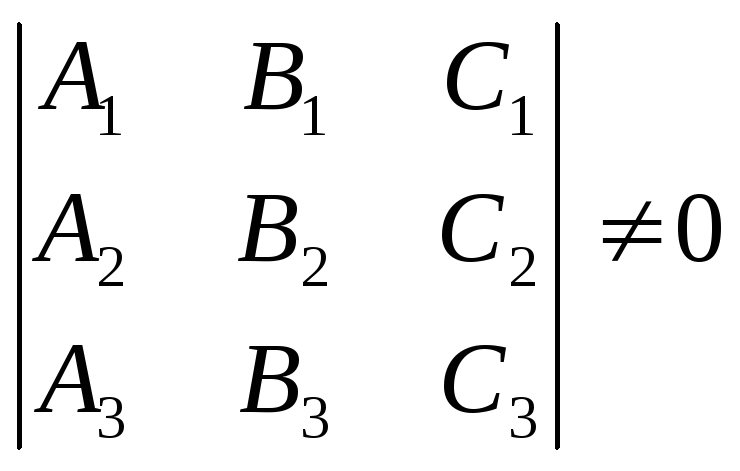. (32)

Необходимым и достаточным условием перпендикулярности двух плоскостей является условие , т.е.

. (33)

Расстояние от точки до плоскости в прямоугольной системе координат находится по формуле:

. (34)

Если плоскость не проходит через начало координат и углы вектора нормали , имеющего начало в начале координат с осями , то нормальное уравнение плоскости имеет вид:

. (35)

Чтобы общее уравнение (23) плоскости привести к нормальному виду (35), нужно общее уравнение плоскости умножить на . Знак перед дробью выбирается противоположным знаку .

Прямая в пространстве - линия пересечения 2-х непараллельных плоскостей, если плоскости заданы общими уравнениями, то прямая в общем виде задаётся, как результат пересечения этих плоскостей, то есть системой уравнений

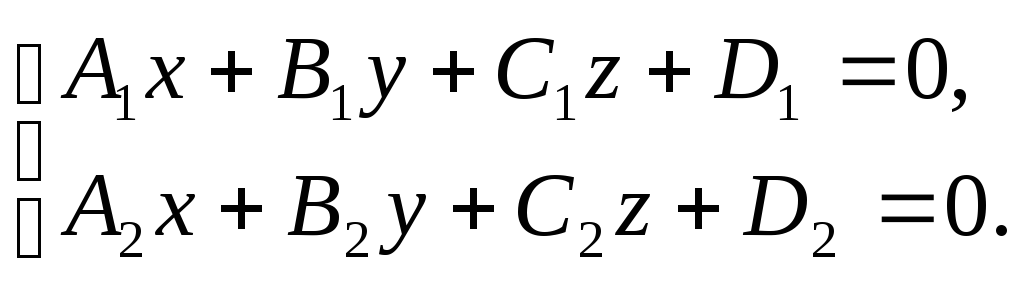(36)

Прямая, проходящая через точку , параллельно вектору (направляющий вектор прямой), определяется уравнениями:

, (37)

или

, (38)

где (37) – параметрические уравнения прямой, (38) – канонические уравнения.

Если прямая задана двумя точками и , то канонические уравнения прямой запишутся в виде:

. (39)

Необходимое и достаточное условие того, что две прямые

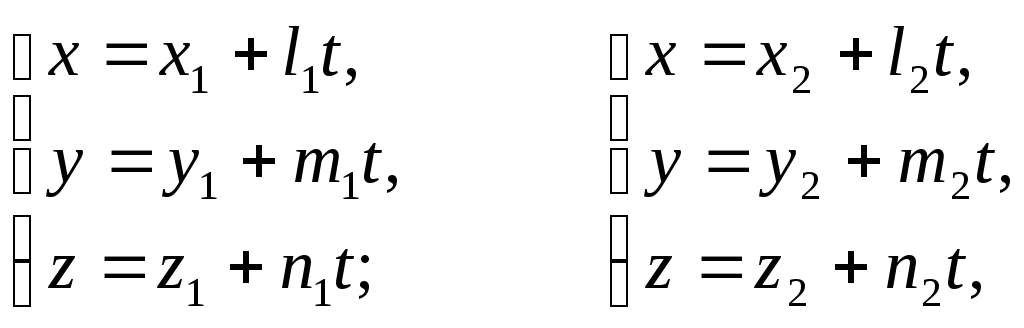
лежат в одной плоскости, записывается в виде:

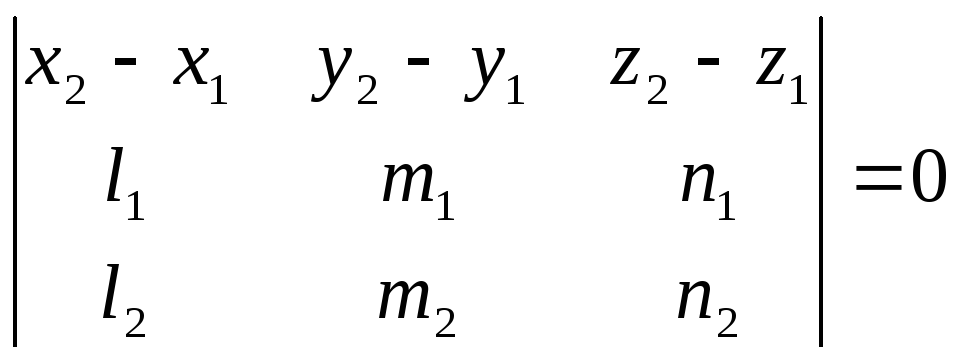. (40)

Условие параллельности двух прямых имеет вид:

. (41)

Условие перпендикулярности двух прямых:

. (42)

Углы между двумя прямыми в прямоугольной системе координат определяются соотношениями:

. (43)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Составить уравнение плоскости, проходящей через три точки .

Решение. Воспользуемся уравнением плоскости (28), проходящей через три точки:

=.

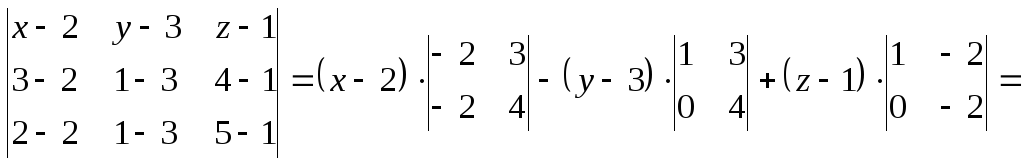
Раскрыв определитель по элементам первой строки, получаем уравнение плоскости:

или

.

Задача 2. Определить объём тетраэдра, ограниченного координатными плоскостями и плоскостью .

Решение. Пусть объём тетраэдра. , где площадь основания, высота.

В основании тетраэдра лежит прямоугольный треугольник, катеты которого есть отрезки, отсекаемые плоскостью на осях и . Высота тетраэдра, опущенная на основание, есть отрезок, отсекаемый плоскостью на оси . Поэтому, чтобы найти объём тетраэдра, нужно записать уравнение плоскости в виде , где отрезки, отсекаемые этой плоскостью на осях соответственно.

Разделив обе части на 18, получим . Итак, .

(ед³).

Задача 3. Составить уравнение плоскости, проходящей через две точки и и параллельной вектору .

Решение. Векторы и неколлинеарны, так как их координаты не пропорциональны.

.

.

Следовательно, можно воспользоваться уравнением (27). Подставив вместо и координаты точек и вектора соответственно, получим:

.

Таким образом, получили уравнение:

.

Разделим обе части полученного уравнения на и приведём подобные, окончательно получаем:

.

Задача 4. Даны две точки . Составить уравнение плоскости, проходящей через точку и перпендикулярной к прямой .

Решение. Уравнение плоскости будем искать по формуле (24).

Вектор перпендикулярен искомой плоскости, так как прямая перпендикулярна плоскости.

.

Следовательно, . Вместо подставим координаты точки .

,

.

уравнение искомой плоскости.

Задача 5. Определить расстояние от точки до плоскости .

Решение. Запишем уравнение плоскости в нормальном виде. Выпишем нормирующий множитель . В нашем случае . Следовательно, .

Так как свободный член в уравнении плоскости положительный, то обе части уравнения умножим на :

.

Пусть расстояние от точки до плоскости . Тогда

.

Задача 6. Составить уравнение прямой, проходящей через точки , .

Решение. В уравнения (38) подставим вместо и координаты точек и соответственно:

.

Канонические уравнения искомой прямой:

.

Задача 7. Составить параметрические уравнения прямой

Решение. Прямая задана как результат пересечения двух плоскостей. Чтобы записать параметрические уравнения прямой, нужно знать координаты какой-нибудь точки, принадлежащей прямой, и вектор, параллельный прямой, то есть её направляющий вектор.

Точку, принадлежащую прямой, можно найти, если решить систему уравнений, задающих прямую. Так как уравнений два, а неизвестных три, то одно неизвестное, например , нужно определить произвольным образом, положив его равным какому-либо числу. Но в данной задаче обе плоскости проходят через начало координат, то есть через точку , так как их свободные члены равны нулю. Следовательно, в качестве точки, принадлежащей прямой, можно взять точку .

В качестве направляющего вектора прямой возьмём вектор , где и нормальные векторы плоскостей. Здесь мы воспользовались тем фактом, что результат векторного произведения двух ненулевых векторов перпендикулярен плоскости этих векторов. То есть и , следовательно, вектор параллелен прямой.

.

Искомые уравнения прямой:

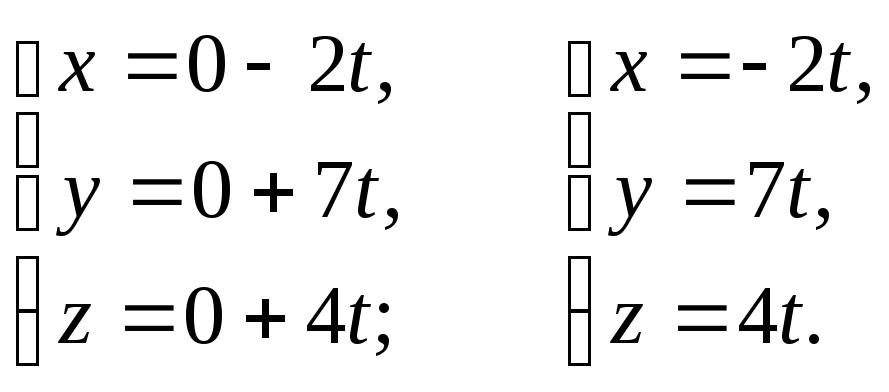
Задача 8. Установить, лежат ли следующие точки на одной прямой: , , .

Решение. Напишем канонические уравнения прямой, проходящей, например, через точки и :

,

.

Если три точки лежат на одной прямой, то координаты третьей точки должны удовлетворять полученным уравнениям прямой. Вместо подставим соответственно:

.

Следовательно, все три заданные точки лежат на одной прямой.

Задача 9. Найти точку пересечения прямой с плоскостью .

Решение. Подставим вместо в уравнение плоскости: соответственно:

.

Отсюда . Найденное значение параметра , соответствующее общей точке прямой и плоскости, подставим в параметрические уравнения прямой:

.

координаты точки пересечения.

Задача 10. Составить уравнение плоскости, проходящей через точку и через прямую .

Решение. Решение данной задачи сводится к написанию уравнения плоскости, проходящей через две заданные точки, параллельно некоторому вектору.

Так как прямая принадлежит плоскости, то точка , через которую проходит эта прямая, также принадлежит плоскости. Направляющий вектор прямой параллелен плоскости.

Подставляя координаты точек и вектора в уравнение (27), получим:

;

;

.

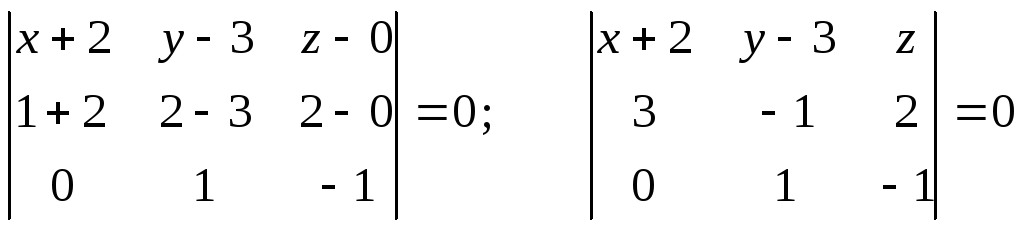Уравнение плоскости: .