
1.1.2 Свойства определителей
10. При перемене местами двух строк (или столбцов) определителя его знак меняется на противоположный, а абсолютная величина не меняется.
20. Определитель с двумя одинаковыми строками или столбцами равен нулю.
30. Умножение всех элементов некоторой строки (или столбца) определителя на число λ, равносильно умножению определителя на это число, т.е. постоянный множитель можно выносить за знак определителя из любой строки или любого столбца.
40. Если все элементы некоторой строки (или столбца) равны нулю, то определитель равен нулю.
50. Если элементы двух строк (или столбцов) определителя пропорциональны, то определитель равен нулю.
60. Если к элементам некоторой строки (или столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на действительное число λ, то величина определителя не изменится.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Найти
определитель матрицы
![]() .
.
Решение.
![]() .
.
Пример 2. Вычислить
определитель:
![]() .
.
Решение.
![]() .
.
Пример 3. Решить
уравнение:
![]() .
.
Решение. Вычислим определитель:
![]() ;
;
![]() ;
;
![]() или
или
![]() ;
;
![]() или
или
![]() .
.
Ответ. -4; -1.
Пример 4. Решить
уравнение:
![]() .
.
Решение. Вычислим определитель:
![]() .
.
При решении воспользовались формулой:
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
Ответ.
![]() .
.
Пример 5. Вычислить
определитель 3-го порядка
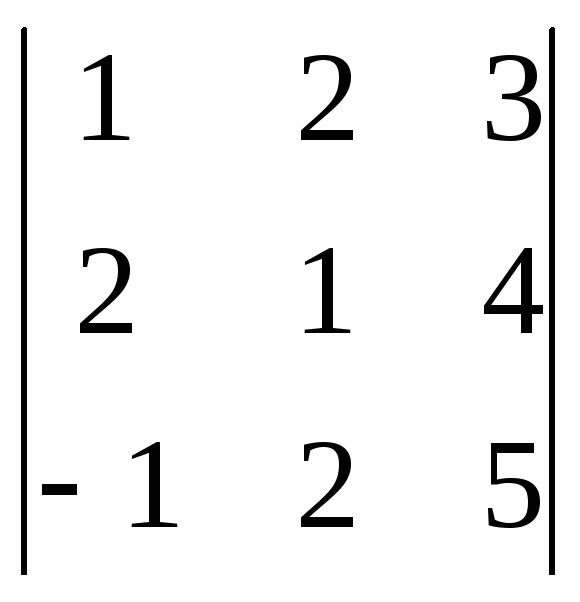 .
.
Решение. Вычислим данный определитель по правилу (2).
 .
.
Пример 6. Вычислить
определитель
![]()
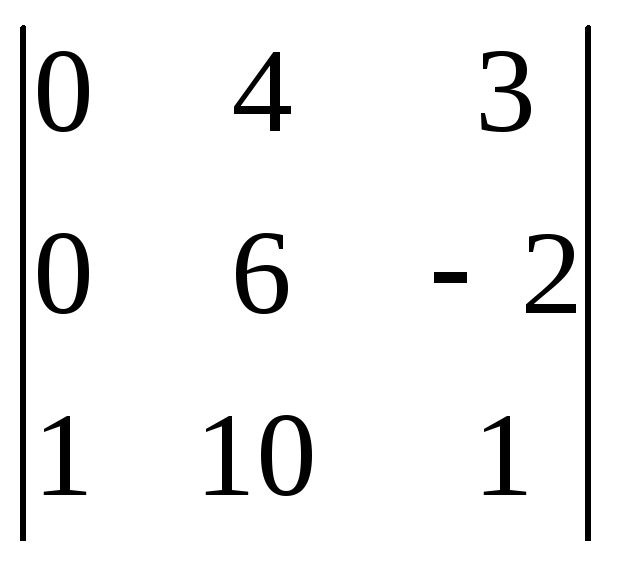 .
.
Решение. Данный определитель можно вычислить и по правилу (2), но так как первый столбец определителя содержит два нуля, то целесообразней разложить данный определитель по элементам первого столбца:
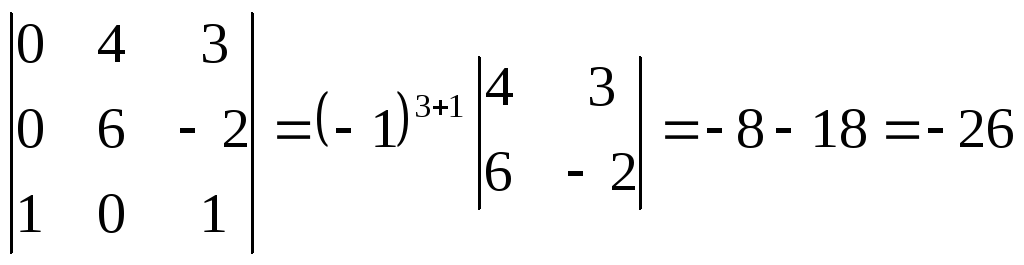 .
.
Пример 7. Вычислить
определитель
 .
.
Решение. В данном определителе нет нулевых элементов, поэтому вычислим его по правилу (2).
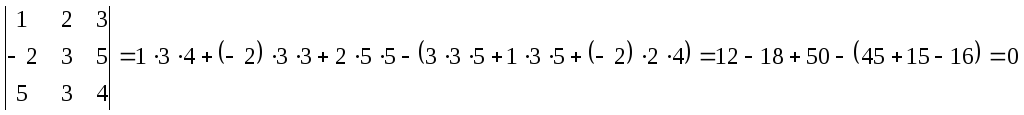 .
.
Пример 8. Решить
неравенство:
 .
.
Решение. Вычислим сначала определитель, используя правило (2).
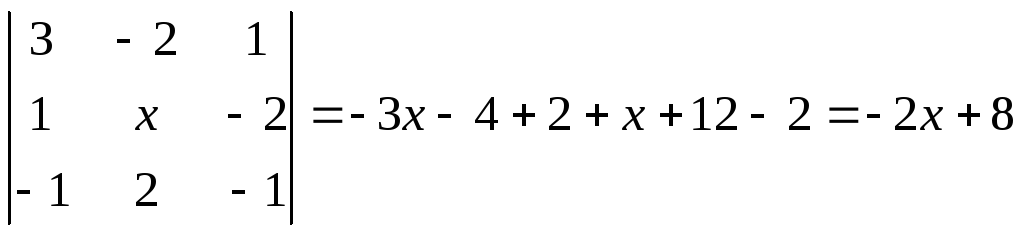 .
.
Далее решаем неравенство
![]() ;
;
![]() ;
;
![]() .
.
Ответ.
![]() .
.
Пример 9. Вычислить
определитель 4-го порядка, используя
разложение по элементам первой строки:
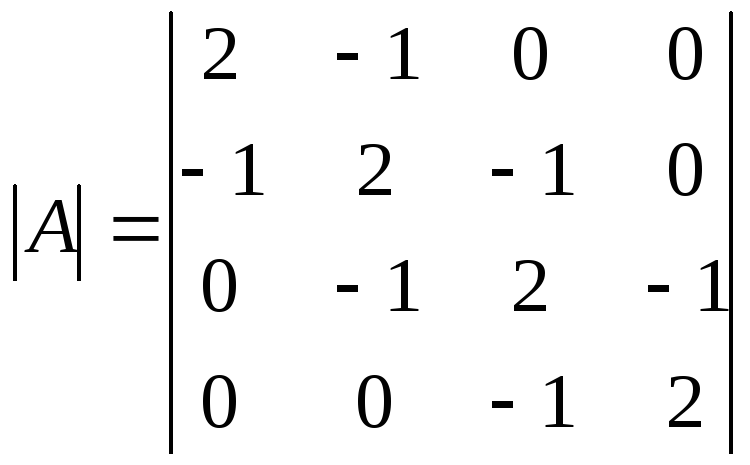 .
.
Решение. Используя формулу (3), разложим данный определитель по первой строке:
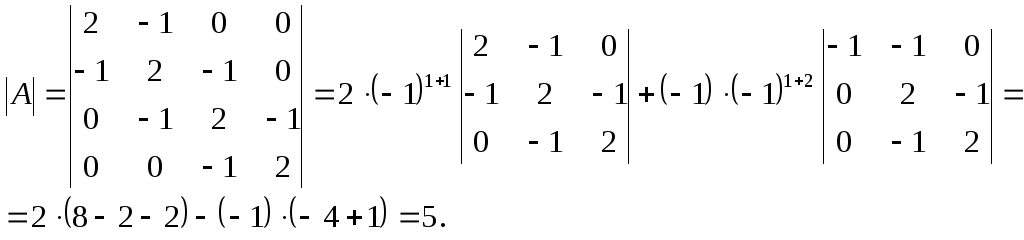
Здесь определители
третьего порядка представляют собой
миноры
![]() элементов
элементов
![]() .
Эти определители можно вычислить либо
по формуле (2), как это сделано выше, либо
по правилам (3), (4).
.
Эти определители можно вычислить либо
по формуле (2), как это сделано выше, либо
по правилам (3), (4).
1.2 Элементы векторной алгебры
Пусть на плоскости дана декартова прямоугольная система координат.
Из школьного курса
геометрии известно, что каждая точка
![]() плоскости в данной системе координат
однозначно характеризуется двумя
числами
плоскости в данной системе координат
однозначно характеризуется двумя
числами
![]() ,
которые называются координатами
точки
,
которые называются координатами
точки
![]() .
Эти же два числа называются координатами
вектора
(геометрического)
.
Эти же два числа называются координатами
вектора
(геометрического)
![]() ,
начало которого (точка O)
совпадает с началом координат, а конец
находится в точке
,
начало которого (точка O)
совпадает с началом координат, а конец
находится в точке
![]() .
.
Аналогично, каждой
точке
![]() трёхмерного пространства в заданной
прямоугольной декартовой системе
координат соответствует упорядоченная
тройка чисел
трёхмерного пространства в заданной
прямоугольной декартовой системе
координат соответствует упорядоченная
тройка чисел
![]() ,
называемых координатами точки
,
называемых координатами точки
![]() .
Эти же три числа называются координатами
геометрического вектора
.
Эти же три числа называются координатами
геометрического вектора
![]() в прямоугольной декартовой системе
координат в трёхмерном пространстве.
в прямоугольной декартовой системе
координат в трёхмерном пространстве.
В геометрии вектором
(геометрическим)
![]() называют направленный отрезок прямой;
при этом отрезок прямой линии называется
направленным отрезком, если указано,
какой из его концов считается началом
отрезка, а какой – концом.
называют направленный отрезок прямой;
при этом отрезок прямой линии называется
направленным отрезком, если указано,
какой из его концов считается началом
отрезка, а какой – концом.
В аналитической геометрии рассматривают пространство «свободных» векторов, т.е. отождествляют (считают равными) любые два вектора, которые совпадают, если при параллельном переносе совместить их начала. Поэтому мы можем всё пространство таких «свободных» векторов отождествить с пространством векторов, исходящих из начала координат.
Определение 4.
Длиной вектора
![]() называют число
называют число
![]() ,
равное
,
равное
![]() .
(5)
.
(5)
Определение 5. Вектор называется нулевым, если начало и конец его совпадают, т.е. его длина равна 0.
Определение 6. Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.
Определение 7. Два
вектора
![]() и
и
![]() называются равными
называются равными
![]() ,
если они коллинеарны, имеют одинаковую
длину и сонаправлены, т.е. если
,
если они коллинеарны, имеют одинаковую
длину и сонаправлены, т.е. если
![]() для всех значений индекса
для всех значений индекса
![]() .
.
Определение 8. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Линейные операции над векторами
Линейными операциями над векторами принято называть операцию сложения векторов и операцию умножения векторов на вещественные числа.
Сумма векторов
![]() и
и
![]() определяется равенством
определяется равенством
![]() .
.
Произведение
вектора
![]() на действительное число λ определяется
равенством
на действительное число λ определяется
равенством
![]() .
.
Определение 9.
Векторы
![]() называются линейно
независимыми,
если равенство нулю их линейной комбинации
называются линейно
независимыми,
если равенство нулю их линейной комбинации
![]() возможно лишь в случае, когда все числа
возможно лишь в случае, когда все числа
![]() равны нулю.
равны нулю.
Определение 10. Три
линейно независимых вектора
![]() образуют в пространстве базис,
если любой вектор
образуют в пространстве базис,
если любой вектор
![]() этого пространства может быть представлен
в виде некоторой линейной комбинации
векторов
этого пространства может быть представлен
в виде некоторой линейной комбинации
векторов
![]() ,
т.е. существует (и притом единственный)
набор чисел
,
т.е. существует (и притом единственный)
набор чисел
![]() такой, что
такой, что
![]() .
.
При этом числа
![]() называют координатами вектора
называют координатами вектора
![]() в базисе
в базисе
![]() .
.
В случае декартовой
прямоугольной системы координат базисные
векторы принято обозначать буквами
![]() .
Каждый из этих векторов имеет длину,
равную единице и любые два из них
перпендикулярны. Направления векторов
.
Каждый из этих векторов имеет длину,
равную единице и любые два из них
перпендикулярны. Направления векторов
![]() совпадают с направлениями декартовых
осей
совпадают с направлениями декартовых
осей
![]() соответственно.
соответственно.
Выражение
![]()
![]()
означает, что
имеется вектор
![]() ,
координаты которого в прямоугольном
базисе
,
координаты которого в прямоугольном
базисе
![]() равны
равны
![]() .
.
Скалярное произведение векторов
Определение 11.
Скалярным
произведением
двух ненулевых векторов
![]() и
и
![]() называют число
называют число
![]() .
.
Если хотя бы один из них равен нулевому вектору, то их скалярное произведение считается равным нулю.
Угол между векторами
![]() –
наименьший угол между ними.
–
наименьший угол между ними.
Для скалярного
произведения наряду с обозначением
![]() используется также
используется также
![]() .
.
Геометрические свойства скалярного произведения:
1)
![]() (условие перпендикулярности векторов);
(условие перпендикулярности векторов);
2) если
![]() ,
то
,
то
![]() и
и
![]() .
.
Алгебраические свойства скалярного произведения:
1)
![]() (коммутативность);
(коммутативность);
2)
![]() (ассоциативность);
(ассоциативность);
3)
![]() (дистрибутивность).
(дистрибутивность).
Если векторы
![]() и
и
![]() представлены своими координатами в
прямоугольном базисе, то скалярное
произведение равно:
представлены своими координатами в
прямоугольном базисе, то скалярное
произведение равно:
![]() .
(6)
.
(6)
Отсюда, в частности, следует формула для определения косинуса угла между векторами:
![]() .
(7)
.
(7)
Векторное произведение векторов
Определение 12.
Упорядоченная тройка некомпланарных
векторов
![]() называется правой
(левой), если
выполнено одно из следующих трёх условий:
называется правой
(левой), если
выполнено одно из следующих трёх условий:
1) если, будучи приведены к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки;
2) если после
приведения к общему началу вектор
![]() располагается по ту сторону плоскости
векторов
располагается по ту сторону плоскости
векторов
![]() и
и
![]() ,
откуда кратчайший поворот от
,
откуда кратчайший поворот от
![]() к
к
![]() кажется совершающимся против часовой
стрелки (по часовой стрелке).
кажется совершающимся против часовой
стрелки (по часовой стрелке).
3) если, находясь
внутри телесного угла, образованного
приведёнными к общему началу векторами
![]() ,
мы видим поворот от
,
мы видим поворот от
![]() к
к
![]() и от него к
и от него к
![]() ,
совершающимся против часовой стрелки
(по часовой стрелке).
,
совершающимся против часовой стрелки
(по часовой стрелке).
По договорённости
обычно рассматривают только правые
системы координат. Например, тройка
базисных векторов прямоугольной
декартовой системы координат в
![]() является правой.
является правой.
Определение 13.
Векторным
произведением
вектора
![]() на вектор
на вектор
![]() называется вектор, обозначаемый символом
называется вектор, обозначаемый символом
![]() (или
(или
![]() ),
определяемый следующими тремя условиями:
),
определяемый следующими тремя условиями:
1) длина вектора
![]() равна площади параллелограмма,
построенного на векторах
равна площади параллелограмма,
построенного на векторах
![]() и
и
![]() ,
т.е.
,
т.е.
![]() ;
;
2) вектор
![]() перпендикулярен плоскости векторов
перпендикулярен плоскости векторов
![]() и
и
![]() ;
;
3) вектор
![]() направлен так, что упорядоченная тройка
направлен так, что упорядоченная тройка
![]() правая.
правая.
Из определения
следует, что если хотя один из них равен
0 или они коллинеарны, то
![]() .
.
Алгебраические свойства векторного произведения:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Если
![]() и
и
![]() - векторы, заданные своими координатами
в базисе
- векторы, заданные своими координатами
в базисе
![]() ,
то разложение векторного произведения
,
то разложение векторного произведения
![]() в том же базисе имеет вид:
в том же базисе имеет вид:
![]() ,
,
или в символической записи
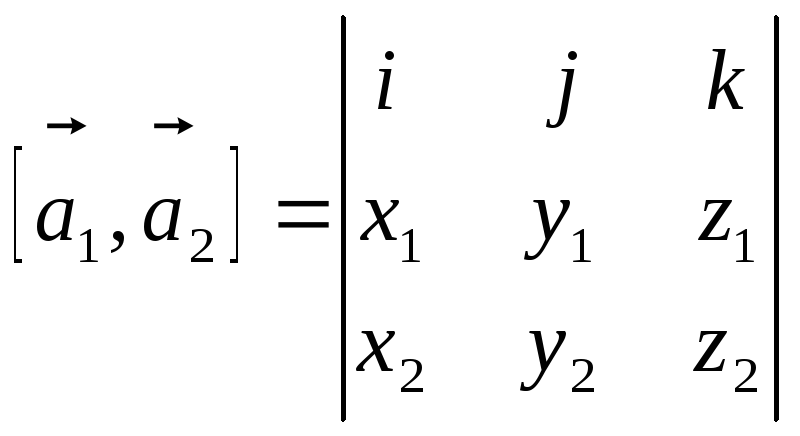 .
(8)
.
(8)
Данный определитель нужно раскладывать по элементам первой строки.
Смешанное произведение векторов
Определение 14.
Смешанным
произведением
упорядоченной тройки векторов
![]() называется число
называется число
![]() ,
которое обозначается
,
которое обозначается
![]() .
.
Геометрические свойства смешанного произведения:
1) если
![]() объём
параллелепипеда, построенного на
векторах
объём
параллелепипеда, построенного на
векторах
![]() ,
то
,
то

2) для того, чтобы
три вектора
![]() были компланарны, необходимо и достаточно
выполнение условия
были компланарны, необходимо и достаточно
выполнение условия
![]() .
.
Смешанное произведение через координаты векторов в прямоугольном базисе записывается в виде:
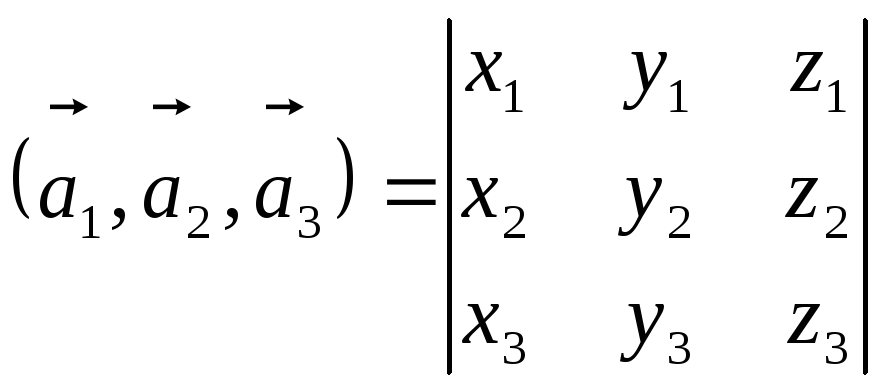 .
(9)
.
(9)
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Известно,
что:
![]() .
.
Вычислить: а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
Решение.
а) По определению скалярного произведения двух векторов:
![]() ,
т.е.
,
т.е.
![]() .
Таким образом, получили, что скалярное
произведение вектора на себя равно
квадрату его длины:
.
Таким образом, получили, что скалярное
произведение вектора на себя равно
квадрату его длины:
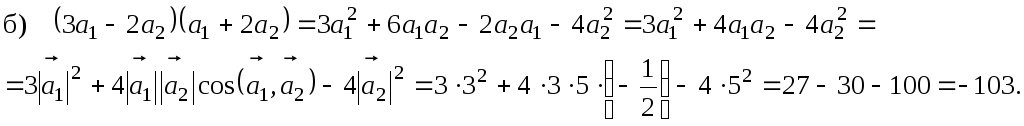

При решении б) и в) пользовались алгебраическими свойствами и определением скалярного произведения.
Задача 2. Даны
векторы
![]() и
и
![]() .
Вычислить: а)
.
Вычислить: а)
![]() ;
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Решение.
а) Воспользуемся формулой (6).
![]() ;
;
б) Вычислим сначала
координаты векторов
![]() и
и
![]() .
.
![]() ;
;
![]() ;
;
Воспользуемся формулой (6):
![]() ;
;
в) Найдём сначала
координаты вектора
![]() .
.
![]() ;
;
![]() ;
;
г) Найдём координаты
вектора
![]() .
.
![]() ;
;
По формуле (5) находим:
![]() .
.
Ответ. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задача 3. При каком
значении
![]() векторы
векторы
![]() и
и
![]() перпендикулярны?
перпендикулярны?
Решение. Т.к.
![]() ,
то имеем:
,
то имеем:
![]() .
.
Решаем квадратное
уравнение относительно
![]() :
:
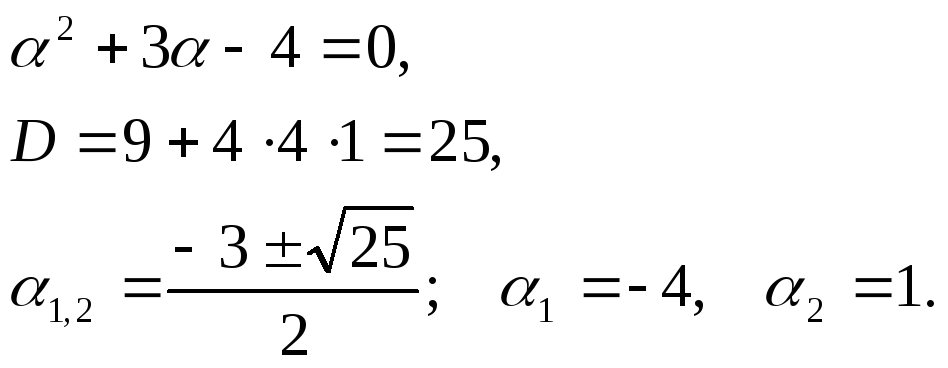
Таким образом, мы
получили два значения
![]() ,
при которых векторы
,
при которых векторы
![]() и
и
![]() будут перпендикулярны.
будут перпендикулярны.
Задача 4. Найти
угол между векторами
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() -единичные
взаимно перпендикулярные векторы.
-единичные
взаимно перпендикулярные векторы.
Решение.
По формуле (7) для определения косинуса
угла между двумя векторами будем иметь
![]() .
.
Найдём сначала
![]() :
:
![]()
Вычислим теперь
длины векторов
![]() и
и
![]() :
:
![]()
![]()
![]() .
.
![]() .
.
Ответ.
![]() .
.
Задача 5. Известно,
что
![]() .
.
Вычислить: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение.
а) Воспользуемся определением векторного произведения:
![]() ;
;
б)
![]() .
.
С учётом 1-го и 2-го свойства векторного произведения получаем:
![]() .
.
![]() ;
;
в)
![]()
По определению векторного произведения находим:
![]() ;
;
Ответ. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Задача 6. Заданы
векторы
![]() и
и
![]() .
Найти координаты векторов: а)
.
Найти координаты векторов: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение.
а) Т.к. векторы
![]() и
и
![]() заданы своими координатами в прямоугольном
базисе, то по формуле (8) находим:
заданы своими координатами в прямоугольном
базисе, то по формуле (8) находим:

Мы получили
разложение вектора векторного произведения
в прямоугольном базисе или
![]() .
.
б) Вычислим
координаты вектора
![]() :
:
![]() .
.
По формуле (8) находим:
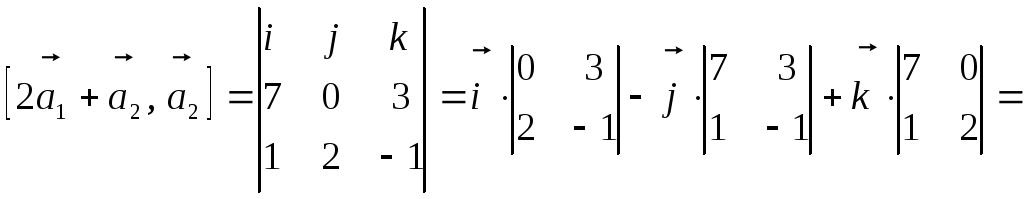
=![]() .
.
![]() .
.
Можно было найти
координаты вектора
![]() другим способом. Если учесть результат,
полученный в п. а), то имеем
другим способом. Если учесть результат,
полученный в п. а), то имеем
![]() .
.
в) Вычислим
координаты векторов
![]() и
и
![]() :
:
![]() .
.
![]() .
.
По формуле (8) находим:
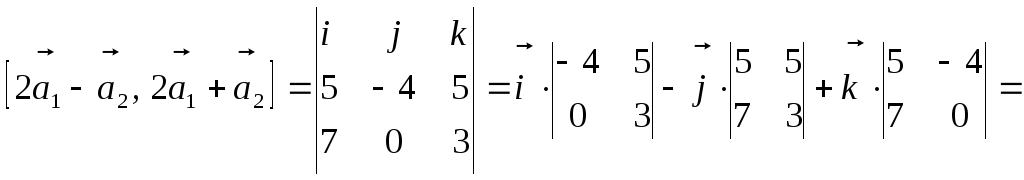
=![]() .
.
![]() .
.
Или, если учитывать результат пункта а):
![]() .
.
Ответ. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
Задача 7. Вычислить
площадь параллелограмма, построенного
на векторах
![]() ,
,
![]() .
.
Решение.
Так как площадь параллелограмма,
построенного на векторах
![]() и
и
![]() ,
равна длине их векторного произведения,
то найдём
,
равна длине их векторного произведения,
то найдём
![]() ,
а затем вычислим длину полученного
вектора.
,
а затем вычислим длину полученного
вектора.
 .
.
![]() (ед2),
(ед2),
где
![]() площадь
параллелограмма.
площадь
параллелограмма.
Задача 8. Вычислить
площадь треугольника с вершинами
![]() ,
,
![]() и
и
![]() .
.
Решение. Площадь треугольника находится по формуле:
![]() .
.
Поэтому найдём
![]() ,
а затем вычислим длину полученного
вектора.
,
а затем вычислим длину полученного
вектора.
![]() ;
;
![]() ;
;
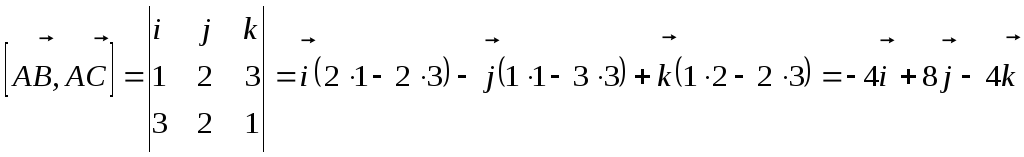 .
.
![]() ,
,
![]() (ед2).
(ед2).
Ответ.
![]() (ед2).
(ед2).
Задача 9. Найти
объём тетраэдра, построенного на векторах
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Отметим, что объём тетраэдра, построенного
на трёх заданных векторах
![]() равен 1/6 объёма параллелепипеда,
построенного на этих же векторах. Объём
параллелепипеда равен абсолютной
величине смешанного произведения
равен 1/6 объёма параллелепипеда,
построенного на этих же векторах. Объём
параллелепипеда равен абсолютной
величине смешанного произведения
![]() .
.
 ,
,
откуда
![]() (ед3).
(ед3).
Задача 10. В тетраэдре
с вершинами в точках
![]() ,
,
![]() ,
,
![]() ,
,
![]() вычислить высоту
вычислить высоту
![]() .
.
Решение. Из курса геометрии известно, что объём тетраэдра находится по формуле:
![]() .
.
Объём тетраэдра
равен
![]() .
Найдём координаты векторов
.
Найдём координаты векторов
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
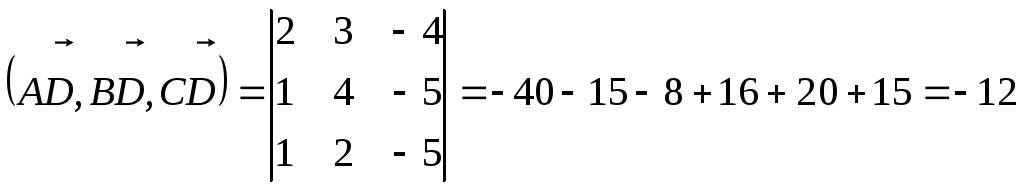 ,
,
откуда
![]() (ед3).
(ед3).
![]() .
.
![]() ;
;
![]() ;
;
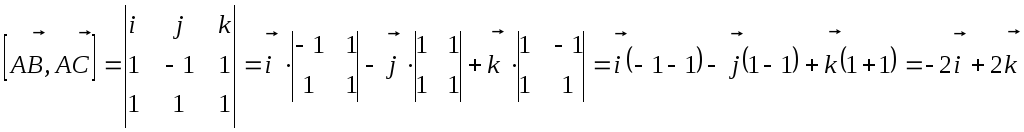 .
.
![]() .
.
![]() ,
,
![]() (ед2).
(ед2).
![]() (ед.).
(ед.).
