Глава 3. Квантовые статистические распределения.

§3.1. Статистическая сумма. Большой канонический ансамбль.

Известно, что все частицы в природе в зависимости от их спина делятся на фермионы и бозоны. Спин - это внутренний механический момент количества движения частицы не связанный с ее движением в пространстве. Частицы с полуцелым спином s = 1/2, 3/2, 5/2… называются фермионами, а частицы с целым значением s = 0, 1, 2, ... - бозонами. Так электрон, нейтрон, протон имеют s = 1/2 и являются фермионами. Бозонами являются фотон, векторные мезоны (s = 1) и гравитон (s = 2). В зависимости от спина, ядра атомов (и сами атомы) всех существующих в природе химических элементов тоже являются фермионами или бозонами. Различие между фермионами и бозонами заключается в возможности занимать одно и то же квантовое состояние нескольким тождественным частицам. Квантовые частицы неразличимы. Поэтому любые конфигурации, отличающимися только перестановками двух и более тождественных частиц считаются одинаковыми.

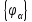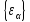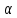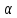Многочастичные квантовые состояния системы удобно записывать в представлении чисел заполнения. Для этого введем полный набор одночастичных состояний с собственными энергиями , где индекс- номер состояния. Многочастичное состояние определяется указанием числа частиц для всех значений . Числа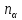принимают значения:

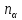=0,1,2,3, …. в случае статистики Бозе – Эйнштейна (Б-Э),

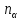= 0,1 - в случае статистики Ферми – Дирака (Ф-Д).

Одно из центральных мест в квантовой статистике занимает понятие статистической суммы (статсуммы)

. (3.1)

В этом выражении индекс n нумерует собственные функции |n> и собственные значения E_n всей системы. В квантовой статистике среднее значение оператора 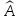в соответствии с распределением Гиббса определяется выражением

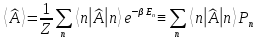, (3.2)

где 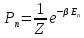– вероятность обнаружения системы в состоянии |n> . Если статсумма известна, то с её помощью можно найти все термодинамические свойства системы.

Введём свободную энергию

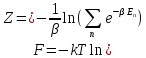(3.3)

и энтропию

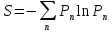. (3.4)

Определение энтропии (3.4) полностью соответствует определению, данному ранее в Главе 1. В условиях равновесия

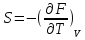. (3.5)

Использую нестационарную теорию возмущений легко показать, что при отклонении от равновесия энтропия с течением времени всегда возрастает

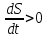. (3.6)

Рассмотрим полную энергию системы, находящейся в состоянии с номером n: 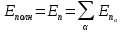, где 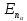- энергии подсистем. Тогда (=1/kT )

=

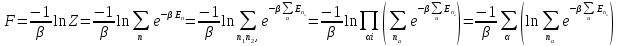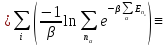(3.7)

Таким образом, свободная энергия всей системы есть сумма свободных энергий её подсистем.

При фиксированном числе частиц N в системе должно выполняться условие 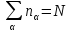, которое затрудняет вычисление статистической суммы. Данную проблему можно обойти, если ввести понятиехимического потенциала  для систем с переменным числом частиц. Ансамбль таких систем называется большим каноническим ансамблем. В этом ансамбле формально переходят к гамильтониану 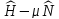. Химический потенциал находится из условия

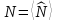и имеет смысл полной энергии, приходящейся на одну частицу.

В большом каноническом ансамбле статсумма равна

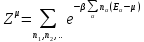. (3.8)

Свободная энергия 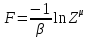называется термодинамическим потенциалом. В случае, когда,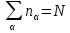

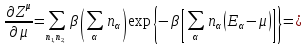
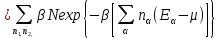. (3.9)

Однако, по определению,

,

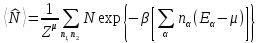так что 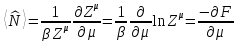.(3.10)

Последнее уравнение позволяет найти зависимость  от числа частиц .

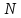Аналогичным образом можно получить:

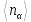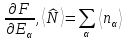= . (3.11)

Внутренняя энергия системы

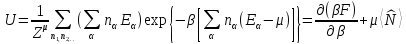. (3.12)

В качестве примера использования полученных выше формул рассмотрим одноатомный идеальный газ в трехмерном ящике с непроницаемыми стенками. Из квантовой механики известно, что энергия частиц равна

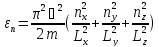, где размеры ящика, ацелые числа. Статистическую сумму запишем в видеZ=Z_x  Z_y  Z_z. Отдельные сомножители легко вычисляются:

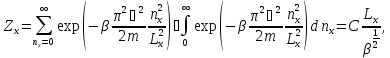
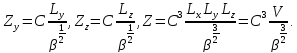
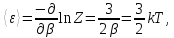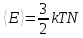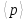Средняя энергия одной частицы равна а средняя энергия всех частиц . Используя полученные выражения для Z, можно найти среднее давление . Для этого примем во внимание, что

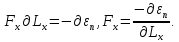
Тогда

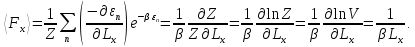
Отсюда получаем, что